Algoritmo per il calcolo di $P$

L'algoritmo per il calcolo della Presenza $P$ è il seguente:

   1.begin: 


2.		$D_{tot} = 0$ 


3.		For each category $c_i \in C$: 


4.				$D_i = 0$ 


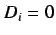
5.				For each document $d_{i,j} \in c_i$: 


6.						$D_{tot} = D_{tot}+1 , D_i = D_i+1$ 


7.						For each unique term $t \in d_{i,j}$: 


8.								If $t$ is $\in D_{i\vert t}$ then: 


9.										$D_{i\vert t} = D_{i\vert t}+1$ 


10.								else: 


11.										Add $D_{i\vert t} = 1$ 


12.								end if 


13.						end foreach 


14.				endforeach 


15.				For each term $t \in D_{i\vert t}$: 


16.						$P_{i\vert t} = \frac{D_{i\vert t}}{D_i}$ 


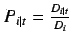
17.				end foreach 


18.		endforeach 


19.end 

Se si assume che si può usare una HashMap HM per conservare i risultati di $D_{i\vert t}$, in modo tale che ogni ricerca o aggiornamento in HM abbia un costo computazione costante pari a $k$, nel caso peggiore l'algoritmo per calcolare il parametro $P$ ha un costo di $O(C \cdot D \cdot T \cdot k)$. I simboli hanno i seguenti significati: $C$ è il numero di categorie, $D$ è il numero medio di documenti per ciascuna categoria, $T$ è il numero medio di termini per ciascun documento.