筆者在《廣義量詞系列:對偶性推理基礎》中介紹了當代「對偶性推理」 的基本原理。「對偶性推理」作為一種只有很短歷史的推理模式,本身沒有很豐富的內容,但經Keenan、 Westerstahl、Zuber等人的深入研究後,已發掘出很多新的內容。本文將主要介紹上述學者對此一課題的一些 研究成果,並加上筆者的一些個人研究成果。
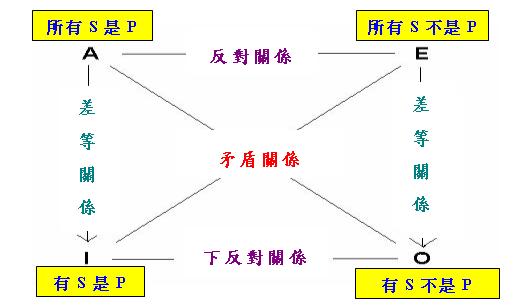
從某一角度看,上一章介紹的「外部否定」、「內部否定」和「對偶」概念是對傳統「對當關係推理」的一種 改造。「對當關係推理」是「古典形式邏輯」所研究的量化句推理的一種,古代學者把這種推理總結為以下的 「古典對當方陣」:

但正如筆者以往指出的,傳統「對當關係推理」中的「差等關係」之所以成立,其實依賴著一個「主語存在預 設」,即主語S是存在的。及至19世紀末和20世紀初,一些學者開始用數學方法研究邏輯,形成「現代數理邏輯 」。現代數理邏輯學家的研究對象雖然也包括量化句,但他們採用了全新的形式化表達方法,例如把「所有S是 P」和「有S是P」分別表達為
在這種新的表達法下,「主語存在預設」不再成立,導致傳統「對當關係推理」中的「差等關係」、「反對關 係」與「下反對關係」也不再成立,上述「古典對當方陣」退化為以下的「布爾對當方陣」:

筆者曾經指出,我們可以把「主語S存在」設定為上述「古典對當方陣」中四句共有的「預設」,這是保留「對 當關係推理」的一種方法。但除此以外,我們還有另一種改造「對當方陣」的方法,這就是把「古典對當方陣」 中的「矛盾關係」、「(下)反對關係」和「差等關係」分別改為前面介紹的「外部否定關係」、「內部否定關 係」和「對偶關係」。利用上述概念,當代的學者把「古典對當方陣」改造成以下的「新型對當方陣」 (有些人又稱「對偶方陣」Square of Duality):
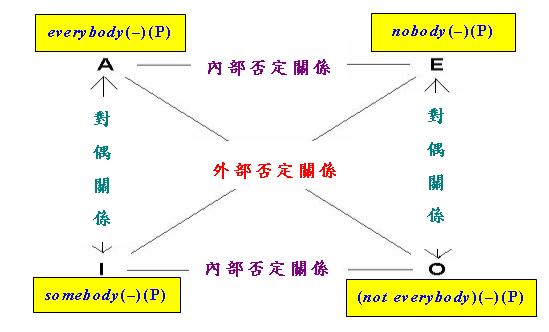
請注意上圖中的各種關係跟「古典對當方陣」中的關係具有不同的性質。舉例說,「全稱量詞」與「存在量詞」 在「差等關係」下本來是不對稱的:
但在「對偶關係」下卻變成對稱的:
由於「對偶關係」是對稱的,所以上圖中A與I句以及E與O句之間的箭頭是雙向而非單向的,而且「對偶關係」
的成立無需依賴「主語存在預設」(註1)。
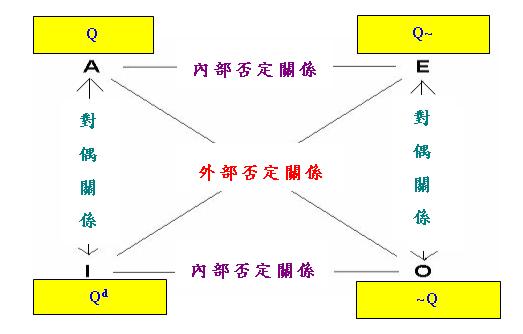
我們還可以把上述「新型對當方陣」推廣為更一般的形式:
「對偶性推理」並不局限於一般量詞,而是存在於很多語言結構中。舉例說,筆者在上一章便曾介紹四個「體 貌副詞」的各種否定關係,現在我們可以把這四個副詞排成以下「對當方陣」:
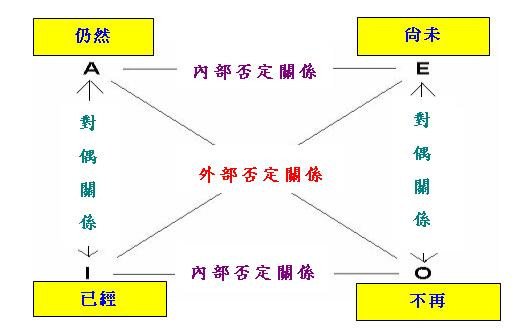
請注意上述副詞只適用於「新型對當方陣」而非「古典對當方陣」,這是因為「仍然」與「已經」之間並不存 在「差等關係」。由此可見,「新型對當方陣」中的推理關係的確超出了傳統「對當關係推理」的內容。
為了更簡潔地表達「新型對當方陣」,Peters和Westerstahl在Quantifiers in Language and Logic一 書中定義了一個函項Square (註2):設有「<1>型量詞」Q,則
例如
Peters和Westerstahl還證明了以下有關函項Square的定理。
| 定理1: | 以Square(Q)中任何一個元素作為Square的論元,所得 結果等於原來的Square(Q),即若Q' ∈ Square(Q),則Square(Q') = Square(Q)。 |
容易證明上述定理是正確的,只需把~Q、Q~和Qd逐個代入(1)即可。舉例說,
| Square(~Q) | = {~Q, ~(~Q), (~Q)~, (~Q)d} |
| = {~Q, ~~Q, ~Q~, ~~Q~} |
| = {~Q, Q, Qd, Q~} |
| = Square(Q) |
其餘有關Square(Q~)和Square(Qd)的計算也類此,這裡從略。
根據「定理1」,我們知道
現在我們以Q<1>代表由所有「<1>型量詞」組成的集合,那麼「定理1」告訴我們,如果我們把Q<1>中的元素逐 一代入(1),我們將得到Q<1>的一個「劃分」(Partition),即我們可以把Q<1>寫成
其中
根據集合論,每個Square(Qi)相當於Q<1>上的一個「等價類」(Equivalence Class),這些「等價 類」是由以下二元關係「*」導出的:
容易看到上述定義的「*」確是一個「等價關係」(Equivalence Relation)。
從「定理1」的證明中,容易看到「外部否定」、「內部否定」以及「對偶」運算(還可加上一個「恆等」
(Identity)運算,即把任何Q(#)(P)變成Q(#)(P)的運算)對於任意Square(Q)中的元素來說是封閉的。事實上,
從「群論」(Group Theory)的角度看,上述四個運算構成一個「克萊因4元群」(Klein 4-Group)。如果我們把
這四個運算看成這個群的元素,並把運算之間的「複合」(Composition) 看成這些元素之間的「乘法」(用。表
示),那麼我們有以下「乘法表」(以下用ID、IN、ON和DU分別代表「恆等」、「內部否定」、「外部否定」和
「對偶」):
| 。 | ID | IN | ON | DU |
|---|---|---|---|---|
| ID | ID | IN | ON | DU |
| IN | IN | ID | DU | ON |
| ON | ON | DU | ID | IN |
| DU | DU | ON | IN | ID |
由此可見,「新型對當方陣」具有深刻的集合論和群論意義。
筆者在上一章指出以下包含三層量詞的推理模式是有效的(在下式中,B代表「謂詞性論元」):
並指出上述推理模式實際上反映了「多重否定律」在下式中的運用:
請注意在上式中,置於中間的量詞Q'必須在上式右端轉化為~Q'~,才能剛好抵消處於其前及其後的兩個「~」。 如果在上式中,我們把Q'保持原狀不變,所得結果不是有效的推理模式:
這是因為在上式中,兩個「~」不能隔著中間的Q'而互相抵消。換句話說,在一般情況下,
不是有效的推理模式。
不過上述情況卻有一個例外,假如Q'(#')是本身的「對偶」,那麼(2)便是有效的推理模式。為此,我們需要引
入「自對偶」(Self-Dual)的概念:「<1>型量詞」Q(#)是「自對偶」的當且僅當
請注意根據Q(#)d的定義,我們可以把上式變換為
接下來的任務便是找出哪些「<1>型量詞」是「自對偶」的,即找出哪些量詞滿足(4)的等式。首先,我們知道 「專有名詞」滿足(4),這可以從以下等價關係看出:
以下給出一個形式證明。根據《廣義量詞系列:基本單式量詞》,我們可以 把「專有名詞」"John"表達為"every({j})",而"every({j})"的「外部否定」和「內部否定」 分別為"(not every)({j})"和"no({j})"。根據這兩個「<1>型量詞」的真值條件以及「單元集」 的性質,我們有
| (not every)({j})(B) | |
| ⇔ | {j} ∩ ~B ≠ Φ |
| ⇔ | {j} ⊆ ~B |
| ⇔ | {j} ∩ B = Φ |
| ⇔ | no({j})(B) |
由此證明了"every({j})"滿足(4)。請注意對於形如"every(A)" (其中A為任意集合)的量詞,上
述推理並不成立,因此一般的「全稱量化名詞組」不是「自對偶」的。
確立了「專有名詞」的「自對偶」性質,我們便可以構造一些涉及「專有名詞」的「對偶性推理」,例如我們
可以把「專有名詞」套用於上面(2)中的Q'(#'),從而得到以下推理實例:
其次,「反身代名詞」也是「自對偶」的。筆者在《廣義量詞系列:非迭代多式 量詞》中介紹了「普通反身化算子」和「領屬反身化算子」,以下只集中討論形式為 [self1(−)]2的「普通反身化算子」,這種「反身化算子」代表那些在 含有三元謂詞的句式中處於第二論元位置並且與第一論元同指的「反身代名詞」,例如"Every boy bought himself at most 3 gifts."中的"himself"。根據上述網頁,設B(x, y, z)為三元謂詞,那麼
如果我們把[self1(−)]2看作「<1>型量詞」,那麼我們可以仿照普通「 <1>型量詞」定義其「外部否定」和「內部否定」如下:
接著讓我們證明上述兩個集合是等價的。根據上述定義,對於任何(x, z)而言,我們有
| (x, z) ∈ [~self1(−)]2(B) | |
| ⇔ | (x, z) ∈ ~{(x, z): B(x, x, z)} |
| ⇔ | (x, z) ~∈ {(x, z): B(x, x, z)} |
| ⇔ | ~B(x, x, z) |
| ⇔ | (x, z) ∈ {(x, z): ~B(x, x, z)} |
| ⇔ | (x, z) ∈ [self1(−)]2(~B) |
| ⇔ | (x, z) ∈ [self1(−)~]2(B) |
由於(x, z)和B是任意的,我們證明了[~self1(−)]2 ≡ [self1(−)~]2,從而證明了 [self1(−)]2是「自對偶」的。請注意我們可以把上述證明推廣至其他 形式的「普通反身化算子」以及各種形式的「領屬反身化算子」。至此我們證明了普通格和所有格的「反身代 名詞」是「自對偶」的。把「反身代名詞」套用於(2)中的Q'(#'),我們可以得到以下推理實例:
最後,當n為奇數時,我們還可以構造一組形式為"(Q of the n)(A)"的「「自對偶部分格結構」,在這 裡「Q」代表一個數詞或多個數詞的析取,A則是「名詞性論元」。設|A| = n = 2k + 1,並設f為把{0, ... k} 映射到{0, 1}的函數,那麼我們可以定義以下「<1>型量詞」F(A):
| [F(A)](B) = | f(|A ∩ B|), | if 0 ≤ |A ∩ B| ≤ k | (5) |
| 1 − f(n − |A ∩ B|), | if k + 1 ≤ |A ∩ B| ≤ 2k + 1 |
由於把{0, ... k}映射到{0, 1}的函數共有2k+1個,當|A| = 2k + 1時,我們可以根據上式構造
2k+1個「<1>型量詞」。
接著讓我們看看上述量詞的一些實例。設n = 7 (即k = 3),並設f: 0 → 0, 1 → 0, 2 → 0, 3
→ 0,那麼根據(5),我們有以下「<1>型量詞」F1(A):
| [F1(A)](B) = | 0, | if 0 ≤ |A ∩ B| ≤ 3 |
| 1, | if 4 ≤ |A ∩ B| ≤ 7 |
請注意以上這個量詞可以表述為"(more than 3 of the 7)(A)",容易驗證這個量詞是「自對偶」的,
因為若在A的7個元素中,多於3個(即4至7個)不具有性質B,那麼必有0至3個元素具有性質B,亦即具有性質B的
元素的數目不多於3。換句話說,(more than 3 of the 7)(A)~ ≡ ~(more than 3 of the
7)(A)。
讓我們再看另一個例子。設n = 7,並設f: 0 → 0, 1 → 1, 2 → 1, 3 → 0,那麼根據(5)
,我們有以下「<1>型量詞」F2(A):
| [F2(A)](B) = | 1, | if |A ∩ B| ∈ {1, 2, 4, 7} |
| 0, | if |A ∩ B| ∈ {0, 3, 5, 6} |
請注意以上這個量詞可以表述為"(exactly 1 or 2 or 4 or all of the 7)(A)",容易驗證這個量詞也
是「自對偶」的,因為若在A的7個元素中,有1或2或4或7個不具有性質B,那麼必有6或5或3或0個元素具有性質
B,亦即具有性質B的元素的數目不是1或2或4或7。換句話說,(exactly 1 or 2 or 4 or all of the
7)(A)~ ≡ ~(exactly 1 or 2 or 4 or all of the 7)(A)。
在上述例子中,量詞"(exactly 1 or 2 or 4 or all of the 7)(A)"給我們提供了兩個集合:{1, 2,
4, 7}和{7 − 1, 7 − 2, 7 − 4, 7 − 7} = {6, 5, 3, 0},這兩個集合互斥,而且
這兩個集合的并集剛好等於{0, ... 7}。請注意上述例子的情況正是形式為"(Q of the n)(A)"的「自
對偶部分格結構」必須滿足的條件,即這類量詞必須能表述為"(exactly n1 or ...
nm of the n)(A)"的形式,其中{n1, ... nm}與{n −
n1, ... n − nm}互斥,而且這兩個集合的并集剛好等於{0, ... n}。根據上述
條件,我們知道只有在n為奇數的情況下,"(Q of the n)(A)"才可能是「自對偶」的。
接著讓我們證明在n為奇數的情況下,(5)所定義的量詞確是「自對偶」的。首先,由於[F(A)~](B) =
[F(A)](~B)以及A ∩ ~B = A − B,根據(5),我們有
| [F(A)~](B) = | f(|A − B|), | if 0 ≤ |A − B| ≤ k |
| 1 − f(n − |A − B|), | if k + 1 ≤ |A − B| ≤ 2k + 1 |
另一方面,由於n = 2k + 1 = |A| = |A ∩ B| + |A − B|,我們必有
因此我們可以把上式改寫為
| [F(A)~](B) = | f(n − |A ∩ B|), | if k + 1 ≤ |A ∩ B| ≤ 2k + 1 |
| 1 − f(|A ∩ B|), | if 0 ≤ |A ∩ B| ≤ k |
可是,上式正好是[~F(A)](B) = 1 − [F(A)](B)的定義,由此得~F(A) ≡ F(A)~,即這個量詞是「 自對偶」的。把前述的"(more than 3 of the 7)(A)"套用於(2)中的Q'(#'),我們可以得到以下推理實 例:
在本節我們探討另一種具有特殊性質的量詞。回顧上面的(3),如果我們把該等式中的Q(#)d改為 Q(#)~,我們將有一種新的關係:
我們把符合上述關係的「<1>型量詞」稱為「內部否定不動點」(Fixed Point with respect to Inner Negation)(註3)。根據上述定義,「內部否定不動點」Q(#)滿足以下推理模式:
但除此以外,「內部否定不動點」還可應用於包含兩層或三層量詞的推理中,只要把筆者在上一章介紹的某些 推理模式作適當修改便行了。舉例說,從以下推理模式
我們可以推導出「內部否定不動點」Q(#)滿足以下推理模式:
接下來的任務是找出各種「內部否定不動點」,即哪些「<1>型量詞」滿足(8)。Keenan在Further Excursions in Natural Logic: The Mid-Point Theorems一文中提出了以下的「中點定理」 (Mid-Point Theorem)。
| 定理2: | 設p、q為分數,其中0 ≤ p ≤ q ≤ 1並且p + q = 1,則「<1>型量詞」"(between p and q)(A)"和"(more than p but less than q)(A)"是 「內部否定不動點」。特別地,當p = q = 1/2時,p和q滿足上述條件,因此"(exactly half)(A)"也是 「內部否定不動點」。 |
請注意若p、q符合上述定理的條件,則1/2 − p = q − 1/2,即p和q離開[0, 1]的「中點」1/2的
距離相等,故此一定理稱「中點定理」。
以下用「反證法」來證明上述定理,為方便行文,以下設定|A ∩ B| / |A| = k,那麼根據集合論,|A
− B| / |A| = 1 − k。設p、q符合上述條件,並且(between p and q)(A)(B),即k
∈ [p, q]。現假設(between p and q)(A)(~B)不成立,即1 − k不在[p, q]之內,亦即1
− k < p或1 − k > q。由於p + q = 1,從上述結果我們可推得k > q或k < p,與k ∈ [p,
q]矛盾。由此證得(between p and q)(A)(B) ⇒ (between p and q)(A)(~B),同理亦易證
(between p and q)(A)(~B) ⇒ (between p and q)(A)(B)。綜合以上結果,我們證明了
"(between p and q)(A)"是「內部否定不動點」。只要把上述證明中的「閉區間」[p, q]換成「開區間
」(p, q),便可證明"(more than p but less than q)(A)"也是「內部否定不動點」。
請注意由於「部分格結構」也可看成某種「相對數量詞」,「中點定理」也適用於這類量詞,即設|A| = n,l
、m為自然數,0 ≤ l ≤ m ≤ n並且l + m = n,則"(between l and m of the n)(A)"和
"(more than l but fewer than m of the n)(A)"是「內部否定不動點」。利用「定理2」以及(9)-
(10),我們可以得到以下推理實例:
筆者在《廣義量詞系列:基本單式量詞》中介紹了「布爾量詞」的概念,即 用「(外部)否定」、「合取」和「析取」這三種「布爾運算」從較簡單量詞複合而成的量詞。根據Keenan和 Faltz合著的Boolean Semantics for Natural Language一書,「布爾運算」可以作用於多種語言結構, 而作用於不同結構上的「布爾運算」可能有不同的意義。對於「<1>型量詞」Q(#)和Q'(#')而言,上述三種「布 爾運算」的意義為:
我們有以下定理。
| 定理3: | 「內部否定不動點」在「布爾運算」下是封閉的,即 若Q(#)和Q'(#')是「內部否定不動點」,則~Q(#)、(Q(#) ∧ Q'(#'))和(Q(#) ∨ Q'(#'))也是「內部否 定不動點」。 |
以下讓我們證明上述定理。首先,設Q(#)為「內部否定不動點」,則有
| (~Q(#))~(B) | |
| ⇔ | (~Q(#))(~B) |
| ⇔ | ~(Q(#)(~B)) |
| ⇔ | ~(Q(#)~(B)) |
| ⇔ | ~(Q(#)(B)) |
| ⇔ | (~Q(#))(B) |
即~Q(#)也是「內部否定不動點」。其次,設Q(#)和Q'(#')為「內部否定不動點」,則有
| (Q(#) ∧ Q'(#'))~(B) | |
| ⇔ | (Q(#) ∧ Q'(#'))(~B) |
| ⇔ | Q(#)(~B) ∧ Q'(#')(~B) |
| ⇔ | Q(#)~(B) ∧ Q'(#')~(B) |
| ⇔ | Q(#)(B) ∧ Q'(#')(B) |
| ⇔ | (Q(#) ∧ Q'(#'))(B) |
即(Q(#) ∧ Q'(#'))也是「內部否定不動點」。同理亦易證(Q(#) ∨ Q'(#'))也是「內部否定不動點」
,「定理3」得證。
利用「定理3」,我們可以從已有的「內部否定不動點」推導出其他「內部否定不動點」。舉例說,根據「定理
2」,設0 ≤ p ≤ q ≤ 1並且p + q = 1,則"(between p and q)(A)"是「內部否定不動點」。
由於「內部否定不動點」在「(外部)否定」運算下封閉,由此可知上述量詞的「外部否定」"(more than q
or less than p)(A)"也是「內部否定不動點」。同樣,我們亦知道"(exactly half)(A) ∧
(between 4 and 6 of the 10)(B)"是「內部否定不動點」,因為此一量詞是兩個「內部否定不動點」
的「合取」。由此我們有以下推理實例:
Keenan在上述文章中還提出了以下的「廣義中點定理」(Generalized Mid-Point Theorem)。
| 定理4: | 設Q(#)為「<1>型量詞」,則「布爾量詞」(Q(#) ∧ Q(#)~)和(Q(#) ∨ Q(#)~)是「內部否定不動點」。 |
上述定理不難證明,設B為任意「謂詞性論元」,則有
| (Q(#) ∧ Q(#)~)~(B) | |
| ⇔ | (Q(#) ∧ Q(#)~)(~B) |
| ⇔ | Q(#)(~B) ∧ Q(#)~(~B) |
| ⇔ | Q(#)(~B) ∧ Q(#)(B) |
| ⇔ | Q(#)~(B) ∧ Q(#)(B) |
| ⇔ | (Q(#) ∧ Q(#)~)(B) |
即(Q(#) ∧ Q(#)~)是「內部否定不動點」,同理也易證(Q(#) ∨ Q(#)~)是「內部否定不動點」。
請注意在上述定理中,各個「布爾量詞」的兩個「名詞性論元」必須是同一個「#」,否則該定理不成立。但由
於「布爾運算」具有以下性質:
我們可以把這些量詞中的「布爾運算」從「<1>型量詞」的層面提升至「<1,1>型量詞」的層面。舉例說,我們
可以把"all boys or no boys"改寫為"all or no boys",即把這裡的"or"從連接兩個名詞短語的連詞提升為連
接兩個限定詞的連詞,以下筆者將採用這種方式處理這種「布爾量詞」。
利用「定理4」,我們可以發掘出更多「內部否定不動點」。舉例說,由於"(exactly q)(A)"與
"(exactly (1 − q))(A)" (其中q為分數)互為「內部否定」形式,我們知道"(exactly q or
(1 − q))(A)"是「內部否定不動點」。此一結果還可推廣至「部分格結構」,從而推知
"(exactly m or (n − m) of the n)(A)"也是「內部否定不動點」。我們有以下推理實例:
請注意在上述量詞中,q和(1 − q)離開1/2的距離以及m和(n − m)離開n/2的距離各自相等,所以
「定理4」稱為「廣義中點定理」。
我們還可以對上一章介紹的其他量詞綜合運用「定理3」和「定理4」,從而構造出各種「內部否定不動點」。
舉例說,我們可以根據「定理4」把互為「內部否定」的"all(A)"與"no(A)"組合成「內部否定
不動點」"(all or no)(A)",然後再應用「定理3」推知上述量詞的「外部否定」"(some but not
all)(A)"也是「內部否定不動點」。
請注意「定理4」只告訴我們理論上可以把哪些量詞配對,但實際上某些組合可能會產生「平凡量詞」。舉例說
,儘管"all(A)"與"no(A)"以及"some(A)"與"(not all)(A)"互為「內部否定」
形式,但在自然語言中卻不存在"(all and no)(A)"或"(some or not all)(A)"這樣的量詞,這
是因為這兩個量詞是「平凡量詞」:前者與任何「謂詞性論元」B結合後皆為假命題,相當於「永假量詞」
"0(A)";而後者與任何B結合後均為真命題,相當於「永真量詞」"1(A)" (註4)。
事實上,上述情況可以用「對當方陣」加以解釋。在「對當方陣」上,「內部否定」相當於兩種關係:「反對
關係」和「下反對關係」,這兩種關係分別為「不可同真」和「不可同假」的關係,因此若「<1,1>型量詞」Q
和Q'存在「反對關係」,則(Q ∧ Q')(A)相當於"0(A)";若Q和Q'存在「下反對關係」,則(Q ∨ Q')(A)
相當於"1(A)" (註5)。回顧「古典對當方陣」,我們看到"all"與"no"存在「反對關係」,而
"some"與"(not all)"則存在「下反對關係」,這就解釋了為何"(all and no)(A)"和
"(some or not all)(A)"相當於「平凡量詞」了。由此可見,在構造「內部否定不動點」時,除了應用
「定理4」外,我們還須應用「對當方陣」的知識,以避免構造出「平凡量詞」,這顯示現代的「對偶性推理」
與古典「對當關係推理」存在微妙的關係。
在本章和上一章,筆者介紹了「外部否定」和「內部否定」的概念(以及兩者的複合-「對偶」),這兩種否定
分別相當於筆者在《廣義量詞系列:單調性推理原理》中介紹的「算子否
定」和「論元否定」。對於「<1,1>型量詞」而言,「論元否定」可以作用於兩種對象。到目前為止筆者討論的
「內部否定」其實只相當於「右論元否定」。一個自然的推論是,是否可以把「左論元否定」引入「對偶性推
理」中?答案是肯定的。
為了區別兩種「論元否定」,由現在開始筆者將把此前討論的「內部否定」改稱為「右論元否定」
(Right-Argument Negation,又可稱為「謂語否定」);而把本節討論的否定稱為「左論元否定」
(Left-Argument Negation,又可稱為「主語否定」)。設有「<1,1>型量詞」Q,「左論元否定」就是把語句「
Q(A)(B)」變成「Q(~A)(B)」的變換(註6)。為簡化寫法,筆者將把Q的「左論元否定」記作Q~l (而
Q的「右論元否定」則記作Q~r,這裡下標中的"l"和"r"分別為"left"和"right"的縮寫),即
一般而言,我們可以在某一「<1,1>型量詞」的「名詞性論元」前加"non-" (相當於漢語的「非」)以得到該量 詞的「平凡左論元否定」形式。除此以外,在自然語言中某些「<1,1>型量詞」還具有「非平凡左論元否定」形 式。從直觀上看,只要我們把某一語句的兩個論元顛倒並把有關量詞換成其「逆向反義詞」,便可從「右論元 否定」得到「左論元否定」,例如我們可以把語句「every(A)(~B)」變換為「only(~B)(A)」。 由於根據上一章的表2,"every"與"no"互為「右論元否定」形式,即
而"no"具有「對稱性」,即
由此可得到
即"only"與"no"互為「左論元否定」形式。上述討論顯示,「非平凡左論元否定」形式可以從 某些「<1,1>型量詞」的「逆向反義詞」中尋。下表列出某些常用「<1,1>型量詞」的「逆向反義詞」及其真值 條件(在下表中,l、m、n為自然數,且0 < l < m < n,p、q為分數,且0 < p < q < 1,X代表「語境集」)(註 7):
| 論元結構 | 真值條件 |
|---|---|
請注意從語法上說,上表所列的量詞跟一般「<1,1>型量詞」不同,它們都不是「限定詞」,例如在傳統語法中
,"only"一般被分析為副詞,而"(constitute at least m of the n)"等則是「動詞 + 限定詞
」結構(筆者在這裡把「(constitute at least m of the n)(A)(B)」規定為語句"A constitutes at
least m of the n B."的論元結構)。不過,由於這些結構可作為某些常用「<1,1>型量詞」的「逆向反義詞」
出現於「對偶性推理」中,所以本文把這些結構處理成某種抽象的「<1,1>型量詞」。
根據上表,我們可以得到某些「<1,1>型量詞」的「非平凡外部否定」和「非平凡左論元否定」形式,如下表所
示:
| 量詞 | 「外部否定」形式 |
|---|---|
| 量詞 | 「左論元否定」形式 |
|---|---|
類似「右論元否定」,我們可以推導出涉及「左論元否定」的推理模式。根據「左論元否定」的定義,我們有 以下推理模式:
利用上述模式和表3,我們有以下推理實例:
我們能否把上述推理模式推廣為包含兩層量詞的「左論元否定」推理模式?回顧上一章,包含兩層量詞的「右 論元否定」推理模式都是涉及「迭代量詞」的推理,而「迭代量詞」的「迭代」運算都是作用於「右論元」上 ,例如以下語句
可以表達為以下「迭代」形式:
其中some(GIRL)(LOVE)處於外層「三分結構」的「右論元」位置。現在的問題是,哪一種語言結構可被 表達為作用於「左論元」上的「迭代」運算?答案就是某些帶有「定語分句」的語句。試看以下例句:
請注意上句存在岐義,這視乎"only"是以甚麼作為其焦點。假如上句的焦點結構如下所示(以下用[ ]F括出焦點):
即整個名詞短語"boys who love some girl"都在"only"的焦點內,那麼語句(12)的意思是:除了那些愛至少一 個女孩的男孩外,沒有其他個體(包括不愛任何女孩的男孩以及非男孩)出席。在這種解讀下,(12)應被表達為 以下「迭代三分結構」:
可是(12)還可以有另一種焦點結構,如下所示:
即只有關係分句"who love some girl"在"only"的焦點內。在這種焦點結構下,語句(12)的意思是:在男孩之 中,除了那些愛至少一個女孩的男孩外,沒有其他男孩出席,但並不排除有其他非男孩出席。以下筆者將主要 討論在第二種解讀下語句(12)的「對偶性推理」。現以下圖說明語句(12)的第二種解讀的意思:

在上圖中,L代表集合{x: some(GIRL)({y: LOVE(x, y)})},我們可以把(12)的第二種解讀視為陳述紅 色粗框包著的範圍(而非整幅圖)的情況,這相當於把(12)的論域從U縮小為BOY (即紅色粗框包著的範圍)。把論 域限制在BOY後,我們便可以把(12)的第二種解讀表達為
在上式中,"(onlyU|BOY)"表示對量詞"only"的「限制」(Restriction)操作,「限 制」操作的定義為:若Q為論域U上的「<1,1>型量詞」,S為任何集合,則
根據上述定義,"(onlyU|BOY)"的意思就是把"only"的論域從原來的U改為BOY,並 把BOY與"only"的原來兩個論元相交(這是要確保兩個新的論元為BOY的子集)。由於論域已改為BOY,因 此對(14)中的第一論元進行的否定運算也是相對於BOY而言的,即
| ~{x: some(GIRL)({y: LOVE(x, y)})} | |
| = | BOY ∩ ~{x: some(GIRL)({y: LOVE(x, y)})}} |
| = | BOY ∩ {x: no(GIRL)({y: LOVE(x, y)})}} |
| = | {x: no(GIRL)({y: LOVE(x, y)})}} |
把(14)應用於(11),我們便會得到以下與(14)等價的「三分結構式」:
由此得到以下推理實例:
仿照其他否定概念,我們也可以定義「左論元否定不動點」(Fixed Point with respect to Left-Argument Negation),這是指滿足以下條件的「<1,1>型量詞」Q:
根據上述定義,「左論元否定不動點」Q滿足以下推理模式:
接下來讓我們找出各種「左論元否定不動點」,即滿足(15)的「<1,1>型量詞」。由於「左論元否定」是「右論 元否定」的逆向反義概念,我們只要把第4節的「定理2」至「定理4」作適當修改,便可得到有關「左論元否定 不動點」的下列定理。
| 定理5: | 設p、q為分數,其中0 ≤ p ≤ q ≤ 1並且p +
q = 1,則「<1,1>型量詞」"(constitute between p and q)"和"(constitute more than p but
less than q)"是「左論元否定不動點」。特別地,當p = q = 1/2時,p和q滿足上述條件,因此
"(constitute exactly half)"也是「左論元否定不動點」。
|
| 定理6: | 「左論元否定不動點」在「布爾運算」下是封閉的,即若Q和Q'是
「左論元否定不動點」,則~Q、(Q ∧ Q')和(Q ∨ Q')也是「左論元否定不動點」。
|
| 定理7: | 設Q為「<1,1>型量詞」,則「布爾量詞」(Q ∧ Q~l)和(Q ∨ Q~l)是「左論元否定不動點」。 |
請注意「定理5」亦適用於「部分格結構」。利用上述定理,我們便可以構造出各種「左論元否定不動點」。舉 例說,根據「定理5」,我們推知"(constitute between 1/3 and 2/3)"是「左論元否定不動點」。根 據「定理7」和表3,我們推知"(only or no)"是「左論元否定不動點」;再根據「定理6」,可知上述 量詞的「外部否定」"(some but not restricted to)"也是「左論元否定不動點」(註8)。把上述量詞 應用於(16),便可得到以下推理實例:
我們還可以把"(only or no)"應用於包含兩層量詞的「左論元否定」推理中,例如
我們還可以繼續推廣上述否定概念,既然已有「右論元否定」和「左論元否定」的概念,那麼我們也可以定義 「左右論元否定」(Left and Right-Argument Negation,又可稱為「主謂否定」)的概念。以下筆者 把這種否定記作Q~lr,其定義如下:
根據上述定義,我們知道「左右論元否定」有以下推理模式:
自然語言中有哪些「<1,1>型量詞」具有「非平凡左右論元否定」形式?由於這種否定是「右論元否定」和「左 論元否定」的複合,我們可以從具有這兩種否定的「非平凡形式」的量詞中尋。根據表3,"only"和 "(apart from John only)"各有「非平凡左論元否定」形式,分別為"no"和"(no except John)";而根據上一章,這後兩個量詞又各有「非平凡右論元否定」形式,分別為"every"和 "(all except John)",由此我們得到以下結果:
| 量詞 | 「左右論元否定」形式 |
|---|---|
把上表所示量詞應用於(17),便可得到以下推理實例:
我們還可以構造包含兩層量詞的「左右論元否定」推理。舉例說,語句
可被表達為
把上式應用於(17),便可得到以下推理實例:
我們也可以定義「左右論元否定不動點」(Fixed Point with respect to Left and Right-Argument Negation)的概念,即滿足以下條件的「<1,1>型量詞」Q:
根據上述定義,「左右論元否定不動點」Q滿足以下推理模式:
由於「左右論元否定」是「右論元否定」和「左論元否定」的複合,容易看到這種否定也有類似「定理6」和「 定理7」的定理。
| 定理8: | 「左右論元否定不動點」在「布爾運算」下是封閉的,
即若Q和Q'是「左右論元否定不動點」,則~Q、(Q ∧ Q')和(Q ∨ Q')也是「左右論元否定不動點」。
|
| 定理9: | 設Q為「<1,1>型量詞」,則「布爾量詞」(Q ∧ Q~lr)和(Q ∨ Q~lr)是「左右論元否定不動點」。 |
利用「定理9」和表4,我們推知"(all and only)"是「左右論元否定不動點」;再根據「定理8」,可 知上述量詞的「外部否定」"(not all or not only)"也是「左右論元否定不動點」。以下僅舉涉及 "(all and only)"的一個推理實例:
「對偶」和「左右論元否定」是兩種否定的複合,前者是「外部否定」與「右論元否定」的複合,後者則是「 左論元否定」與「右論元否定」的複合。一個自然的推論是,應該還可定義其他複合否定概念。首先,我們可 以把「外部否定」與「左論元否定」複合,從而得到一種新的「對偶」。為區別新舊兩種「對偶」,現把此前 介紹的「對偶」改稱「右對偶」(Right Dual),並把本小節介紹的「對偶」稱為「左對偶」 (Left Dual),記作Qld (而Q的「右對偶」則記作Qrd),其定義為
根據上述定義,「左對偶」有以下推理模式:
接著我們可以利用表2和表3求得某些量詞的「非平凡左對偶」形式:
| 量詞 | 左對偶 |
|---|---|
利用上表,我們可以得到以下推理實例:
類似第3節介紹的「自對偶」(以下改稱「右自對偶」Right Self-Dual),我們也可定義「左自 對偶」(Left Self-Dual)的概念,即滿足以下條件的「<1,1>型量詞」Q:
根據上述定義,「左自對偶」量詞Q滿足以下推理模式:
請注意我們可以沿用3.2.3小節的公式(5)以得到形式為"(constitute Q of the n)"的「左自對偶」量 詞,只要把該公式中A和B的角色對調便行了。根據3.2.3小節的討論,我們知道"(constitute more than 3 of the 7)"是「左自對偶」量詞,從而有以下推理實例:
其次,我們可以把三種否定(「外部否定」、「左論元否定」和「右論元否定」)複合,筆者把這種複合稱為 「左右對偶」(Left and Right Dual),記作Qlrd,其定義為
根據上述定義,「左右對偶」有以下推理模式:
鑑於此一概念涉及三重否定,在自然語言中究竟是否有量詞具有「非平凡左右對偶」形式?根據表4, "every"與"only"互為「左右論元否定」形式,由此可以求得這兩個量詞的「左右對偶」為:
| 量詞 | 左右對偶 |
|---|---|
但問題是,此前筆者一直不把"(not all)"和"(not only)"視作「非平凡外部否定」形式,因此 嚴格地說,自然語言中沒有量詞具有「非平凡左右對偶」形式。不過即使如此,也不阻礙我們進行「左右對偶」 推理,例如:
接著我們研究哪些量詞是「左右自對偶」(Left and Right Self-Dual)量詞,即滿足以下條件的「<1,1>型量詞 」Q:
首先,從表6可見,只有極少量詞具有「非平凡左右對偶」形式,而且這些量詞都不是「左右自對偶」量詞。
其次,對於「左右對偶」運算來說,沒有類似「定理4」的定理,即對表6的量詞進行「布爾運算」,也不能得
到「左右自對偶」量詞。由此可以推斷,自然語言中不存在「左右自對偶」量詞。
最後,筆者還要指出,「外部否定不動點」(Fixed Point with respect to Outer Negation)也是不存在的。
「外部否定不動點」是指滿足以下條件的「<1>型量詞」Q(#):
以下讓我們用「反證法」來證明沒有量詞可滿足上述條件,故設存在這樣的量詞Q(#),那麼對於任何「謂詞性 論元」B,都有
但上式是不可能成立的,因為任何命題「Q(#)(B)」都不可能與其否定命題等價。
至此筆者已把上一章介紹的三種否定運算擴充為七種,現把這七種否定運算(另加一個「恆等」運算)的定義總 結成下表:
| 運算 | 定義 | ||
|---|---|---|---|
| 量詞 | 左論元 | 右論元 | |
理論上,給定一個「<1,1>型量詞」Q,我們可以找出與Q相應的七個否定形式。舉例說,給定"every", 我們除了可找出上一章已介紹的三種相應否定形式(即「右論元否定」形式"no"、「外部否定」形式 "(not every)"和「右對偶」形式"some"外,我們還可以找出其餘四種否定形式,即「左論元否 定」形式"(every non-)"、「左右論元否定」形式"only"、「左對偶」形式"(not every non-)"和「左右對偶」形式"(not only)"。請注意上面列舉的量詞有一些不太自然或一般不被看作 一個語言單位,例如"(every non-)"。不過為了使本節的討論完整,這裡姑且把這些詞項當作普通「 <1,1>型量詞」處理。事實上,這些詞項像其他量詞一樣具有明確的真值條件,例如"(every non-)"的 真值條件就是:
利用"every"以及上述七個否定形式,我們便可以把前述的「新型對當方陣」擴大為以下的「對當 立方體」(Cube of Opposition)(註9):

上圖沒有列出立方體中每一對頂點之間的關係,這是因為該立方體的八個頂點共可構成C(8, 2) = 28個對子, 如果把這28個對子的關係全部列於上圖,將使上圖非常雜亂。不過要推導這28個關係其實不難,首先我們像上 面2.2小節那樣構造上述八種運算之間的「乘法表」(以下用ID、RN、ON、RD、LN、LRN、LD和LRD分別代表「恆 等」、「右論元否定」、「外部否定」、「右對偶」、「左論元否定」、「左右論元否定」、「左對偶」、「 左右對偶」):
| 。 | ID | RN | ON | RD | LN | LRN | LD | LRD |
|---|---|---|---|---|---|---|---|---|
| ID | ID | RN | ON | RD | LN | LRN | LD | LRD |
| RN | RN | ID | RD | ON | LRN | LN | LRD | LD |
| ON | ON | RD | ID | RN | LD | LRD | LN | LRN |
| RD | RD | ON | RN | ID | LRD | LD | LRN | LN |
| LN | LN | LRN | LD | LRD | ID | RN | ON | RD |
| LRN | LRN | LN | LRD | LD | RN | ID | RD | ON |
| LD | LD | LRD | LN | LRN | ON | RD | ID | RN |
| LRD | LRD | LD | LRN | LN | RD | ON | RN | ID |
利用上表,我們便可以推導上圖中任何一對頂點之間的關係。舉例說,由於"no"與"(not
only)"分別為"every"的「右論元否定」(RN)和「左右對偶」(LRD)形式,根據上表,LD。RN = LRD
並且LD。LRD = RN,這即是說,當我們把「no(A)(B)」變換為「~no(~A)(B)」後,便會得到
「(not only)(A)(B)」,反之亦然。由此可知,"no"與"(not only)"之間存在「左對偶
」關係。
理論上,我們還可以仿照2.2小節所介紹的,定義一個函項Cube:設有「<1,1>型量詞」Q,則
例如
當然,在自然語言中我們不容易找到齊備上列八個形式的「<1,1>型量詞」,因此上述函項一般只有理論意義, 筆者不擬深入討論。
到目前為止,筆者所介紹的「對偶性推理」都是「直接推理」,即從一個前提直接推出結論的推理。Keenan在
Excursions in Natural Logic一文中提出了一個定理,涉及由兩個前提推出結論的推理模式,後來
Westerstahl改良了這個定理,現把這個定理引述如下。
定理10:設Q為「右守恆」的「<1,1>型量詞」,則Q是「右遞增」的當且僅當以下推理成立:
| 前提1: | Q(A)(B) | (24) (註10) |
| 前提2: | Q(A)d(C) | |
| 結論: | some(A)(B ∩ C) |
筆者把上述推理模式稱為「對偶三段論」,以下是上述推理模式的一個實例(請注意"(more than 2/3)"是「右守恆」和「右遞增」量詞):
| 前提1: | 超過三分二會員出席了會議。 |
| 前提2: | 至少三分一會員是女性。 |
| 結論: | 有會員是女性且出席了會議。 |
上述定理須用到「右守恆性」和「右遞增性」的概念,其中「右遞增性」以及下文將須用到的「左遞增性」在 《廣義量詞系列:單調性推理原理》中已有所介紹。至於「右守恆性」以 及下文將會介紹的「左守恆性」,這裡只提供簡單定義,筆者以後還會詳細討論這兩種性質。設Q為「<1,1>型 量詞」,A、B為集合,則Q是「右守恆」(Right Conservative)的當且僅當
Q是「左守恆」(Left Conservative)的當且僅當
接著讓我們證明上述定理。首先設Q為「右遞增量詞」,並且Q(A)(B)和Q(A)d(C)真,我們用「反證
法」來證明some(A)(B ∩ C)也真,故設此一結論不真,即A ∩ B ∩ C = Φ,則有A
∩ B ⊆ ~C。從Q的「右守恆性」以及Q(A)(B),可推得Q(A)(A ∩ B)真。再根據Q的「右遞增性」,
必有Q(A)(~C)真,即~(Q(A)(~C))假。但~(Q(A)(~C)) ≡ Q(A)d(C),即Q(A)d(C)
假,這與前面的假設矛盾,由此我們證明了Q為「右遞增量詞」 ⇒ (24)有效。
其次設(24)為有效推理模式,並且B ⊆ B'和Q(A)(B)真,我們用「反證法」來證明Q(A)(B')也真,故設此
一結論不真,則有Q(A)~(~B')假,即~(Q(A)~(~B'))真,但~(Q(A)~(~B')) ≡ Q(A)d(~B')。
從(24)以及Q(A)(B)和Q(A)d(~B'),我們可以推出some(A)(B ∩ ~B'),即A ∩ B
∩ ~B' ≠ Φ。由此得B ∩ ~B' ≠ Φ,但這與B ⊆ B'矛盾。由此我們證明了(24)有效
⇒ Q為「右遞增量詞」。綜合以上結果,「定理10」得證。
根據對稱性,我們還可以得到以下這個涉及「左對偶」的定理。
定理11:設Q為「左守恆」的「<1,1>型量詞」,則Q是「左遞增」的當且僅當以下推理成立:
| 前提1: | Q(A)(B) | (25) |
| 前提2: | Qld(C)(B) | |
| 結論: | some(A ∩ C)(B) |
上述定理的證明跟「定理10」大同小異,只須把該定理中的「右」改為「左」便行。以下是上述推理模式的一 個實例例(請注意"only"是「左守恆」和「左遞增」量詞):
| 前提1: | 只有會員出席了會議。 |
| 前提2: | 有女性出席了會議。 |
| 結論: | 有女會員出席了會議。 |


