筆者在《廣義量詞系列:古典推理模式》中介紹了三種與量詞有關的古典
推理模式,包括兩種「直接推理」-「對當關係推理」和「結構變換推理」以及一種「間接推理」-「三段論
推理」。儘管在現代數理邏輯興起後,這些推理模式都退居次要地位,但隨著「廣義量詞理論」的發展,由於
這些推理模式與量詞有密切關係,這些推理又重新成為某些學者研究的對象,並從而獲得新生。在本章,筆者
將主要介紹「直接推理」在當代的革新,有關「三段論推理」的革新將留待以後再介紹。
其實在上一章,筆者已揭示了擴大「直接推理」內容的可能性。舉例說,筆者在該章顯示了,我們可以把「古
典對當方陣」擴大應用於含有量詞"only"的語句。此外,筆者還把「對當關係推理」和「結構變換推理
」應用於「個體論域」以外的多種論域,從而發掘出多種前人沒有研究過的推理模式,或對某些散見於不同邏
輯分支部門的推理模式給予了一種統一的解釋。因此上一章實質上已超越了古典形式邏輯的框框,在本章筆者
將循其他方向擴大「直接推理」的內容,其中一個方向就是把這種推理推廣至其他量詞。
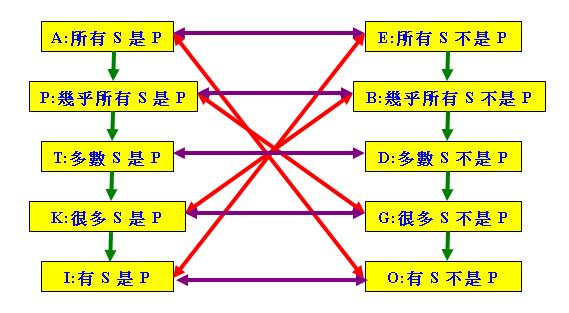
Peterson在Intermediate Quantifiers – Logic, linguistics, and Aristotelian semantics一書中 把三個介乎傳統量詞"all"和"some"的「中間量詞」(Intermediate Quantifier)(註1)- "(almost all)" (相當於漢語的「幾乎所有」)、"most" (相當於漢語的「多數」)和 "many" (相當於漢語的「很多」)加入到「古典對當方陣」中,從而得到以下的「五層對當方陣」:

為了方便稱呼上述方陣中的六個新語句,Peterson採用三個「清塞音」(Voiceless Stop)字母P、T和K分別稱呼
上圖中左排的三個新語句,並用三個「濁塞音」(Voiced Stop)字母B、D和G分別稱呼上圖中右排的三個新語句
,以區別於「古典對當方陣」原有的四個以元音字母A、E、I和O命名的語句。
請注意上述「對當方陣」仍然體現了傳統的「對當關係」,其中綠色單向箭頭代表「差等關係」,紅色雙向箭
頭代表「矛盾關係」,紫色雙向箭頭則代表「(下)反對關係」(位於上方的三個紫色箭頭代表「反對關係」,其
餘的兩個箭頭則代表「下反對關係」)。不過,上述方陣的「對當關係」比「古典對當方陣」豐富複雜得多。事
實上,上圖遠未能概括方陣中的所有「對當關係」。舉例說,「差等關係」便不只上圖所示的8個,其實左右兩
排中處於較高位置的語句都與位於其下的每一個語句存在「差等關係」,例如P句便與T句、K句和I句存在「差
等關係」。「(下)反對關係」也非只圖中所示的5個,而是有更多。例如O句便與P句存在「下反對關係」,這是
容易證明的。首先,這兩句顯然可以同真,但它們不可同假,因為若O句假,那麼根據O句與A句的「矛盾關係」
,必有A句真;而根據A句與P句的「差等關係」,必有P句真,由此可知O句與P句存在「下反對關係」。
正如在「古典對當方陣」中,E句有一個變體:「沒有S是P」一樣,上述方陣中的P和B句也各有一個變體:「很
少S不是P」和「很少S是P」(這裡的「很少」相當於英語的"few")。事實上,Peterson正是以這個變體作為兩個
新增「矛盾關係」(P與G句、B與K句的「矛盾關係」)的依據,因為在自然語言中,「很多」和「很少」正好構
成一對相反詞,這樣G與P句的「矛盾關係」便可透過以下關係推得:
當然,在自然語言中介乎"all"和"some"的量詞絕非只上述這些,因此我們還可以循其他途徑擴
充「古典對當方陣」。事實上,Peterson在他的書中便研究了各種「數量比較算子」,包括「分數量詞」
(Fractional Quantifier),例如"(more than 2/3)"、「複雜分數量詞」(Complexly Fractionated
Quantifier),例如"(much more than 2/3)",並嘗試用這些量詞構成比上述方陣更複雜的「對當方陣
」,即「多層對當方陣」。Peterson亦初步探討了用「關係命題」(Relational Statement)構造「對
當方陣」的問題(註2)。
總上所述,Peterson的研究大大擴展了「對當關係推理」的內容,他所研究的「中間量詞」已涵蓋多種「廣義
量詞」,包括「數量比較算子」、「模糊量詞」、「迭代量詞」等。不過,Peterson在處理「中間量詞」的定
義和推理時,沒有使用「廣義量詞理論」或「模糊數學」的形式化方法,而是根據一般人對這些量詞語義的直
觀理解,因此上述「對當方陣」中的推理關係便缺乏理據,難以再作進一步的推廣。
以下筆者將從另一角度探討如何擴充「古典對當方陣」的問題,首先討論「數量比較算子」。「多於 」、「少於」、「至少」和「最多」是進行數量比較的四個最基本的算子,在數學上分別用符號「>」、「<」 、「≥」和「≤」表示。在初等數學中我們便已學到這四個算子之間的關係,例如「>」蘊涵「≥」,「 <」的否定是「≥」等等。不難發現,這四個算子之間的關係完全符合「古典對當方陣」中的關係,所以我們 可以把這些關係表達成以下這個「數量比較對當方陣」:
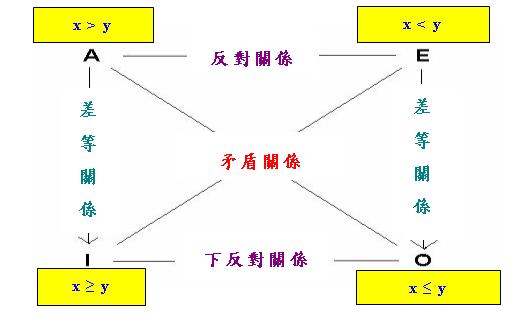
讀者可自行驗證上述方陣中各個關係的有效性。舉例說,A和E兩句顯然不可同真,但可同假。令這兩句同假的
情況就是x = y,此一情況亦可用來作為I和O兩句可同真的例證。
請注意以上方陣的四個語句代表一個抽象模式,可表達自然語言中的多種句式。這裡的x和y是兩個數量,在不
同場合,它們可體現為不同的數值。舉例說,當x和y分別是整數5和3 時,上述方陣的A句便代表數學不等式「5
> 3」。當x是「穿校服的學生人數」,y是數字3時,A句便代表「超過三名學生穿校服」。當x是「正在玩耍的
兒童人數」,y是數字1 時,A句便代表「有些兒童在玩耍」。當x是「穿校服的學生人數」,y是「不穿校服的
學生人數」時,A句便代表「多數學生穿校服」。當x是「John的高度」,y是「1.8米」時,A句便代表「John的
高度高於1.8米」。當x是「John喝了的水佔全部水的比率」,y是分數1/3時,A句便代表「John喝了超過三分一
水」。當x是「John的可靠程度」,y是「Mary的可靠程度」時,A句便代表「John較Mary可靠」。不僅如此,上
述四個「數量比較算子」在不同場合中還可體現為多種不同的詞語,充分顯示自然語言的多樣性,例如「多於」
便可表達為「超過」、「大於」,「至少」可表達為「不少於」、「多於或等於」等。
利用上述方陣,我們可以發掘和解釋多種涉及數量比較的推理。舉例說,根據E和I句的「矛盾關係」,可以推
得以下等價語句:
在上述「對當方陣」中,「數量比較算子」直接用於兩個實數之間的比較,但「數量比較算子」也可作為量詞 的一部分,例如出現於「多於n%」、「至少n%」等量詞中。以下就是由「多於n%的S是P」等語句構成的「 數值對當方陣(第一型)」:
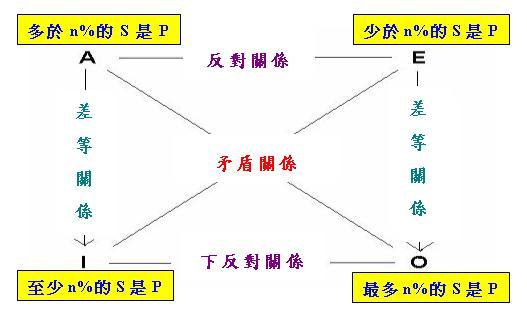
請注意在上述方陣中,n不論取開區間(0, 100)內任何數值,方陣中各關係都成立。
以上對當方陣可以有多種變體。舉例說,我們可以把上述方陣中的百分數「n%」改為分數「m/n」或整數「m個」
。我們也可以把方陣中的「<1,1>型量詞」改為「結構化量詞」,例如把方陣中的A、E、I和O句分別改為英語的
"More S than T are P."、"Fewer S than T are P."、"At least as many S as T are P."和"At most as
many S as T are P.",從而構成形式上更複雜的「對當方陣」。
有些人可能覺得以上方陣跟「古典對當方陣」在形式上有異,因為「古典對當方陣」的A和E句分別為「所有S是
P」和「所有S不是P」,即E句是把A句的系詞「是」改為「不是」而成,I與O句之間的關係也是如此。但在上述
方陣中,E句「少於n%的S是P」無論在形式上或語義上都並不等同於「多於n%的S不是P」,O句「最多n%的S是P」
也不等同於「至少n%的S不是P」(除非n剛好等於50)。筆者認為「對當方陣」的本質不是方陣中四個語句的形式
,而是這些語句之間的邏輯關係。只要有關語句符合「對當關係」,便可把它們構成「對當方陣」,而無需拘
泥於這些語句的形式。
當然,只要運用一些數學知識,我們也可以把上述方陣改造成與「古典對當方陣」相似的形式。以下筆者就構
造一個A和E句分別為「多於n%的S是P」和「多於n%的S不是P」的「對當方陣」。由於「多於n%的S不是P」在邏
輯上等同於「少於(100 − n)%的S是P」(請讀者自行驗證這一點),而I句與E句須處於「矛盾關係」,這
個方陣的I句便只能是「少於(100 − n)%的S是P」的否定,即「至少(100 − n)%的S是P」。基於相
同的推理,我們可以確定這個方陣的O句必須是「至少(100 − n)%的S不是P」。這樣我們便得到以下這個
「數值對當方陣(第二型)」:
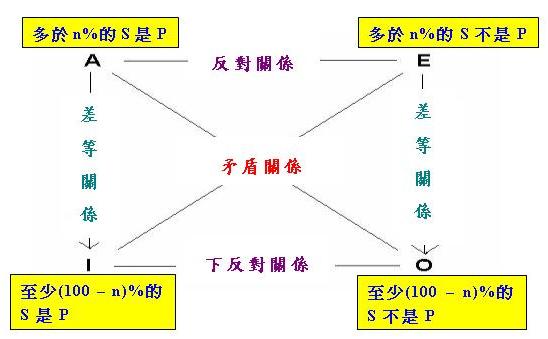
上述第二型方陣跟第一型有所不同,那就是方陣中的n必須滿足條件50 ≤ n < 100,否則方陣中的「(下)反
對關係」不成立(請讀者自行驗證這一點)。容易驗證上述方陣中各個關係的有效性。舉例說,由於根據上述條
件,n%大於或等於半數,所以A與E句不可能同真,但卻可同假。令這兩句同假的情況就是「50%的S是P」(亦即
「50%的S不是P」),此一情況亦可用來作為I和O兩句可同真的例證。
同樣,以上對當方陣也可以有多種變體。例如我們可以把上述方陣中的百分數「n%」和「(100 − n)%」
分別換成分數「m/n」和「1 − m/n」,惟m/n必須滿足條件1/2 ≤ m/n < 1。如果主語S的總數(即|S|)
是語境中的已知信息或話語中的給定信息,我們還可以把以上方陣中的百分數「n%」和「(100 − n)%」
分別換成整數「m個」和「|S| − m個」,惟m必須滿足條件|S| / 2 ≤ m < |S| (若|S|是偶數)或(|S|
+ 1) / 2 ≤ m < |S| (若|S|是奇數)。舉例說,如果|S| = 30,那麼可以設m = 16。相應地,以上方陣中的
A、E、I和O句便分別變成"More than 16 of the 30 S are P."、"More than 16 of the 30 S are not P."、
"At least 14 of the 30 S are P."和"At least 14 of the 30 S are not P."。上述最後一種變體可用來表
達自然語言中某些涉及「部分格結構」的推理,例如:
綜合上一章和本章的討論,我們看到「對當關係」不僅存在於古典形式邏輯所研究的「古典對當方陣」中,而
且存在於多種語言結構中,包括包含量詞"only"的語句以及包含各種「數量比較算子」的語句。據此我
們可以構造出多種在形式上與「古典對當方陣」有所不同的「對當方陣」。現在的問題是,我們能否從這些表
面上各不相同的「對當方陣」中總結出一般的規律,從根本上揭開「對當關係推理」的奧秘?
其實,只要細心比較一下兩個最典型的「對當方陣」,即「古典對當方陣」以及上一小節介紹的「數量比較對
當方陣」,便能發現兩者之間的共通點。首先看看兩個方陣中A與I句的「差等關係」何以能成立。容易看到,
在「數量比較對當方陣」中,I句「x ≥ y」可以被拆解成「x > y或x = y」,因此I句根本包含著A句「x >
y」的意思。同樣,在「古典對當方陣」中,I句「有S是P」可以被拆解成「所有S是P或部分S是P」,因此I句根
本包含著A句「所有S是P」的意思。以上就是在上述兩個方陣中A句蘊涵I句而I句卻不蘊涵A句的根本原因,上述
分析亦適用於E與O句的「差等關係」。
其次看看兩個方陣中I與E句的「矛盾關係」何以能成立。如此所述,在「數量比較對當方陣」中,I句可以被拆
解成「x > y或x = y」,而根據數學上的「實數三分律」(Trichotomy Law for Real Numbers),任何兩個實數
x與y之間有且只有下列三種關係之一成立:x > y、x = y 和x < y。因此若果「x > y或x = y」(即I句)假,必
有「x < y」(即E句)真,反之亦然。同樣,在「古典對當方陣」中,I句可以被拆解成「所有S是P或部分S是P」
,而在集合論上,就集合A而言,其元素屬於集合B的情況有且只有下列三種可能性之一成立:「所有A都是B」
、「部分A是B」和「沒有A是B」,這裡同樣存在一個「三分關係」。因此若果「所有S是P或部分S是P」(即I句)
假,必有「沒有A是B」(即E句)真,反之亦然。以上就是在上述兩個方陣中I與E句矛盾的根本原因,上述分析亦
適用於A與O句的「矛盾關係」。
至此我們看到了「對當方陣」的奧秘其實在於方陣中的I句可被拆解成包含A句意思的「析取式」,而這個「析
取式」中的兩項又與E句剛好構成一種「三分關係」。與此同時,方陣中的O句可被拆解成包含E句意思的「析取
式」,而這個「析取式」中的兩項又與A句剛好構成一種「三分關係」。現在如果我們用p、q、r代表上述「三
分關係」中的三個命題,這三個命題合起來窮盡一切可能性(Collectively Exhaustive)並且兩兩互斥
(Mutually Exclusive),用邏輯符號表達就是p ∨ q ∨ r 並且~(p ∧ q) ∧ ~(q ∧ r) ∧
~(r ∧ p),那麼「對當方陣」中的A、E、I和O句便可以分別表述為p、r、p ∨ q和r ∨ q。換句話說
,我們有以下的「對當方陣一般模式(第一形式)」:
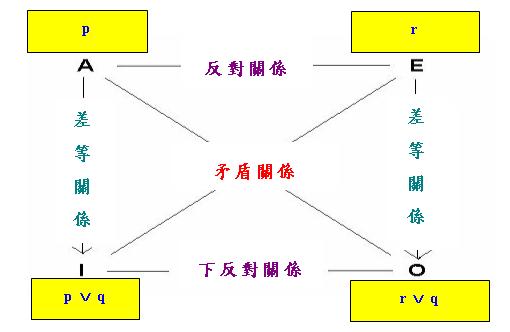
根據前面的討論,上述方陣中的「差等關係」和「矛盾關係」都是有效的,容易驗證以上方陣中的「(下)反對 關係」也是有效的。舉例說,根據p、q、r的互斥性,A和E兩句不可同真,但可同假。令這兩個命題同假的情況 就是q真,此一情況亦可用來作為I和O兩句可同真的例證。
「對當方陣」還可以總結為另一種一般形式。現設有兩個命題s和t滿足「單向蘊涵關係」:s ⇒ t ∧ t ~⇒ s,那麼我們可以把s、~s、t和~t排成以下的「對當方陣一般模式(第二形式)」:

讀者不妨自行驗證上述方陣中各個關係的有效性,「差等關係」和「矛盾關係」顯然成立,「(下)反對關係」
的有效性也容易驗證。舉例說,A和E兩句不可同真,這是因為若s真,那麼根據「差等關係」必有t真,這與~t
矛盾;但上述兩句可同假,令這兩句同假的情況就是s假且t真,請注意此一情況正是令I和O兩句同真的情況。
「對當方陣一般模式」兩種形式的差異在於,「第一形式」乃基於某種「三分關係」,而「第二形式」則是基
於某種「單向蘊涵關係」,不過這兩種形式其實是可以相互轉化的。首先,給定「對當方陣一般模式(第一形式
)」,我們有三個處於「三分關係」的命題p、q和r。現在如果我們設定s = p和t = p ∨ q,那麼s ⇒ t
∧ t ~⇒ s,並且根據「三分關係」的定義,我們有~t = r和~s = r ∨ q,由此便得到「對當方陣
一般模式(第二形式)」。
反過來,給定「對當方陣一般模式(第二形式)」,我們有「單向蘊涵關係」:s ⇒ t ∧ t ~⇒ s
,那麼必有以下「三分關係」:t ∧ s、t ∧ ~s和~t,容易證明(例如用「真值表法」)上述三個命題滿
足「三分關係」的定義。現在如果我們設定p = t ∧ s、q = t ∧ ~s和r = ~t,便可得到「對當方陣一
般模式(第一形式)」。由此可見,只要存在一個「三分關係」或「單向蘊涵關係」,我們便能構造相應的「對
當方陣一般模式」的第一或第二形式,而且這兩種形式是可以相互轉化的。
「對當方陣一般模式」的意義在於,以明晰的邏輯語言揭示了「古典對當方陣」以及本文介紹的其他「對當方
陣」的統一理據。不僅如此,「對當方陣一般模式」還可幫助我們發掘並解釋更多前人未有發現的「對當關係
推理」,從而大大豐富此一推理的內容。在本節的其餘部分,筆者將討論「對當方陣一般模式(第一形式)」和
「對當方陣一般模式(第二形式)」(以下分別簡稱「第一形式」和「第二形式」)的應用。
首先回顧上文2.2小節介紹的「數值對當方陣(第一型)」。容易看到如果我們把「第一形式」中的p、q和r分別
定為「多於n%的S是P」、「剛好n%的S是P」和「少於n%的S是P」,便可得到上述方陣。由於上述三個命題顯然
滿足「三分關係」的定義,我們看到上述方陣其實只是「第一形式」的特例。請注意由於在「第一形式」中,q
被「融入」於I (p ∨ q)和O (r ∨ q)句中,所以上述方陣並無「剛好n%的S是P」這樣的語句。可是,上
述p、q和r與三個命題的對應關係不是絕對的,假如現在我們想研究量詞"(exactly n%)" (即漢語的「
剛好n%」)的「對當關係推理」,那麼只要重新調配上述對應關係,便可以構造一個含有「剛好n個」的「對當
方陣」。具體地說,如果現在我們把p、q和r分別定為「剛好n%的S是P」、「多於n%的S是P」和「少於n%的S是P
」,便可構造如下的「對當方陣」:
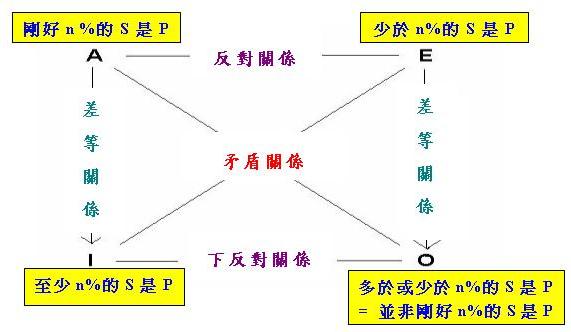
其次回顧2.2小節介紹的「數值對當方陣(第二型)」。經過仔細推敲後,應能看到如果我們把p、q和r分別定為
「多於n%的S是P」、「介乎(100 − n)%和n%的S是P」和「少於(100 − n)%的S是P」,便可得到上
述方陣。容易看到上述三個命題只有在滿足條件n ≥ 50時才構成「三分關係」,這是因為如果n < 50,那麼
必有100 − n > n,這時「多於n%的S是P」和「少於(100 − n)%的S是P」便可能同真,不是互斥的
命題。
由此可見,運用「第一形式」的關鍵在於尋找合適的「三分關係」,由於現實世界中很多事物往往具備多於三
種可能性,我們可按需要把某些可能性歸併;反之,我們亦可把某些本來渾然一體的事物人為地切分為三份;
此外我們還可以按需要對處於「三分關係」的三個命題與p、q、r的對應關係作出各種調配,這樣就為發掘新的
「對當方陣」提供廣闊的可能性。2.2小節以及本小節介紹的三種「相對數值對當方陣」其實就是對「多少n%的
S是P」的各種可能性作出不同切分和調配的結果。由此我們亦可斷言,「對當關係推理」絕非僅只「古典對當
方陣」所描述的一種,而是有無限種。
到目前為止,筆者還沒有討論過「例外結構」的「對當關係推理」。不過,在自然語言中,我們發現存在以下 推理關係:
上述推理的有趣之處在於,若把這兩句譯成英語,那麼前句的「除...外」應譯成"besides",而後句卻應譯成 "except"。由此我們想,能否構造一個包含"besides"和"except"的「對當方陣」?但若細心一想,我們會發現 情況頗為複雜,這是因為根據John是否具有某性質(即上例中的「穿T恤」)以及John以外的其他人是否具有該性 質,我們將得到一個「四分關係」而非「三分關係」,構不成「對當方陣」。為此,我們必須把情況簡化。一 種可行辦法是把「John具有某性質P」(以下簡稱「John是P」)作為「古典對當方陣」中四個語句的「附加預設」 (這裡還須假設John屬於主語集合S)。請注意這裡的「John是P」是作為「預設」而非「斷言」出現的,這樣做 是為了保證當我們否定某一「例外結構」時,作為「預設」的「John是P」不會被否定,例如儘管(1)中的兩句 互相矛盾,「John穿T恤」此一事實在這兩句中都保持不變。基於以上討論,我們可以構造以下的「例外 結構對當方陣」:
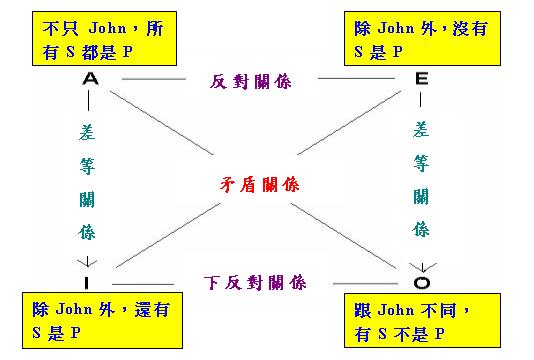
請注意在上述方陣中,A和O句分別使用介詞短語「不只John」(相當於英語的"not only John")和「跟John不同 」(相當於英語的"unlike John"),這是為了使「John是P」作為這兩句的「預設」。另請注意,由於「John是P 」具有「預設」而非「斷言」的性質,上述方陣中E句的集合論表達式不應為S ∩ P = {j},而應為
方陣中其他語句的集合論表達式也應含有「S − {j}」這個項。利用上述方陣,我們便可以把推理關係
(1)解釋成方陣中I與E句的「矛盾關係」。
由於「例外結構」可以採取多種形式,以上「對當方陣」其實還可以有其他變體,例如把方陣的「預設」改為
「John不是P」(各個語句也要作適當變更),或把"John"改為「S中一個成員」等等。
「對當方陣一般模式」也能應用於「模糊量詞」,不過這裡要用到模糊數學的一些成果。設有模糊量化句 Q(S)(P)和Q'(S')(P'),由於模糊量化句的真值是在區間[0, 1]中取值,而且其真值取決於某個「參項」值隸屬 「模糊量詞」的程度,我們可以把以上兩個模糊量化句的真值分別定為μ[Q](x)和μ[Q'](x'),其中x和x' 代表「參項」(這個「參項」一般等於集合的基數或集合基數之間的比率),例如模糊量化句「(almost all)(S)(P)」的真值便等於
接著我們定義模糊量化句之間的蘊涵關係。為避免討論毫不相干的模糊量化句之間的蘊涵關係(這裡所謂「毫不 相干」是指兩個模糊量化句沒有任何相同的成分),以下只討論那些具有至少一個相同成分(但非完全相同)的模 糊量化句的蘊涵關係(註3)。由於模糊量化句的真值取決於其「模糊量詞」和「參項」,以下我們將定義兩種蘊 涵關係。第一種蘊涵關係存在於具有相同「模糊量詞」(但「參項」不同)的語句之間,我們可以利用「隸屬度 函數」把這種蘊涵關係定義為:
第二種蘊涵關係則存在於具有相同「參項」(但「模糊量詞」不同)的語句之間,我們可以把這種蘊涵關係定義 為:
在以下的討論中,筆者將集中討論上述第二種蘊涵關係。
接著我們定義「模糊量詞」之間的包含關係。設有「模糊量詞」Q和Q',由於「模糊量詞」的「隸屬度函數」就
是把某個「參項」x的值映射到區間[0, 1]上的函數,我們可以定義Q和Q'之間的包含關係:
請注意上述定義其實只是模糊數學中模糊集合之間「包含」關係的推廣。形象地說,Q ⊆ Q'當且僅當 μ[Q](x)的圖象總是位於μ[Q'](x)的圖象之下。舉例說,如果我們把量詞"(a very large proportion of)" (相當於漢語的「非常多」)和"(at least a small proportion of)" (相當於漢語的「至少 一小部分」)的「隸屬度函數」分別定為(註4):
| 0, | if 0 ≤ x ≤ 0.8 | |
| μ[(a very large proportion of)](x) = | (x − 0.8) / 0.1, | if 0.8 ≤ x ≤ 0.9 |
| 1, | if 0.9 ≤ x ≤ 1 |
| 0, | if 0 ≤ x ≤ 0.2 | |
| μ[(at least a small proportion of)](x) = | (x − 0.2) / 0.1, | if 0.2 ≤ x ≤ 0.3 |
| 1, | if 0.3 ≤ x ≤ 1 |
以上兩個函數的圖象如下(註5):

從上圖可以看到,μ[(a very large proportion of)](x)的圖象(以紅色線表示)總是位於 μ[(at least a small proportion of)](x)的圖象(以藍色線表示)之下,由此可知
利用上述定義,容易推出以下有關「模糊量化句」之間蘊涵關係的定理:
定理1:設Q和Q'為「<1,1>型模糊量詞」並且Q ⊆ Q',則對任何集合S和P而言,均有以下「單向
蘊涵關係」:
現在,根據(4)和上述定理,可以推出
由於上式代表「單向蘊涵關係」,我們可以把它套用於「第二形式」,從而構造出以下的「模糊對當方陣」 :
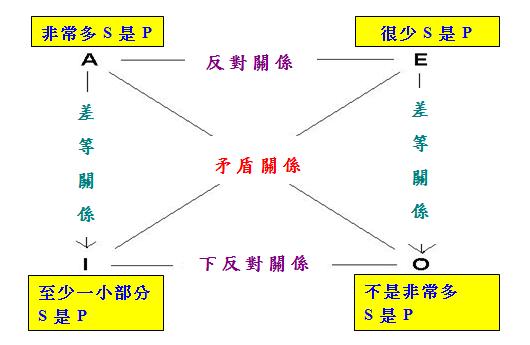
請注意在上述方陣中,筆者把「很少」當作「至少一小部分」的矛盾概念處理。說到這裡,有必要交代一下我 們應如何定義「模糊量詞」的矛盾概念。對於任一量詞Q而言,其否定~Q就是與Q矛盾的概念。根據模糊數學, 給定「模糊量詞」Q,一般可以根據Q的「隸屬度函數」把~Q的「隸屬度函數」定為:
舉例說,如果我們沿用上面"(a very large proportion of)"的「隸屬度函數」,那麼我們有
| 1, | if 0 ≤ x ≤ 0.8 | |
| μ[~(a very large proportion of)](x) = | (0.9 − x) / 0.1, | if 0.8 ≤ x ≤ 0.9 |
| 0, | if 0.9 ≤ x ≤ 1 |
上述定義亦顯示,「模糊量詞」Q和Q'存在「矛盾關係」當且僅當
請注意從某一角度看,上式類似命題邏輯中的下述定理:若命題p和p'是矛盾命題,則p ∨ p' = 1 (其中1代
表「真」)。
類似地,我們還可以定義「模糊量詞」之間的「(下)反對關係」如下:「模糊量詞」Q和Q'存在「反對關係」當
且僅當
Q和Q'存在「下反對關係」當且僅當
請注意以上兩個定義可被看成「反對關係」的「不可同真,但可同假」性質以及「下反對關係」的「不可同假 ,但可同真」性質在模糊集合上的推廣。
利用「第二形式」,我們也容易發掘包含「迭代量詞」的「對當方陣」,以下僅舉一例以作說明。根據「謂詞 邏輯」有關「邏輯依存」的理論,我們有以下「單向蘊涵關係」:
如果我們把上式中的S、T和P分別解釋為集合「男孩」、「女孩」和二元關係「愛」,便可得到上式的一個實例 :
現在,把上例套用於「第二形式」,並且運用「謂詞邏輯」中的兩個定理:
便可得到以下的「迭代量詞對當方陣」:
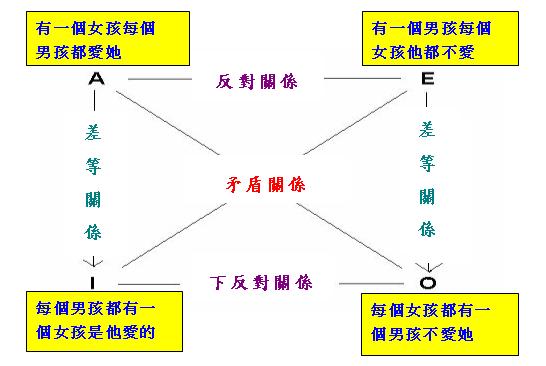
當然我們還可以構造更複雜或包含其他「迭代量詞」的「對當方陣」,這裡不擬作詳細討論。
筆者認為,我們還可以嘗試把「對當關係推理」推廣至「疑問量詞」,但由於疑問句跟命題不同,本身沒有真
假可言,我們須先為疑問句之間的推理關係提供一個定義。有關疑問句的推理關係,是當前「問題邏輯」和「
疑問語義學」的研究課題。筆者在《廣義量詞系列:特殊單式量詞》中曾指
出,當前的「疑問語義學」大致上可分為兩派:「選項語義學」和「結構化意義語義學」。這兩派的區別在於
,他們把疑問句的「解答」看成類型不同的語言/邏輯實體。筆者在以往一直採用「結構化意義語義學」的觀
點,把「解答」處理成謂詞或個體。不過Groenendijk和Stokhof在Type-Shifting Rules and the
Semantics of Interrogatives一文中指出此一觀點不適合用來表達疑問句之間的推理關係,他們主張採用
「選項語義學」的觀點,把「解答」處理成命題,這樣便可以把疑問句之間的推理關係最終歸結為命題之間的
關係。
Groenendijk和Stokhof還指出,儘管上述兩派在觀點上各有不同,但並非不可調和。由於兩派各有其優點,他
們主張採取兼容的態度,即認為兩派對「解答」的看法都是對的,各適用於不同的場合。但這麼一來,同一個
疑問句在不同情況下便會被解釋成不同類型的實體。為了解決這個問題,他們利用「類型轉換」
(Type-Shifting)的概念,指出一個疑問句的語義類型可透過「類型轉換」變為另一種語義類型。其實,筆者在
《廣義量詞系列:從量詞到廣義量詞》已曾介紹過「類型轉換」的概念,指
出此一概念可用來解釋以下現象:專有名詞的語義類型在某些情況下是e,在其他一些情況下則是(e → t)
→ t。Groenendijk和Stokhof的工作只是把「類型轉換」的應用領域從專有名詞擴大至疑問句而已。
以下筆者將採納Groenendijk和Stokhof的觀點,在討論疑問句的推理關係時,把「解答」處理成命題。此外,
正如筆者在《廣義量詞系列:模態量化結構》中所曾指出的,我們可以把一
個命題理解成使該命題為真的「可能世界」組成的集合,這樣,「解答」便等同於「可能世界集合」。為方便
以下討論,我們在這裡引入一些符號。在日常語言中,對某問題q的解答通常都以詞或短語的形式出現,當然我
們總可以把這些「非命題形式的解答」轉換成「命題形式的解答」。為區分這兩種解答,我們把前者記作a,把
後者記作q(a)。舉例說,設q為問題「多少個學生穿校服?」,a為解答「三個」,那麼q(a)就是命題「三個學
生穿校服」。此外,我們把使命題q(a)為真的「可能世界集合」記作World(q(a))。
以下筆者將使用上述概念定義疑問句之間的「蘊涵關係」:疑問句q蘊涵疑問句q',當且僅當對每個可能解答a
而言,World(q(a))都是World(q'(a))的子集(註6)。進一步我們還可以定義疑問句之間的「差等關係」(即「單
向蘊涵關係」),只需把以上定義中的「子集」改為「真子集」便行了。用集合論語言來表達,這就是:
接著我們根據上述定義考察以下兩個疑問句之間的「差等關係」:
為簡化討論,以下假設S有可數無限個元素,並以wn (n = 0, 1, 2, ...)代表共有n個S是P的「可 能世界」。由於在日常語言中,我們一般不會說「?超過0個S是P」,上述疑問句q1的可能解答包括 :1、2、3 ...。對應於每個可能解答n是一個「可能世界集合」World(q1(n)),例如 World(q1(1))就是{w2, w3, w4, ...}。以下列出每個 World(q1(n))的元素:
| World(q1(1)) = {w2, w3, w4, ...} | (7) |
| World(q1(2)) = {w3, w4, w5, ...} | |
| World(q1(3)) = {w4, w5, w6, ...} | |
| ... |
同理,我們亦可求得對應著q2的每個可能解答n的「可能世界集合」World(q2(n)):
| World(q2(1)) = {w1, w2, w3, ...} | (8) |
| World(q2(2)) = {w2, w3, w4, ...} | |
| World(q2(3)) = {w3, w4, w5, ...} | |
| ... |
容易看到上面的(7)和(8)符合(6)的條件,所以q1和q2存在「差等關係」。
類似地,我們亦可以定義疑問句之間的其他「對當關係」。「矛盾關係」表達一種「不可同真且不可同假」的
關係,即q與q'的解答互斥且窮盡一切可能性,此一關係反映在「可能世界集合」上便相當於(在下式中,W代表
所有「可能世界」組成的論域):
接著我們考察以下疑問句與上面q1的「矛盾關係」:
基於前面的假設,我們可以求得對應著q3的每個可能解答n的「可能世界集合」 World(q3(n)):
| World(q3(1)) = {w0, w1} | (10) |
| World(q3(2)) = {w0, w1, w2} | |
| World(q3(3)) = {w0, w1, w2, w3} | |
| ... |
容易看到上面的(7)和(10)符合(9)的條件,所以q1和q3存在「矛盾關係」(請注意W =
{w0, w1, w2, ...})。
接著考慮「反對關係」,這種關係就是「不可同真,但可同假」的關係,即q與q'的解答互斥但並不窮盡一切可
能性,此一關係反映在「可能世界集合」上便相當於:
最後考慮「下反對關係」,這種關係就是「不可同假,但可同真」的關係,即q與q'的解答窮盡一切可能性但不 互斥,此一關係反映在「可能世界集合」上相當於:
定義了疑問句之間的各種「對當關係」,我們便可以構造涉及「疑問量詞」的「對當方陣」。可是,由於自然 語言的「疑問詞」的語義非常單一,大部分「疑問詞」其實都只是「甚麼」的變體(例如「誰」等於「甚麼人」 、「何時」等於「甚麼時間」、「哪裡」等於「甚麼地點」等),如要發掘「疑問量詞」之間的「對當關係」, 只能從「複合疑問量詞」著手。一個可行的途徑是,把數量比較詞「超過」等與疑問詞「多少」結合起來,形 成「超過多少」、「不足多少」、「至少多少」和「最多多少」等「複合疑問量詞」,然後套用前文2.2小節的 「數值對當方陣(第一型)」,從而構造以下的「疑問對當方陣」(須假設S有可數無限個元素):
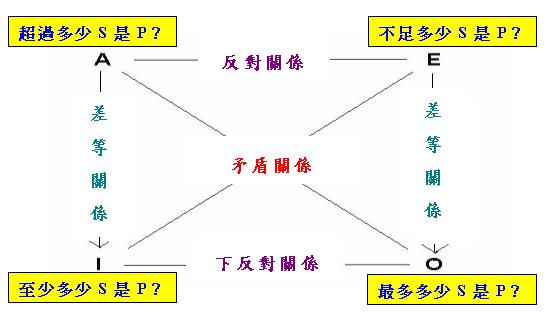
上述方陣的某些關係(包括A與I句的「差等關係」以及A與O句的「矛盾關係」)在前面已得到驗證,其他關係也
不難驗證,例如容易驗證上面的(8)與(10)符合(12)的條件,從而驗證I與O句的「下反對關係」。
以上是筆者發掘「疑問量詞」的「對當關係推理」的初步嘗試,有關這方面的研究還有待展開,討論只能到此
為止。
正如我們可以把「古典對當方陣」應用於其他論域一樣,我們也可以把本文介紹的包含各種「廣義量詞」的「 對當方陣」應用於其他論域。由於筆者在《廣義量詞系列:古典推理模式》 中已討論了各種論域上的「對當關係推理」,這裡無意逐一考慮這些論域,只擬就幾個較特別的實例作出 討論。
筆者在《廣義量詞系列:相關詞與度量結構》中介紹了「模糊限制語」的 概念,並指出各個「模糊限制語」有相關的「隸屬度函數」,例如在該網頁中,與「模糊限制語」VERY相關的 「隸屬度函數」便與上面2.3.5小節「模糊量詞」"(a very large proportion of)"的「隸屬度函數」 具有相同的形式。事實上,正如「相對數量詞」"all"、"no"等分別與「比例修飾語」 COMPLETELY、NOT-AT-ALL等存在對應關係一樣,某些表達相對數量的「模糊量詞」也與「模糊限制語」存在某 種對應關係(儘管這種對應關係不是絕對的),例如不妨把"(a very large proportion of)"與VERY、 "(a small proportion of)"與A-BIT對應起來等等。透過這種對應關係,我們便可以把上面2.3.5小節 中的「模糊對當方陣」改造為以下包含「模糊限制語」的「對當方陣」:

筆者亦在《廣義量詞系列:模態量化結構》中介紹了「模糊模態」的概念, 我們可以把「模糊模態詞」看成「模糊限制語」與「模態詞」的結合,即把該網頁中的 VERY-LIKELY(e(X'))分析成VERY(LIKELY(e(X')))。這樣便可以構造包含「模糊模態詞」的「對 當方陣」,只需把上述方陣中的謂語P改為適當的「模態詞」(例如LIKELY(e(X'))、 PLAUSIBLE(e(X'))、ADVISABLE(e(X'))等)便行了。這樣,我們便可以發掘出某些涉及「模糊限 制語」或「模糊模態」的「對當關係推理」,例如:
筆者在《廣義量詞系列:相關詞與度量結構》中指出了「序數詞」與「例 外量詞」存在對應關係,簡單地說,「序數詞」"nth"對應著「例外量詞」"(all except n − 1)" (此外還有"first"對應著"all"和"last"對應著"no")。由於筆者在2.3.4小節介紹了「 例外結構對當方陣」,一個自然的推論是把這個方陣應用於「序數詞」,從而發掘有關「序數詞」的「對當關 係推理」。為此,我們須把上述方陣中的"John"改為「S中n個成員」(其實為了保證方陣中的「(下)反對關係」 成立,這裡還須假設S含有至少n + 1個元素),並把P解釋成某個「比較短語」,例如「站在較Bill前的位置」 (為避免自己跟自己比較,「比較短語」中的個體不應屬於S)。當然我們還要修改上述方陣中各個語句的文字, 以符合通常的語言習慣。為具體說明上述方法,以下討論一個排隊的情況。設論域U為人的集合,b代表Bill, S代表與Bill站在同一條隊伍中的人組成的集合(請注意b ~∈ S),P代表「站在較Bill前位置的人」的集 合,並設n = 2,因此這裡預設至少有一人站在Bill之前,而且Bill所屬那條隊伍應有至少2 + 1 + 1 = 4人( 即|S ∪ {b}| ≥ 4)。把以上概念代入「例外結構對當方陣」,並對方陣上的文字略作修改後,便可得 到以下的「序數詞對當方陣」:
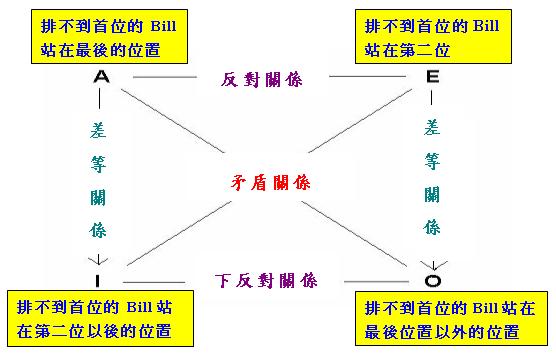
請注意上述方陣中四個語句的主語都含有短語「排不到首位的」,這是要突出這四句所包含的「預設」。此外 ,方陣中的E句應用了以下等價關係:
現在讓我們驗證上述方陣中的「反對關係」。由於隊伍包含至少4人,而且至少有一人站在Bill之前,方陣中的 A和E句顯然不可同真,但可同假,令這兩句同假的情況就是Bill站在第三至倒數第二位置之間的任何一個位置 (例如第三位),請注意此一情況亦可作為I和O句可同真的例證。
筆者在《廣義量詞系列:空間量化結構》中指出"inside"、"outside"和
"overlapping"分別與量詞"all" 、 "no" 和"some"存在對應關係,可是此一對應關係
只涵蓋了自然語言中表達空間關係的詞語的一小部分。不過,「對當方陣一般模式」為我們發掘涉及空間關係
的「對當關係推理」提供了廣闊的可能性,以下筆者用一個例子說明有關方法。
設我們在談論John對著一個高度基準向上跳的情況,那麼有且只有如下圖所示的三種可能結果:

在上圖中,橙色長方形代表John的身軀,藍色粗線代表高度基準,左、中和右圖分別代表John的整個身軀、部 分身軀和沒有一部分身軀在基準之上。由於這三種情況構成一個「三分關係」,我們可以利用「第一形式」構 造一個「對當方陣」。如果我們用p、q和r分別代表上面的左、中和右圖,那麼我們可以把p描述為「John能跳 過基準」("John can jump above the benchmark."),r描述為「John跳起來達不到基準」("John cannot reach the benchmark when he jumps up."),p ∨ q描述為「John跳起來能達到基準」("John can reach the benchmark when he jumps up."),以及r ∨ q描述為「John不能跳過基準」("John cannot jump above the benchmark.")。這樣,我們便得到以下這個「空間關係對當方陣」:

從這個「對當方陣」,我們可以得到某些推理結果,例如John跳起來可以既達到基準,又跳不過基準(此即上面 中圖的情況),但絕不可能既達不到基準,又跳過基準,等等。
經過以上的討論,相信讀者應已察覺,「對當方陣一般模式」只與「三分關係」或「單向蘊涵關係」有關,而 與量詞並無必然聯繫,因此「對當方陣一般模式」的應用可完全越出量詞的範圍,用來解釋某些涉及謂詞的推 理(註7)。以下舉一個涉及政治詞匯的例子。假設我們可以按政治取向把某地的政治人物分為「右」、「左」和 「中間」三派,而且上述劃分符合「三分關係」的要求。如果我們把這三派分別定為p、q 和r (註8),並把p ∨ q 稱為「兩極陣營」,r ∨ q 則稱為「中左陣營」(這裡「陣營」一詞只是類別標籤,不代表政治聯盟 ),那麼便可構造以下的「謂詞對當方陣」:

從這個「對當方陣」,我們可以得到以下推理結果:如果某人不屬於「中間派」,那麼他必定屬於「兩極陣營」
;某人既可屬於「兩極陣營」又屬於「中左陣營」(他是「左派」),但不可能兩者都不屬於,等等。以上例子
顯示,我們可以把「對當關係推理」從「量詞」之間的推理推廣為「謂詞」之間的推理,由此可見「對當方陣
一般模式」有著極其廣闊的應用空間。
至此筆者已討論了「對當方陣一般模式」的各種應用,除此以外,「對當關係推理」在當代還有其他革新方向
,例如有些學者便把傳統的「對當關係推理」推廣為「對偶性推理」。由於「對偶性推理」包含豐富的內容,
本身自成一個體系,這將留待以後再詳細介紹。
筆者在《廣義量詞系列:古典推理模式》中介紹了三種「結構變換推理」 ,現在我們以新的角度重新觀察這些變換,並把這些變換推廣到其他量詞。「換質法」在實質上是一種「 雙重否定推理」,因此這種變換適用於任何量詞(包括「數量比較詞」、「模糊量詞」、「疑問量詞」等) ,並且變換前後的語句在邏輯上等價。具體例子如:
由於在自然語言中很多帶有否定詞的量化句在邏輯上等價於另一個不帶否定詞的量化句(例如「所有S都不是P」 等價於「沒有S是P」,「多於n%的S不是P」等價於「少於(100 − n)%的S是P」等),我們可以把經換質後 帶雙重否定的語句再變換成只含一重否定的等價句,從而掩蓋了「雙重否定推理」的表面形式。舉例說,上述 例子便可以進一步變換為:
「雙重否定推理」進一步還可以與「對偶性推理」聯繫起來,這將留待以後再詳細討論。
筆者在上述網頁還介紹了「換位法」,如果撇除可能出現雙層括號的複雜情況,這種變換的實質就是把「<1,1> 型量詞」Q(S)(P)變為Q(P)(S)。在「廣義量詞理論」中,若某「<1,1>型量詞」Q滿足以下關係,就稱Q是「 對稱」的(Symmetric):
因此在傳統推理中能自由「換位」的語句就是那些含有「對稱量詞」的語句。筆者在上述網頁中亦曾指出,在
古典形式邏輯中,E和I句(即形式為「no(S)(P)」和「some(S)(P)」的語句)可以自由「換位」
,現在我們可以用「對稱性」來解釋箇中原因。由於「no(S)(P)」和「some(S)(P)」的真值條
件分別為S ∩ P = Φ和S ∩ P ≠ Φ,基於「∩」運算的「交換性」,把以上兩式中的S和
P換位後等價於原式,所以上述兩個量詞都是「對稱量詞」,E和I句因此可自由「換位」。
明白了這個原理,我們便可以把古典形式邏輯的「換位法」推廣為「對稱性推理」:只要「<1,1>型
量詞」Q具有「對稱性」,便可以把Q(S)(P)自由變換為Q(P)(S)。「對稱性推理」的關鍵在於確定哪些量詞是「
對稱」的,而根據上段的討論,「對稱量詞」"no"和"some"的集合論定義都含有「∩」運算
符,所以「對稱量詞」的主要來源應是那些在其定義中含有「∩」運算符的「<1,1>型量詞」。根據各個量
詞的集合論定義,我們不難找出某些「絕對數量比較詞」(例如"(more than n)"、"(between m and
n)"、"(an even number of)"等)(註9)、「模糊量詞」(例如"(about n)"、"(much
more than n)"等)、「疑問量詞」(例如"which"、"(how many)"等)、「例外量詞」(例如
"(no except n)"、"(no except John)"等)都是對稱的,因此含有這些量詞的語句都可進行「
對稱性推理」,例如:
如果我們把「~」與其後的論元作為一個整體參加「換位」,那麼「對稱性推理」也適用於某些帶有否定成分的 語句,例如把Q(~S)(~P)變成Q(~P)(~S)。在這種新約定下,在古典形式邏輯中不能自由「換位」的O句也可進行 「對稱性推理」,例如:
由於「對稱性」是一個廣泛存在的概念,例如在數學和物理學上「對稱性」便是十分重要的概念,所以「對稱
性推理」應不只局限於上面提到的情況,而應可推廣到更廣闊的層面。本文無意對「對稱性」作全面考察,這
裡只簡單討論一下涉及某些數量比較和空間關係概念的「對稱性推理」,因為這些概念可以像量詞那樣表達為
「三分結構式」。
筆者在《廣義量詞系列:時間量化結構》中曾指出,我們可以把含有「數量
比較詞」的算式表達為「三分結構式」,例如x = y和x ≈ y便可以分別表達為
其實表達空間關係的介詞也可作相同處理,例如"A is near B."和"A is far away from B."便可以分別表達為 (註11):
把表達數量比較和空間關係的語句也寫成「三分結構」後,我們便可以把這些語句的「對稱性推理」也表達為
的形式,惟請注意上式中的「Q」已不一定是量詞,而是泛指一般「算子」。根據各種「數量比較詞」和介詞的 語義,容易看到「=」、「≠」、「≈」(註12)、"outside"、"overlapping"、 "near"、"(close to)" 、 "opposite" 、 "beside"、"(next to)"以 及「相交修飾語 + "away from"」(例如"(far away from)"、"(10 m away from)")等都具有「 對稱性」,因而都可用於「對稱性推理」,例如:
在幾個最常用的量詞中,"all"是不對稱的,以下無效推理可佐證這一點:
不過,如果我們把上面右式中的量詞"all"改為"only",則可得到以下有效推理:
這是因為"all"與"only"互為「逆向反義詞」(Reversal Antonym)(又稱「關係反義詞」 Relational Antonym)。因此如果我們把眼光放遠一點,提出「逆向反義量詞」的概念,便可發掘出一種新型的 推理關係-「逆向性推理」。具體地說,若一對「<1,1>型量詞」Q和Q'滿足以下關係,就稱Q與Q'互 為「逆向反義詞」:
請注意如果把上式中的Q'改為Q,我們便得到「對稱量詞」的定義。由此可見,「對稱量詞」可被看成某種以自
身作為「逆向反義詞」的量詞。換句話說,「逆向性推理」可被視為「對稱性推理」的推廣。
不過,縱觀筆者以往介紹的量詞,除了那些同時具有「對稱性」的量詞外,便只有"all"與
"only"這一對「逆向反義詞」,因此「逆向性推理」在「廣義量詞理論」中似乎是一種沒有很大重要性
的推理模式。不過如果我們以廣闊的目光,把表達數量比較和空間關係的詞項也考慮進來,便會發現「逆向性
推理」並非罕見的推理模式。下表列出一些互為「逆向反義詞」的常用「數量比較詞」和介詞:
根據上表,我們可以作出一系列「逆向性推理」,例如:
正如我們可以把「對當關係推理」推廣至一般謂詞,「逆向性推理」也可以作類似推廣。事實上,在自然語言 中,「逆向反義詞」是一種常見的現象,並體現為多種詞類,包括名詞、動詞、形容詞等,以下是「逆向性推 理」的一些實例:
其實「逆向反義詞」本來就是語義學的一個重要課題,以往形式語義學一般採用「意義公設」的方法處理「逆 向反義詞」,即在語義模型中規定某些詞為「逆向反義詞」,這種方法帶有「特設」(ad hoc)的性質。筆者認 為我們應可把「逆向性」上升為一種存在於量詞、數量比較詞以及空間介詞之中的普遍性質,使之與「對稱性」 等性質並列,這樣我們便可以統一解釋存在於上述詞項之間的類似推理現象。
筆者在《廣義量詞系列:古典推理模式》中還介紹了「換質位法」,這種 變換包含多種形式。由於這些形式在現代觀點下,大多可歸結為「雙重否定推理」或「對稱性推理」(參見註10 ),這裡只擬討論其中一種較特殊的形式,用「三分結構」表達,這種形式就是把Q(S)(P)變換為Q(~P)(~S)。以 下筆者借用Zuber在More Algebras for Determiners一文中的「逆反性」概念,把上述這種變換推廣為 「逆否性推理」。具體地說,若某「<1,1>型量詞」Q滿足以下關係,就稱Q是「逆否」(亦 譯作「逆反」)的(Contrapositional):
請注意「逆否性」其實反映了「命題邏輯」中「充分條件句」的「假言易位律」,而在古典形式邏輯中只有A句
能進行這種推理,這是因為A句的量詞"all"正好對應著「充分條件句」。現在我們看能否發掘更多可進
行「逆否性推理」的量詞?
首先,筆者在《廣義量詞系列:基本單式量詞》中曾指出,「全稱量詞」
"all"在自然語言的語義中具有普遍性,「有定限定詞」和多種「光桿名詞短語」(包括「專有名詞」、
光桿「類名詞」和光桿「抽象名詞」)都可被分析成表達「⊆」關係的量詞,因此含有這些詞項的語句似乎
都可以進行「逆否性推理」。不過由於「有定限定詞」包含「預設」,在進行上述變換時,這個「預設」會被
改變,所以「有定限定詞」不能進行上述推理。至於上述各種「光桿名詞短語」,理論上它們應可進行「逆否
性推理」,例如下列等價關係便都是有效的(請注意在下例中,處於「⇔」右端的語句都加了適當的詞以使
這些語句更合語法):
其次,某些「例外量詞」可被看成是從"all"派生出來的量詞,包括"(all except n)"、 "(all except John)"等,這些量詞也可用於「逆否性推理」,例如:
最後,根據「命題邏輯」,除了「充分條件句」外,「必要條件句」也滿足「假言易位律」。由此可以推斷, 對應著「必要條件句」的量詞"only"也可用於「逆否性推理」,例如:
上述Zuber的文章以及Keenan的Excursions in Natural Logic一文中還提到量詞的另一種性質-「不動 點」(Fixed Point)(或者更確切地說,「謂語否定不動點」Fixed Point with respect to Predicate Negation)(註13)。具體地說,若某「<1,1>型量詞」Q滿足以下關係,就稱Q是「謂語否定不動點」) :
Zuber和Keenan各自在其文章中列舉了一些「謂語否定不動點」的例子,其中較常見的包括:"(exactly half)"、"(some but not all)"、"(between 1/3 and 2/3)"、"(less than 1/3 or more than 2/3)"、"(all or no)"等,這些量詞可用於以下的「不動點推理」:
讀者可自行驗證上述推理的有效性。由於上述推理已涉及到「對偶性」的問題,這裡只作簡略介紹,較詳細的
內容將留待以後再介紹。
根據對稱性,我們還可以定義其他「不動點」,例如以下兩式便可分別作為「主語否定不動點」
(Fixed Point with respect to Subject Negation)和「主謂否定不動點」(Fixed Point with
respect to Subject-Predicate Negation)的定義:
可是,這些「不動點」究竟是否存在於自然語言中?根據上段,「謂語否定不動點」大多表現為複合型量詞, 由此可以推斷,「主語否定不動點」和「主謂否定不動點」也應從複合型量詞中去找。根據筆者的初步考察, 這兩類「不動點」非常罕見,筆者所能想到的只有以下兩個似乎有點「人工化」的量詞,分別作為「主語否定 不動點」和「主謂否定不動點」:"(some but not restricted to)"和"(all and only)",相 關的推理實例如下:
不過,上述例句中的量詞不太自然,由此可見,上述兩類「不動點」似乎已超出了自然語言量詞的範疇,有關
問題尚有待研究。
至此筆者已討論了多種「結構變換推理」。現在讓我們來看看上述變換與邏輯學和數學上經常討論的三種變換
的關係。這三種變換都是對「充分條件句」的變換,分別稱為「逆命題」(Converse)、「否命題」(Inverse)和
「逆否命題」(Contrapositive)。用「命題邏輯」的符號來表達,這三種變換分別把s ⇒ p變成p ⇒
s、~s ⇒ ~p和~p ⇒ ~s。如果我們把這三種變換推廣為量化句的變換,那麼這三種變換便分別對應於
把Q(S)(P)變成Q(P)(S)、Q(~S)(~P)和Q(~P)(~S)。現在我們看到,上述第一種變換(即「逆命題」)對應於3.2小
節討論的「對稱性推理」,第三種變換(即「逆否命題」)對應於3.4小節討論的「逆否性推理」,而第二種變換
(即「否命題」)則對應於本小節討論的「主謂否定不動點推理」。至此我們再一次看到,只要從較高的視點觀
察,我們將看到不同學科、不同分支的某些推理其實互有關連。


