廣義量詞系列：量詞的邏輯性質

1. 引言

廣義量詞理論與現代數理邏輯有密切的關係，「量詞」本來就是來自謂詞邏輯的概念，因此我們可以把廣義量詞理論看成謂詞邏輯的一種推廣。不過，廣義量詞理論的研究對象包含「非經典」的量詞，而且由於它是作為一種自然語言的語義理論而非純邏輯理論，它不能不顧及自然語言的某些特點，因此其內容必然跟謂詞邏輯存在一定差異。

在本章，筆者將介紹廣義量詞理論中與謂詞邏輯相關的某些課題，本章的內容將圍繞兩大性質：「可歸約性」(Reducibility)和「可定義性」(Definability)。「可歸約性」其實是兩種性質－「類可歸約性」和「存在性」的統稱，這兩種性質主要跟「<1,1>型量詞」(即「限定詞」)有關。「可定義性」的種類則更加繁多，本文將主要介紹「一階可定義性」、「一階(量詞)可定義性」以及與單調量詞相關的可定義性。

鑑於上述課題的某些方面涉及艱深的現代邏輯概念及理論，對於部分定理，本章只提供其內容及例證而略去有關證明。此外，由於筆者所知有限，本章未能涵蓋此一課題的所有方面，特別是廣義量詞理論與「公理化」、「證明論」、「模態邏輯」、「條件句邏輯」等的關係。

2. 類可歸約性

2.1 基本概念

自然語言量化句跟傳統謂詞邏輯量化表達式的最大差別是，前者在句法上區分為主語和謂詞兩部分，其中主語的部分又可進一步區分為限定詞和普通名詞這兩部分，在語義上可表達為一個「三分結構」Q(A)(B)，其中Q、A 和B分別對應著限定詞、普通名詞和謂語，而三分結構式正是廣義量詞理論表達自然語言量化句的方式；後者則表達為Qx(p(x))的形式，其中Q、x和p(x)分別為量詞、變項和命題函項。試比較以下例句的三分結構式與謂詞邏輯表達式：

表1
例句	廣義量詞理論的三分結構式	謂詞邏輯量化表達式
Some boy sang.	some(BOY)(SING)	∃x ∈ U (x ∈ BOY ∧ x ∈ SING)
Every boy sang.	every(BOY)(SING)	∀x ∈ U (x ∈ BOY ⇒ x ∈ SING)

從量化範圍的角度看，自然語言量化句是以主語中的普通名詞作為量化範圍，限定詞的作用就是說明這個範圍與謂語之間的邏輯關係，例如上面第一句便是以普通名詞"boy"所代表的集合BOY作為量化範圍，限定詞"some" 的作用就是說明BOY與謂詞"sing"所代表集合SING的交集非空，廣義量詞理論的三分結構式正好反映了這種結構關係。反之，謂詞邏輯量化表達式則是以整個論域U作為量化範圍。為了正確表達命題函項「x ∈ BOY」與「x ∈ SING」之間的關係，該表達式須使用命題聯結詞「∧」。用日常語言來表達，上述謂詞邏輯表達式的意思是，存在論域U中至少一個元素x，使得x既屬於BOY，又屬於SING。請注意根據數理邏輯與集合論的對應關係，我們亦可以把上述謂詞邏輯表達式改寫為以下謂詞邏輯三分結構式：

some(U)(BOY ∩ SING) (1)

當我們把例句中的限定詞從"every"改為"some"後，廣義量詞理論的三分結構式只作了輕微的相應改動，而謂詞邏輯表達式則除了要把量詞從「∃」改為「∀」外，還要把式中的命題聯結詞從「∧」改為「 ⇒」。根據命題邏輯中「蘊涵」的定義，我們亦可以把這個表達式改寫為

∀x ∈ U (x ~∈ BOY ∨ x ∈ SING)

根據數理邏輯與集合論的對應關係，我們還可以把上述表達式進一步改寫為以下謂詞邏輯三分結構式：

every(U)(~BOY ∪ SING) (2)

把表1中的三分結構式與(1)－(2)比較，可以看到廣義量詞理論與謂詞邏輯的表達式的實質區別是，前者以簡單的集合A和B作為其三分結構式的第一和第二論元，後者則以整個論域U作為其三分結構式的第一論元，並以A和B 的某個「布爾組合」(Boolean Combination)作為第二論元，這裡「布爾組合」是指使用集合的「并」、「交」、「補」運算把A和B組合起來。由於這種「布爾組合」並非原有量化句的一部分，而是根據量化句的邏輯意義推導出來的，可見謂詞邏輯在表達自然語言量化句方面不及廣義量詞理論那樣直觀簡單。

除了"every"和"some"外，自然語言還有其他限定詞。現在的問題是，如果我們把上述例句中的限定詞改為其他限定詞，是否總有相應的謂詞邏輯三分結構式？如有的話，這個表達式又包含哪一種「布爾組合」？為解答這個問題，以下引入「類可歸約性」(Sortal Reducibility)(以下記作SR)的概念。我們說限定詞Q是「類可歸約」的當且僅當存在A、B的某個「布爾組合」Bool(A, B)，使得

Q(A)(B) ⇔ Q(U)(Bool(A, B)) (3)

如果Q不是「類可歸約」的，它就是「類固定」(Inherently Sortal)(記作~SR)的。此外，我們亦把 (3)中從左邊表達式轉換為右邊表達式的操作稱為「類歸約」(Sortal Reduction)。

2.2 主要定理

Keenan在Quantification in English is Inherently Sortal一文中研究了「類可歸約性」的問題，提出了一條完全確定「類可歸約限定詞」的定理。為方便以下的證明，這裡首先引入另一條定理。

定理1：	(i) Q ∈ INT當且僅當對任何A、B，均有Q(A)(B) ⇔ Q(U)(A ∩ B)。
	(ii) Q ∈ RC-INT當且僅當對任何A、B，均有Q(A)(B) ⇔ Q(U)(~A ∪ B)。
	(iii) 如對任何A、B，均有Q(A)(B) ⇔ Q(U)(~A ∪ ~B)，則Q ∈ INT。
	(iv) 如對任何A、B，均有Q(A)(B) ⇔ Q(U)(A − B)，則Q ∈ RC-INT。

以下證明(i)。首先設Q ∈ INT，那麼由於A ∩ B = U ∩ (A ∩ B)，因此根據INT的定義，有 Q(A)(B) ⇔ Q(U)(A ∩ B)。其次設Q(A)(B) ⇔ Q(U)(A ∩ B)，並設A ∩ B = C ∩ D。那麼我們有Q(A)(B) ⇔ Q(U)(A ∩ B) ⇔ Q(U)(C ∩ D) ⇔ Q(C)(D)，由此證得Q ∈ INT。綜合以上結果，(i)乃得證。

接著證明(ii)。首先設Q ∈ RC-INT，那麼由於A − B = U − (~A ∪ B)，因此根據RC-INT 的定義，有Q(A)(B) ⇔ Q(U)(~A ∪ B)。其次設Q(A)(B) ⇔ Q(U)(~A ∪ B)，並設A − B = C − D。那麼我們有Q(A)(B) ⇔ Q(U)(~A ∪ B) ⇔ Q(U)(~(A − B)) ⇔ Q(U)(~(C − D)) ⇔ Q(U)(~C ∪ D) ⇔ Q(C)(D)，由此證得Q ∈ RC-INT。綜合以上結果，(ii)乃得證。

接著證明(iii)，設Q(A)(B) ⇔ Q(U)(~A ∪ ~B)，並設A ∩ B = C ∩ D，即~A ∪ ~B = ~C ∪ ~D。那麼我們有Q(A)(B) ⇔ Q(U)(~A ∪ ~B) ⇔ Q(U)(~C ∪ ~D) ⇔ Q(C)(D)，由此證得Q ∈ INT。

最後證明(iv)，設Q(A)(B) ⇔ Q(U)(A − B)，並設A − B = C − D。那麼我們有 Q(A)(B) ⇔ Q(U)(A − B) ⇔ Q(U)(C − D) ⇔ Q(C)(D)，由此證得Q ∈ RC-INT 。

定理2：在CONS_r下，SR = INT ∪ RC-INT。

以下證明上述定理，首先證明INT ∪ RC-INT ⊆ SR。設Q ∈ INT，那麼根據「定理1(i)」，我們有Q(A)(B) ⇔ Q(U)(A ∩ B)。其次設Q ∈ RC-INT，那麼根據「定理1(ii)」，我們有Q(A)(B) ⇔ Q(U)(~A ∪ B)。由於A ∩ B和~A ∪ B都是A、B的「布爾組合」，我們證得Q無論是屬於INT 還是RC-INT，都有Q ∈ SR，即INT ∪ RC-INT ⊆ SR。

其次證明SR ⊆ INT ∪ RC-INT。設Q ∈ SR，即Q滿足(3)。請注意A、B的「布爾組合」雖然可以千變萬化，但其最終結果卻是有限的。舉例說，根據集合論，我們知道~A ∪ ~B與~(A ∩ B)這兩個「布爾組合」是等價的。那麼共有多少種互不等價的Bool(A, B)？由於集合A和B把論域U分割成四個不相交的區域：A − B、B − A、A ∩ B和~A ∩ ~B，這四個區域的每種組合各對應著某種Bool(A, B)，例如前述的~A ∪ ~B便對應著由A − B、B − A和~A ∩ ~B加起來的部分。由於四個區域共有16 種可能組合，所以共有16種互不等價的Bool(A, B)，我們可以把它們全部列出如下：

Bool₁(A, B) = U	Bool₂(A, B) = Φ
Bool₃(A, B) = A	Bool₄(A, B) = ~A
Bool₅(A, B) = B	Bool₆(A, B) = ~B
Bool₇(A, B) = A ∩ B	Bool₈(A, B) = ~A ∪ ~B
Bool₉(A, B) = A − B	Bool₁₀(A, B) = ~A ∪ B
Bool₁₁(A, B) = B − A	Bool₁₂(A, B) = A ∪ ~B
Bool₁₃(A, B) = ~A ∩ ~B	Bool₁₄(A, B) = A ∪ B
Bool₁₅(A, B) = (A − B) ∪ (B − A)	Bool₁₆(A, B) = (A ∩ B) ∪ (~A ∩ ~B)

請注意上面右欄每一行的集合都是左欄同一行集合的補集，在證明時可以把它們一併考慮。以下我們把上面每一行上的「布爾組合」逐一代入(3)中的Bool。首先，把Bool₁代入(3)，得Q(A)(B) ⇔ Q(U)(Bool₁(A, B)) ⇔ Q(U)(U)。由於Q(U)(U)的真值是一個常數，這說明Q等同於「恆真限定詞」1或「恆假限定詞」0，而INT ∩ RC-INT = {1, 0}(註1)。同理，把Bool₂代入(3)，得 Q(A)(B) ⇔ Q(U)(Φ)，Q的真值同樣是常數，由此有Q ∈ INT ∩ RC-INT。

其次，把Bool₃代入(3)，得Q(A)(B) ⇔ Q(U)(Bool₃(A, B)) ⇔ Q(U)(A) ⇔ Q(U)(Bool₃(U, A)) ⇔ Q(U)(U)。同理，把Bool₄代入(3)，得Q(A)(B) ⇔ Q(U)(~A) ⇔ Q(U)(Φ)。由於在上述兩種情況下，Q的真值都是常數，因此Q ∈ INT ∩ RC-INT。

接著，把Bool₅代入(3)並利用Q(A)(B) ⇔ Q(A)(A ∩ B) (「右守恆性」)，得Q(A)(B) ⇔ Q(U)(Bool₅(A, A ∩ B)) ⇔ Q(U)(A ∩ B)。由此根據「定理1(i)」，得Q ∈ INT。同理，把Bool₆代入(3)，得Q(A)(B) ⇔ Q(U)(~(A ∩ B)) ⇔ Q(U)(~A ∪ ~B)。由此根據「定理1(iii)」，亦可得Q ∈ INT。

接著，把Bool₇代入(3)，得Q(A)(B) ⇔ Q(U)(Bool₇(A, B)) ⇔ Q(U)(A ∩ B)。由此根據「定理1(i)」，得Q ∈ INT。同理，把Bool₈代入(3)，得Q(A)(B) ⇔ Q(U)(~A ∪ ~B)。由此根據「定理1(iii)」，亦可得Q ∈ INT。

接著，把Bool₉代入(3)，得Q(A)(B) ⇔ Q(U)(Bool₉(A, B)) ⇔ Q(U)(A − B)。由此根據「定理1(iv)」，得Q ∈ RC-INT。同理，把Bool₁₀代入(3)，得Q(A)(B) ⇔ Q(U)(~A ∪ B)。由此根據「定理1(ii)」，亦可得Q ∈ RC-INT。

接著，把Bool₁₁代入(3)，得Q(A)(B) ⇔ Q(U)(Bool₁₁(A, B)) ⇔ Q(U)(B − A) ⇔ Q(U)(Bool₁₁(U, B − A)) ⇔ Q(U)(Φ)。同理，把 Bool₁₂代入(3)，得Q(A)(B) ⇔ Q(U)(A ∪ ~B) ⇔ Q(U)(U)。由於在上述兩種情況下，Q的真值都是常數，因此Q ∈ INT ∩ RC-INT。

接著，把Bool₁₃代入(3)，得Q(A)(B) ⇔ Q(U)(Bool₁₃(A, B)) ⇔ Q(U)(~A ∩ ~B) ⇔ Q(U)(Bool₁₃(U, ~A ∩ ~B)) ⇔ Q(U)(Φ)。同理，把 Bool₁₄代入(3)，得Q(A)(B) ⇔ Q(U)(A ∪ B) ⇔ Q(U)(U)。由於在上述兩種情況下， Q的真值都是常數，因此Q ∈ INT ∩ RC-INT。

最後，把Bool₁₅代入(3)並利用Q(A)(B) ⇔ Q(A)(A ∩ B)得Q(A)(B) ⇔ Q(U)(Bool₁₅(A, A ∩ B)) ⇔ Q(U)(A − B)。由此根據「定理1(iv)」，得Q ∈ RC-INT。同理，把Bool₁₆代入(3)，得Q(A)(B) ⇔ Q(U)((A ∩ B) ∪ ~A) ⇔ Q(U)(~A ∪ B)。由此根據「定理1(ii)」，亦可得Q ∈ RC-INT。至此我們已考慮各種可能情況，由此證得SR ⊆ INT ∪ RC-INT。綜合以上情況，「定理2」得證。

2.3 例證

「定理2」告訴我們，「相交限定詞」和「右補相交限定詞」是「類可歸約」的。如果我們把「定理1(i)和(ii) 」分別與(1)和(2)比較，我們將會看到，「相交限定詞」和「右補相交限定詞」在進行「類歸約」後所得的「布爾組合」分別與"some"和"every"進行「類歸約」後所得的「布爾組合」具有相同的形式(註 2)。我們可以根據此一關係得到一些有效推理，首先看「相交限定詞」的例子：

Some boy is singing. ⇔ Some individual is a boy who is singing.
No boy except John is singing. ⇔ No individual except John is a boy who is singing.
Infinitely many points are contained in the circle.
⇔ Infinitely many individuals are points contained in the circle.

接著看「右補相交限定詞」的例子：

Every boy is singing. ⇔ Every individual is such that if he is a boy then he is singing.
Every boy except John is singing. ⇔ Every individual except John is such that if he is a boy then he is singing.
All but finitely many points are contained in the circle.
⇔ All but finitely many individuals are such that if it is a point then it is contained in the circle.

請注意上述例子包含兩個涉及「無窮基數」的限定詞"(infinitely many)"和"(all but finitely many)"，容易證明這兩個限定詞分別屬於INT和RC-INT。

「定理2」也告訴我們，其他限定詞都是「類固定」的。在自然語言中，最重要的「類固定限定詞」包括那些包含「預設」的限定詞，例如"the"、"John's"、"both"、"neither"等以及某些「右比例限定詞」(記作PROPORT_r)，例如"most"、"(less than q)"、"(no except q)"以及「右補右比例限定詞」(記作RC-PROPORT_r)，例如"(all except q)"等 (其中q代表小於1的分數)。上述這些限定詞都不能進行「類歸約」，例如以下推導便是無效的：

Most boys are singing. ~⇔ Most individuals are boys who are singing.

在一個論域中，如果男孩只佔少數，那麼不管唱歌者佔男孩的比例是多少，上面右句總是假的，而左句則可真可假。請注意不論我們對上面右句中"most individuals"後面的部分作何種修改，都無法使上述推導變得有效，其他「類固定限定詞」也是如此。由於「類固定限定詞」佔了自然語言限定詞的一大部分，自然語言限定詞在本質上不是「類可歸約」的，這說明了謂詞邏輯在表達自然語言量化句方面存在缺陷。

3. 存在性

3.1 存在句

筆者在《廣義量詞系列：時間量化結構》中介紹了英語的「存在句」，這種句子具有「There + be + Q + A (+ B)」的格式，其中Q和A分別為限定詞和普通名詞短語，B則是指放在A後的形容詞／介詞短語／分句等，稱為「後續成分」(Coda)，這個成分不一定要出現。上述網頁亦指出，「存在句」可被處理成一種「泛化量化結構」，表達成Q(A ∩ B)(U)的三分結構形式。例如語句

There are some students playing in the park.

的三分結構式便是

some(STUDENT ∩ {x: x is playing in the park})(U)

在英語中，並非任何限定詞都可出現於「存在句」中，請看以下例句：

There is no boy except John who knows the secret.
There were at least seven attendants in the meeting.
?There is every family member to support you.
?There are most students playing.

上面第一、二個例句是完全合語法的「存在句」，第三、四個例句如作為「存在句」看待是不合語法的，但如把"there"理解成其他意思，例如表示某種肯定語氣，或者表示「在那裡」，則或可接受。現在我們的問題是，如何確定哪些限定詞可以出現於「存在句」中。

3.2 主要定理

Keenan在A Semantic Definition of "Indefinite NP"一文中研究了「存在句」的限定詞問題，他提出 「存在性」(Existentiality)的概念，即限定詞Q是「存在」(記作EXIST)的當且僅當對任何A、B均有

Q(A)(B) ⇔ Q(A ∩ B)(U) (4)

把上述定義跟(3)比較，可以看到「存在性」跟「類可歸約性」有相似之處，兩者都把原來的三分結構Q(A)(B) 的其中一個論元變成論域U，而另一個論元則變成A和B的某種「布爾組合」，因此之故，本文把「存在性」也看成「可歸約性」的一種。

Keenan認為形如「There + be + Q + A + B」的「存在句」在語義上應被解釋成等同於「Q(A)(B)」(註3)。當Q 滿足定義(4)的條件時，這類「存在句」在邏輯上等價於Q(A ∩ B)(U)。這裡U作為一個謂詞性論元，可以被解讀成論域中所有元素都滿足的謂語，例如"exist"。換句話說，根據上述定義，上一小節舉出的合語法「存在句」都滿足以下等價關係：

There is no boy except John who knows the secret.	⇔ No boy except John knows the secret.
	⇔ Except for John, no boy who knows the secret exists.

There were at least seven attendants in the meeting.	⇔ At least seven attendants were in the meeting.
	⇔ At least seven attendants who were in the meeting existed.

Keenan認為，即使是不合語法的「存在句」也應被解釋成等同於「Q(A)(B)」。它們跟合語法「存在句」的區別僅在於在邏輯上並不等價於一個以"exist"作為謂語的量化句，例如

?There is every family member to support you.	⇔ Every family member is to support you.
	~⇔ Every family member who is to support you exists.

?There are most students playing.	⇔ Most students are playing.
	~⇔ Most students who are playing exist.

接著看以下定理：

定理3：在CONS_r下，EXIST = INT。

由於「存在性」的定義(4)跟「定理1(i)」中的等值式非常相似，兩者的區別只在於A ∩ B和U所在的論元位置。現在只要把「定理1(i)」的證明中A ∩ B和U對調位置，便即變成以下結果的證明：Q ∈ INT當且僅當對任何A、B，均有Q(A)(B) ⇔ Q(A ∩ B)(U)。由此根據(4)，「定理3」得證。

基於「存在性」的定義，Keenan指出只有以下「存在限定詞」(即「相交限定詞」)才能出現於「存在句」中：「簡單存在限定詞」(例如"some"、"(a few)"等)、帶有各種修飾語的基數詞(註4)(例如 "(infinitely many)")、"(about n)"、"(at least n)"、"(between m and n)"、"(an even number of)"等)以及具有「存在性」的「例外限定詞」"(no ... except John)"等。

Keenan並指出，並非所有「存在限定詞」都可出現於「存在句」中。因此，「存在性」只是可出現於「存在句」的必要條件而非充分條件。舉例說，"(either all or else not all)"便具有「存在性」，因為這個限定詞涵蓋所有可能性，實際等同於"1"，而1 ∈ INT (參見註1)；但這個限定詞在結構上類似限定詞 "all"，而後者不能出現於「存在句」中。

3.3 概念推廣

我們還可以把定義(4)及上述結果推廣至其他類型的量詞。首先，對於「<1>型量詞」(本文把某些具有數學或邏輯學意義的「<1>型量詞」以及自然語言中的「<−,1>型量詞」統稱為「<1>型量詞」)，我們可以借助《廣義量詞系列：量詞的普遍性質與操作》中的公式(33)。設Q為「<1>型量詞」，那麼我們有

Q(A) ⇔ Q^rel(U)(A)

其中rel為上述網頁介紹的「關係化」操作，例如everybody^rel = every、 somebody^rel = some等。利用上式和(4)，我們可以得到「<1>型量詞」的「存在性」的定義，即Q是「存在」的當且僅當對任何A都有

Q(A) ⇔ Q^rel(A)(U) (5)

容易證明"somebody"、"(nobody except John)"等都具有「存在性」，而"everybody" 、"(everybody except John)"等都則不具有「存在性」，此一結果可用來解釋以下句子為何可被視為符合／不合語法的「存在句」：

There is nothing inside the box.
There is somebody living here.
?There is everything you need.
?There was everybody except Mary in the ball.

其次考慮「<1²,1>型結構化量詞」，設Q為「<1²,1>型結構化量詞」，我們說Q是「存在」的當且僅當對任何A、B、C都有

Q(A, B)(C) ⇔ Q(A ∩ C, B ∩ C)(U) (6)

容易證明"(more ... than ....)"、"(exactly as many ... as ....)"等量詞都具有「存在性」，此一結果可用來解釋以下句子為何是合語法的：

There are more boys than girls participating in the game.
There are exactly as many boys as girls participating in the game.

儘管Keenan的上述理論具有一定說服力，但該理論仍有爭議性，亦有學者指出他的理論不能解釋的現象，因此「存在句」雖然看似一種簡單的語言現象，但仍有待學者作進一步研究。

4. 一階可定義性

4.1 基本概念

「一階邏輯」(First Order Logic)(簡稱FO，這裡是指「帶等詞的一階謂詞邏輯」)是在現代數理邏輯中最受重視的邏輯系統，因為它較為簡單，而且具有許多良好的元邏輯性質。不過，由於「一階邏輯」的「邏輯常項」只包括邏輯聯結詞(~、∧、∨、⇒、⇔)、兩個量詞(∀、∃)和一個等詞(=)，它的表達力十分有限。廣義量詞理論中的一個重要課題就是研究自然語言中哪些量詞可以用「一階語句」(First Order Sentence)來表達，所謂「一階語句」，就是指使用上述「邏輯常項」以及其他常項、變項，依照「一階邏輯」的形成規則，經有窮步驟形成的不含自由變項的合式公式(詳細內容請參閱《廣義量詞系列：現代推理模式》)。

接著引入限定詞的「一階可定義性」(First Order Definability)(記作FO-D)概念，設Q為限定詞，A 、B為其論元。我們說Q是「一階可定義」的當且僅當存在一個僅包含謂詞A和B以及其他變項、「邏輯常項」的「一階語句」p使得對任何語義模型M而言，

p在M中真 ⇔ Q(A)(B)在M中真

如上述條件成立，我們便說限定詞Q由表達式p定義。其他類型量詞的「一階可定義性」也可作類似定義。

最常用的兩個限定詞"every"和"some"顯然是「一階可定義」的，因為它們可被看成"∀" 和"∃"經「關係化」得來的結果。此外，還有很多限定詞也是「一階可定義」的，例如"(at least 3)(A)(B)"和"(at most 2)(A)(B)"便可分別用以下表達式來定義：

∃x∃y∃z (x ≠ y ∧ y ≠ z ∧ z ≠ x ∧ A(x) ∧ A(y) ∧ A(z) ∧ B(x) ∧ B(y) ∧ B(z))
∀x∀y∀z ((A(x) ∧ A(y) ∧ A(z) ∧ B(x) ∧ B(y) ∧ B(z)) ⇒ (x = y ∨ y = z ∨ z = x))

容易把上式推廣為"(at least n)(A)(B)"和"(at most n)(A)(B)"的表達式，不過隨著n增加，表達式會變得越來越長。定冠詞"the"也是「一階可定義」的，沿用Russell的分析， "the(A)(B)"可被定義為(註5)：

∃x∀y (A(x) ∧ (A(y) ⇒ y = x) ∧ B(x))

請注意當論域的基數有限且確定時，我們可以窮舉的方式定義某些限定詞。舉例說，如果知道|U| = 2n (n為自然數)，那麼"(an even number of)"便等同於"(no or exactly 2 or exactly 4 or ... exactly 2n)"，而"no"和"(exactly n)"都是「一階可定義」的。不過，「一階語言」並不包含集合基數的資料(註6)，因此不能說"(an even number of)"是「一階可定義」的(這個限定詞實際上不是「一階可定義」的，以下將予以證明)。以下在討論其他限定詞的「一階可定義性」時，我們必須撇除集合基數這一因素。

4.2 與左單調性的關係

當代廣義量詞理論的一項成就就是確定「一階可定義限定詞」的特徵，首先我們有以下定理。

定理4：在LOG ∩ FIN − TRIV下，設限定詞Q ∈ ↓MON，則Q的真值條件可以表達為以下析取三分結構式的合取(註7)：

(at most n)(A)(B) ∨ (at most m)(A)(~B) (7)

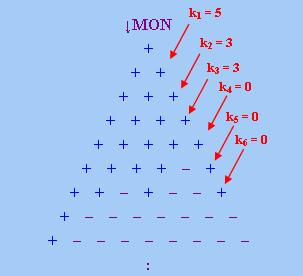
以下將借助「數字三角形」證明上述定理。為此，我們首先重溫「數字三角形」的結構：

以下我們把由[0, 0]、[1, 0]、[2, 0]...組成的一「列」稱為「第0列」，由[0, 1]、[1, 1]、[2, 1]...組成的一「列」稱為「第1列」，如此類推。我們也把由[0, 0]、[0, 1]、[0, 2]...組成的一「行」稱為「第0行」，由[1, 0]、[1, 1]、[1, 2]...組成的一「行」稱為「第1行」，如此類推。同理，我們也把由[0, 0]組成的「對角線」稱為「第0對角線」，由[1, 0]、[0, 1]組成的「對角線」稱為「第1對角線」，如此類推。

設Q ∈ ↓MON，根據《廣義量詞系列：單調性的進階研究》中的討論，Q的「數字三角形」具有以下特徵：假如某一位置有「+」號，那麼與該位置處於同一「行」或「列」並在其上方的所有其他位置都取「+」號。現在我們根據上述特徵看看每一「列」的情況。

對於每一「列」而言，有且僅有以下一種情況成立：(1) 全取「+」號；(2) 全取「−」號；(3) 既包含「+」號又包含「−」號。鑑於Q具有「左遞減性」，若某「列」全為「+」號，則其左上方各「列」也全為「+」號；若某「列」全為「−」號，則其右下方各「列」也全為「−」號；若某「列」(設為「第i列」)既有「+」號又有「−」號，那麼該「列」必有一個位置[k_i, i]，使得對所有j > k_i，[j, i]都取「−」號，並且對所有j ≤ k_i，[j, i]都取「+」號。請注意這個k_i會隨著i而變化，不過根據Q的「左遞減性」，我們必有若i > j，則k_i ≤ k_j。換句話說，「數字三角形」上每「列」的「+」號都集中於該「列」的上方，而各「列」所包含的「+」號數目沿右下方向順次遞減，如下圖所示(下圖最左一「列」全為「+」號)：

請注意上面的「數字三角形」(以下稱為「總圖」)可以被分解成以下四個互有重疊的「數字三角形」(以下稱為「分圖」)的「交集」：

上面四個「分圖」的共同點是，除了一個向下無限延伸的三角形外，所有其餘位置都取「+」號，這四個無限延伸的三角形的「并集」正好對應著「總圖」上取「−」號的位置。上面四個「分圖」可分別表達為：

no(A)(B) ∨ (at most 5)(A)(~B)
(at most 1)(A)(B) ∨ (at most 3)(A)(~B)
(at most 3)(A)(B) ∨ no(A)(~B)
(at most 6)(A)(B)

由於上面的「總圖」是上面四個「分圖」的「交集」，「總圖」所代表的限定詞可以表達為上述四個析取三分結構式的合取。

對於一般的「左遞減限定詞」而言，它們的「數字三角形」也可被分解成有限個類似上述「分圖」的「交集」。由於這些「分圖」都可被表達成(7)的形式，所以這些限定詞可被表達成形式為(7)的析取三分結構式的「合取」，「定理4」得證。

由於形式為(7)的析取三分結構式都是「一階可定義」的，根據「定理4」，我們容易得到以下結果：在LOG ∩ FIN − TRIV下，

↓MON ⊆ FO-D (8)

從(8)我們也容易推出以下結果：在LOG ∩ FIN − TRIV下，

↑MON ⊆ FO-D (9)

設Q ∈ ↑MON，那麼~Q ∈ ↓MON。根據(8)，得~Q ∈ FO-D，即~Q可定義為一個「一階語句」p。由此可知Q可定義為~p，而~p顯然也是一個「一階語句」，(9)乃得證。

4.3 與左連續性的關係

我們可以從「定理4」推導出以下定理。

定理5：在LOG ∩ FIN − TRIV下，CONT_l ⊆ FO-D。

設Q ∈ CONT_l，根據《廣義量詞系列：單調性的進階研究》中的討論，Q的「數字三角形」具有以下特徵：假如三角形上某兩個位置[x, y]和[x'', y'']取「+」號，而且該兩個位置滿足x ≤ x'' ∧ y ≤ y''，那麼以該兩個位置為端點，並以該兩個位置所在的「行」和「列」為邊的平行四邊形內所有其他位置都取「+」號。下圖顯示「左連續限定詞」的「數字三角形」特徵：

上圖還定義了四個數字：x₀為三角形中有「+」號的最右一「行」的x值；y₀為「第 x₀行」中有「+」號的最高位置的y值；y₁為三角形中有「+」號的最左一「列」的y值；x₁為「第y₁列」中有「+」號的最高位置的x值。

根據上述定義，有x₀ ≤ x₁，y₁ ≤ y₀。接著定義一個新的限定詞Q'如下：

Q'[x, y] ⇔ Q[x, y] ∨ (x₀ ≤ x ≤ x₁ ∧ y₁ ≤ y ≤ y₀)

上述定義的作用實際是使上圖中以[x₀, y₁]為頂端的某個有限範圍內全取「+」號。現在如果我們僅考慮Q'中{[x, y]: x ≥ x₀ ∧ y ≥ y₁]}的範圍，那麼Q'在這個範圍內具有「左遞減性」，而在該範圍外則全取「−」號。由此根據「定理4」，只要作出一些修正，便可把Q'表達為某些析取三分結構式的合取，即Q'是「一階可定義」的。由於Q'與Q只在{[x, y]: x₀ ≤ x ≤ x₁ ∧ y₁ ≤ y ≤ y₀}的有限範圍內存在差異，由此可知Q也是「一階可定義」的。

以上圖為例，我們把它代表的限定詞稱為Q。如果我們把Q中的[1, 1]和[2, 1]位置上的「−」號變為「+」號，便得到Q'。接著把Q'的「第0行」和「第0列」刪去，所得三角形(稱為Q'')等同於4.2小節的「總圖」。由此可知，Q''可以表達為4.2小節所列析取三分結構式的合取。接著我們要對這些析取三分結構式作適當修正，以便把Q''「還原」為Q' (即重新補上被刪去的「第0行」和「第0列」)，例如我們要把

no(A)(B) ∨ (at most 5)(A)(~B)

修正為

(exactly 1)(A)(B) ∨ (between 1 and 6)(A)(~B)

最後我們把Q'「還原」為Q (即把[1, 1]和[2, 1]位置還原為「−」號)，便可得到Q的表達式如下：

((exactly 1)(A)(B) ∨ (between 1 and 6)(A)(~B))
∧ ((between 1 and 2)(A)(B) ∨ (between 1 and 4)(A)(~B))
∧ ((between 1 and 4)(A)(B) ∨ (exactly 1)(A)(~B))
∧ (between 1 and 7)(A)(B)
∧ ~((exactly 1)(A)(~B) ∧ (exactly 1)(A)(B))
∧ ~((exactly 2)(A)(~B) ∧ (exactly 1)(A)(B))

由於以上各個合取項都是「一階可定義」的，所以Q也是「一階可定義」的。

我們還可以把「定理5」進一步推廣為以下定理。

定理6：設Q ∈ LOG ∩ FIN − TRIV，則Q ∈ FO-D當且僅當Q = Q₁ ∨ ... ∨ Q_k，其中Q₁ ... Q_k ∈ CONT_l。

設Q = Q₁ ∨ ... ∨ Q_k，其中Q₁ ... Q_k ∈ CONT_l，那麼根據「定理5」，Q₁ ... Q_k ∈ FO-D，由此可知Q ∈ FO-D。其次設Q ∈ FO-D，根據van Benthem在Questions About Quantifiers一文中的結果 (證明從略)，Q的「數字三角形」以「第2n對角線」(n為某非負整數)為分界線分為上下兩部分，該「對角線」及其以上部分的「+／−」號分佈可能無規律可言，但該「對角線」以下部分的「+／−」號分佈卻呈現局部規律性，具體表現為：(1) 若[n, n]位置取「+」(「−」)號，則以[n, n]為頂點的整個三角形都取「+」(「−」)號；(2) 若[n + k, n − k] (1 ≤ k ≤ n)位置取「+」(「−」)號，則該位置所在一「列」中由該位置起向下全取「+」(「−」)號；(3) 若[n − k, n + k] (1 ≤ k ≤ n)位置取「+」(「−」)號，則該位置所在一「行」中由該位置起向下全取「+」(「− 」)號。下圖顯示「一階可定義限定詞」的「數字三角形」特徵：

我們可以把上述(1)－(3)中取「+」號的範圍表達為合取三分結構式。此外，「第0對角線」至「第2n − 1對角線」上的「+」號位置也可以逐一表達為合取三分結構式。請注意上述各個「+」號範圍／位置互不重疊，所以最後我們可以用「∨」把上述各個合取三分結構式連起來，從而得到Q的表達式。由於上述各個合取三分結構式代表的「+」號範圍／位置都具有「左連續限定詞」的「數字三角形」特徵，至此證得Q可被表達為有限個「左連續限定詞」的析取。

以上圖為例，我們把該圖代表的限定詞稱為Q，並把該圖分解為下圖所示的六個互不重疊的範圍：

由於上述範圍由有限個孤立的點和呈規律性的範圍組成，我們可以把這些點和範圍逐一表述為合取三分結構式，然後用「∨」把各個合取三分結構式連結起來，便可得到Q的表達式如下：

((at least 2)(A)(B) ∧ (at least 2)(A)(~B))
∨ (no(A)(B) ∧ (at least 4)(A)(~B))
∨ ((at least 4)(A)(B) ∧ no(A)(~B))
∨ (no(A)(~B) ∧ (exactly 1)(A)(B))
∨ ((exactly 1)(A)(~B) ∧ (exactly 1)(A)(B))
∨ ((exactly 1)(A)(~B) ∧ (exactly 2)(A)(B))

請注意上述六個合取三分結構式所代表的圖形都具有「左連續限定詞」的「數字三角形」特徵，所以這六個三分結構式都表達「左連續限定詞」，由此可見Q可表達為有限個「左連續限定詞」的析取。

「定理5」和「定理6」告訴我們，「一階可定義性」與「左連續性」有密切關係。可是，這兩條定理對於證明某些限定詞的「一階不可定義性」卻不甚方便。舉例說，雖然我們知道"(an even number of)"、 "(an odd number of)"以及很多「右比例限定詞」和「右補右比例限定詞」不是「左連續」的，但要證明它們不能表達為有限個「左連續限定詞」的析取，卻似乎不是簡單的事。對於定義於無限論域上的限定詞(例如"(infinitely many)")，這兩條定理就更加是無能為力。不過，我們還有其他方法證明上述這些限定詞的「一階不可定義性」，這將留待下文再作介紹。

4.4 類可歸約性、存在性與一階可定義性的關係

根據「定理2」和「定理3」，我們看到「類可歸約性」與「存在性」有以下關係：

EXIST ⊂ SR

此外，根據前面的討論，我們也看到「類可歸約性」與「一階可定義性」有一些共同之處，例如 "John's"以及很多「右比例限定詞」和「右補右比例限定詞」既不屬於SR，又不屬於FO-D。這裡說「很多」而非「全部」，是因為某些「右比例限定詞」(例如"some"、"no"等)和「右補右比例限定詞」(例如"every"、"(not every)"等)同時屬於SR和FO-D。不過，「類可歸約性」與「一階可定義性」是互相獨立的概念。一方面，我們有屬於SR但不屬於FO-D的限定詞，例如"(an even number of)"、"(all but an even number of)"等；另一方面，我們亦有屬於FO-D但不屬於SR的限定詞，例如"the"、"neither"等。現把「類可歸約性」、「存在性」與「一階可定義性」的關係總結成下圖(為免使上圖過於複雜，上圖沒有繪出↑MON和↓MON)：

5. 一階(量詞)可定義性

5.1 一階邏輯的推廣

儘管「一階邏輯」在現代數理邏輯中有很重要的地位，但自然語言中有很多常用限定詞不是「一階可定義」的。由此可見，「一階邏輯」的表達力相當有限。為了提高表達力，我們可以把「一階邏輯」推廣為「二階邏輯」 (Second Order Logic)。在「二階邏輯」下，謂詞或函項可以作為論元或量化的對象，例如 "most(A)(B)"便可以定義為(註8)：

∃f (f ∈ (A − B) → (A ∩ B) ∧ INJECTIVE(f) ∧ ~SURJECTIVE(f))

在上式中，f是函項變項，這個函項從(A − B)映射到(A ∩ B)，而且具有「內射」但卻無「滿射」的性質。這實際等於說|A − B| < |A ∩ B|，亦即"most(A)(B)"的集合論定義。

當然除了把「一階邏輯」推廣為「二階邏輯」這種「大手術」外，我們也可以對「一階邏輯」作一些小修補，辦法是在「一階邏輯」中加入新的量詞，從而把「一階邏輯」推廣為「一階(量詞)邏輯」(First Order (Quantifiers) Logic)。請注意這個名稱中的「量詞」是一個通稱，把不同量詞加入「一階邏輯」中，便可得到不同的「一階(量詞)邏輯」。當然，把新的量詞加入「一階邏輯」後，我們必須對「一階邏輯」原有的語形和語義部分作相應修改。以下用一個具體例子以作說明，設我們要把限定詞"most"加入「一階邏輯」中以得到FO(most)，那麼我們便要在原有語形部分的形成規則中增添以下規則：

若A和B是「謂詞變項」，x是「個體變項」，則most x (A(x), B(x))是「合式公式」。

相應地，原有語義部分的解釋函項也須增添以下條件：

||most x (A(x), B(x))|| = 1當且僅當|A ∩ B| > |A − B|，其中A = {a: ||A[a/x]|| = 1}，B = {a: ||B[a/x]|| = 1}。

我們還可以把多於一個的量詞加入「一階邏輯」，從而得到表達力更強的邏輯，其具體構造辦法只是前述辦法的簡單推廣。舉例說，如要把Q、Q'加入「一階邏輯」以得到FO(Q, Q')，我們只需在「一階邏輯」原有的形成規則和解釋函項中加入兩條與Q和Q'相關的規則和條件。為方便討論，我們可以把{Q、Q'}看成一個「序列」(註 9)，並用小寫字母來代表，例如把FO(Q, Q')記作FO(q)。

接著我們引入「一階(量詞)可定義性」(First Order (Quantifiers) Definability)(記作FO(q)-D) 的概念。設Q為限定詞、q為由限定詞組成的序列(這個序列可以只包含單個限定詞，也可以為空序列，我們規定 FO( ) = FO)，A、B為論元。我們說Q ∈ FO(q)-D當且僅當存在FO(q)-D上的語句p使得對任何語義模型M而言，

p在M中真 ⇔ Q(A)(B)在M中真

容易把上述定義推廣至任意類型量詞的情況。

接著引入邏輯系統的「表達力」(Expressive Power)的概念。設L和L'為兩個邏輯系統，我們說L不強於L' (記作L ≤ L')當且僅當對L中任何一個語句p而言，都有L'中的語句p'使得p ⇔ p'。基於以上定義，我們還可以定義以下概念：L等價於L' (記作L ≡ L')當且僅當L ≤ L' ∧ L' ≤ L；L弱於L' (記作L < L')當且僅當L ≤ L' ∧ L' ~≤ L；L與L'不可比較(Incomparable)(記作L <> L')當且僅當L ~≤ L' ∧ L' ~≤ L。容易看到，以上定義的「≤」是一個「偏序」(Partial Order)，即滿足「自反性」、「反對稱性」和「傳遞性」。

我們可以透過以下定理(證明從略)把上述「可定義性」與「表達力」的概念聯繫起來。

定理7：設q和q'為兩個量詞序列，FO(q) ≤ FO(q')當且僅當對q中任何成員Q而言，都有Q ∈ FO(q')-D。

根據以上定義和定理，容易推出以下定理：

定理8：	設q、q'、q''為量詞序列，
	(i) FO(q) ≤ FO(q, q')
	(ii) 設FO(q) ≤ FO(q')，若對q''中任何成員Q''，Q'' ∈ FO(q)-D，則Q'' ∈ FO(q')-D
	(iii) 設FO(q) ≤ FO(q')，若對q'中任何成員Q'，Q' ∈ FO(q'')-D，則對q中任何成員Q，Q ∈ FO(q'')-D

以下只證(iii)以作示範，設FO(q) ≤ FO(q')，並設對q'中任何成員Q'，Q' ∈ FO(q'')-D，那麼根據「定理7」，FO(q') ≤ FO(q'')。根據「≤」的「傳遞性」，有FO(q) ≤ FO(q'')，由此再根據「定理7」，(iii)的結論成立。

5.2 可定義性的證明

當代廣義量詞理論的一個研究課題是比較不同「一階(量詞)邏輯」之間「表達力」的強弱。根據「定理7」，這等同於比較量詞在各種「一階(量詞)邏輯」上的「可定義性」。我們首先引入以下定理。

定理9：設q、q'為量詞序列，FO(q) ≡ FO(q, q')當且僅當對q'中任何成員Q'而言，Q' ∈ FO(q)-D。

根據「定理8(i)」，FO(q) ≤ FO(q, q')，所以我們可以把上述定理中「當且僅當」左面的式子弱化為FO(q, q') ≤ FO(q)。此外，對於q中任何成員Q而言，都必然有Q ∈ FO(q)-D，所以我們不妨把上述定理中「當且僅當」右面的式子強化為「對序列{q, q'}中任何成員Q*而言，都有Q* ∈ FO(q)-D」。經此修改後，上述定理變成

FO(q, q') ≤ FO(q)當且僅當對序列{q, q'}中任何成員Q*而言，都有Q* ∈ FO(q)-D。

但根據「定理7」，這顯然是成立的，本定理得證。

「定理9」告訴我們，如果我們把在FO(q)可定義的量詞加入FO(q)中，所得邏輯系統等價於原來的FO(q)。利用此一定理以及前面有關「一階可定義性」的結果，我們馬上得到一些結果，例如：

FO((at least 3), (at most 2), the) ≡ FO

接著我們有以下定理。

定理10：	(i) FO(Q₀) ≤ FO(I) ≤ FO(MO)
	(ii) FO(Q^R) ≤ FO(most) ≤ FO(MO)
	(iii) FO(MO) ≤ FO(Q^H)
	(iv) FO(Q_even) ≤ FO(Q^H)

為方便以下證明，這裡首先給出上列某些量詞的真值條件(在以下定義中，A、B為集合，R為四元謂詞，f、g為把U映射到U的函項)：

Q₀(A) ⇔ A有無窮多個元素
I(A)(B) ⇔ |A| = |B|
MO(A)(B) ⇔ |A| > |B|
Q^R(A) ⇔ |A| > |~A|
Q^H(R) ⇔ ∃f∃g∀x∀y (R(x, f(x), y, g(y))
Q_even(A) ⇔ |A|為偶數

首先考慮(i)的前半部。根據「無窮大」的特性，若集合A有無窮多個元素，那麼從A剔除任意一個元素x，所得集合仍有無窮多個元素。由此我們有

Q₀(A)	⇔ ∃x (A(x) ∧ \|A\| = \|A − {x}\|)
	⇔ ∃x (A(x) ∧ \|{y: A(y)}\| = \|{y: A(y) ∧ y ≠ x}\|)
	⇔ ∃x (A(x) ∧ Iy (A(y), A(y) ∧ y ≠ x))

由於上面最後一式只用到「一階邏輯」的語言以及量詞I，屬於FO(I)中的語句，我們有Q₀ ∈ FO(I)-D，由此根據「定理7」，(i)的前半部得證。

(i)的後半部可證明如下：

I(A)(B)	⇔ \|A\| ≤ \|B\| ∧ \|B\| ≤ \|A\|
	⇔ ~MOx (A(x), B(x)) ∧ ~MOx (B(x), A(x))

由此可見I ∈ FO(MO)-D，根據「定理7」，(i)的後半部得證。

(ii)的前半部可證明如下：

Q^R(A)	⇔ \|A\| > \|~A\|
	⇔ most(U)(A)
	⇔ most({x: x = x})({x: A(x)})
	⇔ most x (x = x, A(x))

由此可見Q^R ∈ FO(most)-D，根據「定理7」，(ii)的前半部得證。

(ii)的後半部可證明如下：

most(A)(B)	⇔ \|A ∩ B\| > \|A − B\|
	⇔ MO(A ∩ B)(A − B)
	⇔ MOx (A(x) ∧ B(x), A(x) ∧ ~B(x))

由此可見most ∈ FO(MO)-D，根據「定理7」，(ii)的後半部得證。

接著考慮(iii)，我們首先從MO的否定入手，

~MO(A)(B) ⇔ |A| ≤ |B|

根據集合論，|A| ≤ |B|當且僅當存在一個從A映射到B的「內射」(亦即「一一函數」)。由於我們在這裡要定義從U映射到U的函項，我們把上式右端改寫為(註10)

∃f∀x∀y ((x = y ⇔ f(x) = f(y)) ∧ (A(x) ⇒ B(f(x))))

由於兩個函數f和g相等當且僅當對所有元素x，f(x) = g(x)，我們可以把上式進一步改寫為

∃f∃g∀x∀y ((x = y ⇔ f(x) = g(y)) ∧ (A(x) ⇒ B(f(x)))) (10)

現在如果定義

R(x, z, y, w) = (x = y ⇔ z = w) ∧ (A(x) ⇒ B(z)))

並把上式代入Q^H的真值條件，那麼(10)便等同於Q^H(R(x, z, y, w))。綜合以上討論，我們有

MO(A)(B) ⇔ ~Q^H(R(x, z, y, w))

由此可見MO ∈ FO(Q^H)-D，根據「定理7」，(iii)得證。

最後考慮(iv)，我們作以下推理：|A|為偶數當且僅當存在一個「內射」f，使得f(x) = y ⇔ f(y) = x，並且x ∈ A ⇔ f(x) ≠ x (註11)。基於上述討論，我們有

Q_even(A)	⇔ \|A\|為偶數
	⇔ ∃f∃g∀x∀y ((x = y ⇔ f(x) = g(y)) ∧ (f(x) = y ⇔ g(y) = x) ∧ (A(x) ⇔ x ≠ f(x)))
	⇔ Q^H(R(x, z, y, w))

其中

R(x, z, y, w) = (x = y ⇔ z = w) ∧ (z = y ⇔ w = x) ∧ (A(x) ⇔ x ≠ z)

由此可見Q_even ∈ FO(Q^H)-D，根據「定理7」，(iv)得證。

我們還有以下等價關係。

定理11：	(i) FO(MO) ≡ FO(Q₀, most)
	(ii) FO(MO) ≡ FO(more ... than ...)

以下證明(i)。首先，根據「定理10」，Q₀和most都屬於FO(MO)-D，因此根據「定理7」， FO(Q₀, most) ≤ FO(MO)。接著考慮MO的「可定義性」。當A ∩ B為有限集合時，我們有

\|A\| > \|B\|	⇔ \|A − B\| + \|A ∩ B\| > \|B − A\| + \|A ∩ B\|
	⇔ \|A − B\| > \|B − A\|

當A ∩ B為無限集合時，我們有

|A| = max(|A − B|, |A ∩ B|)
|B| = max(|B − A|, |A ∩ B|)

由此必然有

|A| > |B| ⇔ (|A − B| > |B − A|) ∧ (|A − B| > |A ∩ B|)

綜合以上討論，我們有

MO(A)(B)	⇔ \|A\| > \|B\|
	⇔ (\|A − B\| > \|B − A\|) ∧ (Q₀(A ∩ B) ⇒ \|A − B\| > \|A ∩ B\|)
	⇔ (most((A − B) ∪ (B − A))(A)) ∧ (Q₀(A ∩ B) ⇒ most(A)(~B))
	⇔ (most x ((A(x) ∧ ~B(x)) ∨ (B(x) ∧ ~A(x)), A(x))) ∧ (Q₀x (A(x) ∧ B(x)) ⇒ most x (A(x), ~B(x)))

由此可見MO ∈ FO(Q₀, most)-D，根據「定理7」，FO(MO) ≤ FO(Q₀, most)。綜合以上結果，(i)乃得證。

接著證明(ii)。首先，由於

(more ... than ...)(A, B)(C)	⇔ \|A ∩ C\| > \|B ∩ C\|
	⇔ MO(A ∩ C)(B ∩ C)
	⇔ MOx (A(x) ∧ C(x), B(x) ∧ C(x))

可見(more ... than ...) ∈ FO(MO)-D，根據「定理7」，FO(more ... than ...) ≤ FO(MO)。其次，由於

MO(A)(B)	⇔ \|A\| > \|B\|
	⇔ (more ... than ...)(A, B)(U)
	⇔ (more ... than ...)x (A(x), B(x), x = x)

可見MO ∈ FO(more ... than ...)-D，根據「定理7」，FO(MO) ≤ FO(more ... than ...)。綜合以上結果，(ii)乃得證。

5.3 不可定義性的證明

要證明量詞Q在邏輯系統FO(q)下不可定義，傳統的方法是利用某些較艱深的元邏輯性質。不過，Peters和 Westerstahl在Quantifiers in language and logic一書中介紹了一套基於「博奕論」(Game Theory) 的理論，對於證明<1>型量詞的「一階不可定義性」極為簡便，以下筆者將這種證明方法概括為以下定理(證明從略)。

定理12：	設Q為<1>型量詞，以下方法可證明Q ∈ ~FO-D。對任何自然數n，找出兩個論域U和U'以及集合A ∈ U、A' ∈ U'使得
	(1) 若\|A\| < n或\|A'\| < n，則\|A\| = \|A'\|。若\|~A\| < n或\|~A'\| < n，則\|~A\| = \|~A'\|。
	(2) Q_U(A) ~⇔ Q_U'(A')。

現在讓我們利用上述方法來證明以下定理。

定理13：Q₀, (p / q), Q^R, Q_even ~∈ FO-D，其中p、q為自然數，p < q並且

(p / q)(A) ⇔ |A| / |U| > p / q

首先考慮Q₀，對任何自然數n，我們可以構造以下模型：

在上述模型中，|A| > |A'| ≥ n，|~A| = |~A'|，而且(Q₀)_U(A)並且 ~(Q₀)_U'(A')，由此根據「定理12」，Q₀ ~∈ FO-D。

其次考慮(p / q)，我們可以構造以下模型：

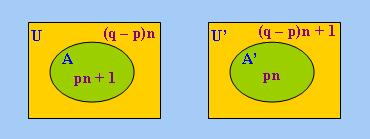
在上述模型中，|A|、|A'|、|~A|和|~A'|都大於n。此外，由於(pn + 1) / (qn + 1) > p / q並且pn / (qn + 1) ≤ p / q，我們有(p / q)_U(A)並且~(p / q)_U'(A')，由此根據「定理12」，(p / q) ~∈ FO-D。由於Q^R = (1 / 2)，我們亦有Q^R ~∈ FO-D。

最後考慮Q_even，我們可以構造以下模型：

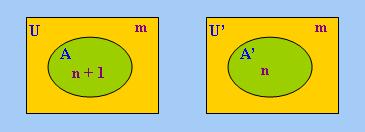
在上述模型中，|A| > |A'| ≥ n，|~A| = |~A'|，而且由於n與n + 1具有不同的奇偶性， (Q_even)_U(A) ~⇔ (Q_even)_U'(A')，由此根據「定理12」，Q_even ~∈ FO-D。

「定理13」中的量詞都是<1>型量詞，但我們可以透過以下的「關係化」操作把<1>型量詞轉化為限定詞：

(Q^rel)_U(A)(B) ⇔ Q_A(A ∩ B) (11)

從上述定義可推出以下關係：

(Q₀)^rel = (infinitely many)
(p / q)^rel = (more than p / q)
(Q^R)^rel = most
(Q_even)^rel = (an even number of)

<1>型量詞及其「關係化」在「表達力」的強弱上有以下關係：

定理14：設Q為<1>型量詞，則FO(Q) ≤ FO(Q^rel)。

根據《廣義量詞系列：量詞的普遍性質與操作》中的式(33)，我們可以作以下推導：

Q(A)	⇔ Q^rel(U)(A)
	⇔ Q^relx (x = x, A(x))

由此證得Q ∈ FO(Q^rel)-D。根據「定理7」，本定理得證。

透過上述「關係化」操作和前述某些定理，容易推得

定理15：(infinitely many), (more than p / q), more, (an even number of) ~∈ FO-D

以下只證"(more than p / q)"的情況以作示範。根據「定理14」以及上述關係，我們有 FO((p / q)) ≤ FO(more than p / q)。由此根據「定理13」以及「定理8(iii)」的逆否命題，我們可以從(p / q) ~∈ FO-D推出(more than p / q) ~∈ FO-D。由此可見，很多「右比例限定詞」都是「一階不可定義」的。此外，由於「右比例限定詞」往往可以用「右補右比例限定詞」來定義，例如

(more than p / q)(A)(B) ⇔ ~(all but at most p / q)(A)(~B)

由此可以推斷很多「右補右比例限定詞」也是「一階不可定義」的。

5.4 一階(量詞)邏輯的層級

在上一小節筆者利用「定理12」所述的「博奕論」方法證明了某些量詞在「一階邏輯」下是不可定義的，原則上我們可以把這種方法加以推廣，用來證明某些量詞在某些「一階(量詞)邏輯」下是不可定義的，但其證明方法較「定理12」牽涉更多複雜的概念，所以以下定理只列出這些結果，證明從略。

定理16：	(i) I ~∈ FO(Q₀)-D
	(ii) most ~∈ FO(Q^R)-D
	(iii) Q₀ ~∈ FO(most)-D；Q₀ ~∈ FO(Q_even)-D
	(iv) Q^R ~∈ FO(I)-D；Q^R ~∈ FO(Q_even)-D
	(v) Q_even ~∈ FO(MO)-D

請注意從上述定理，我們還可以推出更多否定關係。舉例說，從Q₀ ~∈ FO(most)-D以及「定理10(ii)」和「定理8(ii)」，可推出Q₀ ~∈ FO(Q^R)-D。此外，從 Q₀ ~∈ FO(most)-D以及「定理10(i)」和「定理8(iii)」，亦可推出I ~∈ FO(most)-D，等等。

利用前述各個定理，我們可以得到各種「一階(量詞)邏輯」之間的「<」和「<>」關係。舉例說，根據「定理 10(i)」的前半部、「定理16(i)」以及「定理7」，可以得到FO(Q₀) < FO(I)。此外，根據上段所述的推理方法，我們可以從Q^R ~∈ FO(I)-D推出Q^R ~∈ FO(Q₀)-D。把此一結果與Q₀ ~∈ FO(Q^R)-D結合，並再利用「定理7」，便可得到FO(Q₀) <> FO(Q^R)。

最後，我們還要考慮Q與Q^rel之間的「≡」關係。根據「定理14」，如果

FO(Q^rel) ≤ FO(Q) (12)

那麼便必有FO(Q^rel) ≡ FO(Q)。我們把(12)稱為「關係化性質」(Relativization Property)(記作REL)，很多<1>型量詞都具有這種性質，例如從以下關係：

(infinitely many)(A)(B) ⇔ Q₀x (A(x) ∧ B(x))
(an even number of)(A)(B) ⇔ Q_evenx (A(x) ∧ B(x))
every(A)(B) ⇔ ∀x (A(x) ⇒ B(x))

容易推出

FO(infinitely many) ≡ FO(Q₀)
FO(an even number of) ≡ FO(Q_even)
FO(every) ≡ FO(∀) ≡ FO

請注意並非所有<1>型量詞都屬於REL，舉例說，根據「定理16(ii)」，FO(most) ~≤ FO(Q^R)，即Q^R ~∈ REL。

把上述種種「≡」、「<」和「<>」關係綜合起來，便可得到如下圖所示的「一階(量詞)邏輯」層級：

上圖列出了八個(互不等價的)邏輯系統，各個系統可被看成區域，它們之間的連線可被看成路徑，如果存在一條從左到右的路徑把某區域FO(q)連接至另一區域FO(q')，則FO(q) < FO(q')。如果兩個區域FO(q)與FO(q')之間沒有上述路徑連接，則FO(q) <> FO(q')。

6. 與單調量詞相關的可定義性

6.1 遞增量詞

由於單調量詞(尤其是(右)遞增量詞)在自然語言中有很重要的地位，一個很自然的研究課題是，哪些量詞可被 FO(q)定義，其中q為由遞增量詞組成的序列。為方便以下討論，首先引入一些概念。設Q為「有限論域數量遞增 <1>型量詞」，那麼Q的「數字三角形」上每一條「對角線」要麼全為「−」號，要麼從某一位置起向右全為「+」號。因此Q相當於一個依賴於函數f的量詞Q_f，使得(註12)

(Q_f)_U(A) ⇔ |A| ≥ f(|U|) (13)

並且f為把非負整數映射為非負整數的函數，滿足0 ≤ f(n) ≤ n + 1，f稱為「單調性函數」 (Monotonicity Function)。

根據《廣義量詞系列：量詞的普遍性質與操作》的「定理3」，若限定詞Q ∈ CONS_r ∩ EXT，則存在<1>型量詞Q'使得Q = (Q')^rel，因此我們可以利用「關係化」把上述定義推廣至「有限論域邏輯右遞增限定詞」。設Q ∈ LOG ∩ FIN，Q'為與之相關的 <1>型量詞，那麼Q ∈ MON↑當且僅當存在一個函數f使得0 ≤ f(n) ≤ n + 1，並且Q = (Q'_f)^rel，其中

((Q'_f)^rel)_U(A)(B)	⇔ (Q'_f)_A(A ∩ B)	(根據(11))
	⇔ \|A ∩ B\| ≥ f(\|A\|)	(根據(13)) (14)

上述定義的實質是把「遞增<1>型量詞」和「右遞增限定詞」分別表述為Q_f和 Q_f^rel，由此我們有兩種「可定義性」：FO(q_f)-D和 FO(q_f^rel)-D，其中q_f和q_f^rel分別代表由所有形如Q_f和Q_f^rel的量詞組成的序列，而且0 ≤ f(n) ≤ n + 1。

以下是上述定義的一些例證。設f(n) = k (k為大於0的整數)，那麼Q_f = ∃_≥k，Q_f^rel = (at least k)。另設f'(n) = n + 1，那麼由於不可能有|A| ≥ |U| + 1或|A ∩ B| ≥ |A| + 1，Q_f'和 Q_f'^rel恆假，即都等於0。

接著引入「有界波動性」(Bounded Oscillation)(記作BO)的概念。在「數字三角形」上，我們把每一條「對角線」上「+／−」號的變化次數稱為「波動數」(Oscillation)。我們說量詞Q是「有界波動」的當且僅當存在一個「波動上界」m (m為非負整數)，使得每一條「對角線」的「波動數」都不大於m。

根據上述定義，容易看到

MON↑ ∪ MON↓ ⊆ BO

這是因為單調量詞每一條「對角線」上的「+／−」號最多只變化一次，即m = 1。由此可見，「有界波動性」是「單調性」的推廣。某些非單調量詞也可以是「有界波動」的，以∃_{(≥ 1 ∧ ≤ 3)
∨ > 5}為例，從其「數字三角形」可見m = 3：

當然也有一些量詞不是「有界波動」的，以Q_even為例，它的「第i對角線」上的「波動數」恰好等於i，即隨著i而無限遞增，因此這個量詞不屬於BO。

Vaananen在Unary Quantifiers on Finite Models一文中提出以下定理(證明從略)：

定理17：在Q<1>(即由<1>型量詞組成的論域)下，BO = FO(q_f)-D。

舉例說，我們有

∃_{(≥ 1 ∧ ≤ 3) ∨ > 5}(A) ⇔ (Q_fx (A(x)) ∧ ~Q_gx (A(x))) ∨ Q_hx (A(x))

其中f(n) = 1，g(n) = 4，h(n) = 6。由於Q_even ~∈ BO，由「定理17」可知 Q_even ~∈ FO(q_f)-D。

對於限定詞，我們首先有以下結果：

定理18：在DET (即由限定詞組成的論域)下，LOG ∩ INT ⊆ FO(q_f^rel)-D。

設Q ∈ LOG ∩ INT，根據《廣義量詞系列：單調性的進階研究》中對INT的表述，存在一個由非負整數組成的集合S，使得Q(A)(B) ⇔ |A ∩ B| ∈ S。接著定義以下函數：

f(n) =	1，若n ∈ S
	2，若n ~∈ S

若0 ∈ S，

Q(A)(B)	⇔ \|A ∩ B\| ∈ S
	⇔ 1 ≥ f(\|A ∩ B\|)	(根據f的定義)
	⇔ (A ∩ B = Φ) ∨ ∃x (x ∈ A ∩ B ∧ \|{x}\| ≥ f(\|A ∩ B\|))
	⇔ (A ∩ B = Φ) ∨ ∃x (x ∈ A ∩ B ∧ Q_f^rel(A ∩ B)({x}))	(根據(14))
	⇔ ~∃x (A(x) ∧ B(x)) ∨ ∃x (A(x) ∧ B(x) ∧ Q_f^rely (A(y) ∧ B(y), y = x))

若0 ~∈ S，則從上面第二行不能推出A ∩ B = Φ，因此只需把A ∩ B = Φ (及其一階邏輯表達式)從上面推理中刪去即可。由於(an even number of) ∈ INT，由「定理18」可知(an even number of) ∈ FO(q_f^rel)-D。

為加強「定理18」，我們首先引入「著色函數」(Colouring Function)的概念。一個「著色函數」c就是把非負整數映射到「顏色」集合C的函數，其中C可為任意有限集合。對於非負整數有序對[x, y]，我們規定

c([x, y]) = [c(x), c(y)]

在上述定義下，「數字三角形」上的每個位置都對應著一個「顏色對」，我們把所有相同的「顏色對」歸入一個「顏色類」(Colour Class)。舉例說，設

c(n) =	r，若n為偶數	(15)
	g，若n為奇數

那麼我們便有四個「顏色類」，它們在「數字三角形」上的分佈如下圖所示：

接著我們便可以定義「有界色波動性」(Bounded Colour Oscillation)(記作BCO)的概念，我們說量詞Q是「有界色波動」的當且僅當存在一個「著色函數」c和「波動上界」m，使得每一條「對角線」上每一個「顏色類」內的「波動數」都不大於m。

根據上述定義，容易看到

BO ⊆ BCO

這是因為我們只需採用以下「常值著色函數」便可：

c(n) = r

此外，BCO還包含某些不屬BO的量詞，以"(an even number of)"為例，我們可以取前述的函數(15)作為「著色函數」。現在如果把「數字三角形」上各位置的「+／−」號與所屬「顏色類」並列如下：

那麼容易看到，每一條「對角線」上每一個「顏色類」的「+／−」號都不變，即「波動數」恆等於0。

上述例子顯示BCO包含很多量詞，那麼究竟有沒有不屬BCO的量詞？Vaananen和Westerstahl在On the Expressive Power of Monotone Natural Language Quantifiers over Finite Models一文中提出以下「數字三角形」所代表的量詞不屬BCO (證明從略)：

上圖具有以下特點：在「第2^k對角線」(k ≥ 1)上，「+／−」號交替變化；在「第 2^k − 1對角線」上，「+／−」號每兩個位置變化一次；在「第 2^k − 2對角線」上，「+／−」號每三個位置變化一次，如此類推，直至「第 2^k−1對角線」又回復至「+／−」號交替變化。Vaananen和Westerstahl還提出了以下定理(證明從略)：

定理19：在DET下，BCO = FO(q_f^rel)-D。

如前所述，(an even number of) ∈ BCO，由「定理19」可知(an even number of) ∈ FO(q_f^rel)-D，這與前面的結果吻合。

6.2 光滑量詞

筆者在《廣義量詞系列：單調性的進階研究》中介紹了「光滑性」(記作 SMO)的概念，由此我們可以研究哪些量詞可被FO(q)定義，其中q為由光滑量詞組成的序列。由於「光滑性」是比「遞增性」更強的性質，上述研究的結果將會收窄「定理17和19」中可定義量詞的範圍。跟上一小節一樣，我們首先把光滑量詞轉化為另一種形式。設Q為「有限論域數量光滑<1>型量詞」，那麼Q的「數字三角形」有以下特徵：

容易看到上圖有遞增量詞的特徵(這是因為SMO ⊆ MON↑)，因此我們可以把Q表述為Q_F，其中F為滿足0 ≤ F(n) ≤ n + 1的函數並且Q_F的定義同(13)。請注意F的值與上圖具有以下對應關係：若F(n) = n + 1，這代表上圖的「第n對角線」全為「−」號；若F(n) = k < n + 1，這代表「第n對角線」上最左的「+」號位於[n − k, k]。從上圖還可以看到，若「第n對角線」上最左的「+」號位於[n − k, k]，則「第n + 1對角線」上最左的「+」號要麼位於其緊鄰的左下方(即[n + 1 − k, k])，要麼位於其緊鄰的右下方(即[n − k, k + 1])。換句話說，函數F滿足

F(n) ≤ F(n + 1) ≤ F(n) + 1 (16)

跟上一小節類似，我們也可以透過「關係化」把上述定義推廣至「有限論域邏輯限定詞」。設Q ∈ LOG ∩ FIN，Q'為與之相關的<1>型量詞，那麼Q ∈ SMO當且僅當存在一個滿足0 ≤ F(n) ≤ n + 1以及(16)的函數F，使得Q = (Q'_F)^rel，其中(Q'_F)^rel的定義同 (14)。類似遞增量詞，對於光滑量詞來說，我們也有兩種「可定義性」：FO(q_F)-D和 FO(q_F^rel)-D，其中F須滿足前述條件。

不過，學界當前尚未圓滿解決上述兩種「可定義性」問題，只得到一些局部結果，以下是Vaananen和 Westerstahl提出的一個結果(證明從略)：

定理20：在DET下，FO(q_F^rel)-D ⊆ BO。

根據前面的討論，由於"(an even number of)"不屬BO，由此可知這個限定詞也不屬 FO(q_F^rel)-D。

請注意「定理20」中的「⊆」實際是「真包含關係」(即「⊂」)，即存在屬於BO但不屬 FO(q_F^rel)-D的限定詞，例如以下限定詞

(some or none of an even number of)(A)(B) ⇔ |A|為偶數

便屬於BO (其「數字三角形」上每條「對角線」要麼全為「+」號，要麼全為「−」號，即「波動數」恆等於0)，但卻不屬於FO(q_F^rel)-D (證明從略)。

註1：由於對任何論元，1恆取真值，所以不管A、B、C、D滿足何種條件，都有1(A)(B) ⇔ 1(C)(D)，因此1 ∈ INT ∩ RC-INT。同理，由於對任何論元，0恆取假值，所以必有0(A)(B) ⇔ 0(C)(D)，因此0 ∈ INT ∩ RC-INT。此外，根據《廣義量詞系列：單調性的進階研究》，若Q ∈ INT ∩ RC-INT，其「數字三角形」表現為，三角形上若有某位置取「+」號，則該位置所在的「行」和「列」全取「+」號，即整個三角形都取「+」號，這意味著Q ∈ {1, 0}。綜合以上結果，我們有INT ∩ RC-INT = {1, 0}。

註2：因此之故，Keenan把「相交限定詞」和「右補相交限定詞」分別稱為「廣義存在限定詞」(Generalized Existential Determiner)和「廣義全稱限定詞」(Generalized Universal Determiner)。

註3：如果「存在句」的形式為「There + be + Q + A」(即沒有「後續成分」B)，其語義則等同於Q(A)(U)。

註4：根據《廣義量詞系列：量詞的代數性質》的「定理11(i)」，「基數限定詞」是「相交限定詞」的次類。

註5：以下對"the"的定義跟《廣義量詞系列：基本單式量詞》中的定義不同。在上述網頁中，"the"被處理成「部分函項」，而且其定義包含「語境集」X。為簡化討論，本文沿用Russell對"the"的定義。

註6：事實上，代表集合基數的符號| |是集合論而非一階邏輯的符號。請注意即使是與集合基數直接相關的限定詞，在一階邏輯中也並非直接使用| |來定義，而是採取「迂迴」的手法，例見前述"(at least 3)" 和"(at most 2)"的一階邏輯表達式。

註7：在某些情況下，(7)中的某個「析取項」可以不出現。此外，當(7)中的數字n或m為0時，我們一般使用 "no"而不說"(at most 0)"。另請注意，"(at most m)(A)(~B)"亦可以表達為"(all except at most m)(A)(B)"。

註8：在下式中，INJECTIVE(f)和SURJECTIVE(f)可分別看成命題「f有內射性質」和「f有滿射性質」的簡寫，這兩個命題都可以根據集合論的定義重新表述為「二階邏輯」的表達式，例如INJECTIVE(f)便可以表達為 ∀x∀y (x ≠ y ⇒ f(x) ≠ f(y))。

註9：因此嚴格地說，FO(Q, Q')應寫成FO({Q, Q'})，但為免引入過多括號，本文不採用這種寫法。

註10：舉例說，如果U = {x, y, z, u, v, w}，A = {x, y}，B = {z, u, v}，那麼f可以定義如下：f(x) = z ，f(y) = u，f(z) = x，f(u) = y，f(v) = v，f(w) = w。

註11：舉例說，如果U = {x, y, z, u, v}，A = {x, y, z, u}，那麼f可以定義如下：f(x) = z，f(y) = u， f(z) = x，f(u) = y，f(v) = v。

註12：請注意在<1>型量詞的「數字三角形」上，[x, y]中的x和y分別代表|U − A|和|A|，而x + y = |U|。

返回語言學專題