Números Complejos

Los números de la forma z = a+bi, donde a, b son números reales, y ademas i es la unidad imaginaria, siendo i² = - 1,se denominan números complejo. La parte formada por a se la denomina parte real de z, y a la formada por b parte imaginaria de z.

Representación de los números complejos

Ejemplo: el número complejo z = -3+2i esta representado por el punto de coordenadas (-3,2).

Operaciones con números complejos

Suma

Sea z y w números complejos, donde z = a+bi y w=c+di

z+w = (a+bi) + (c+di) = (a+c) + (b+d) i

Ejemplo : sean z = -3+4i y w = 1+2i.

(-3+4i) + (1+2i) = (-3+1) + (4+2)i = -2+6i

Multiplicación

Sea z y w números complejos, donde z = a+bi y w=c+di

z*w = (a+bi)*(c+di) = (a*c - b*d) + (a*d + b*c)i

Ejemplo: z = 2+3i y w = 1-4i

(2+3i)*(1-4i) = (2*1 - 3*(-4)) + (2*(-4) + 3*1)i = 14-5i

División

Sea z y w números complejos, donde z = a+bi y w = c+di, y w' cojugado de w, es decir w' = c-di

(a+bi)/(c+di) = (a+bi)*(c-di)/(c+di)*(c-di) = ((a*c+b*d) - (a*d-b*c)i)/(c*c+d*d)

Ejemplo: z = 2+i y w = 3+2i

(2+i)/(3+2i) = ((2+i)*(3-2i))/((3+2i)*(3-2i)) = 8-i/13

Norma

Sea z = a+bi, llamaremos norma de z a

|z|² = a*a + b*b

Ejemplo: z = 3-2i

|z|² = 9 + 4 = 13

Valor absoluto o módulo

Llamaremos valor absoluto de z, a

|z| = (a*a + b*b)^1/2

Ejemplo: z = 3-2i

|z| = (9 + 4)^1/2 = 13^1/2 = 3.6055..

Forma polar o forma trigonométrica

Un número complejo z = a+bi, se puede escribir en la forma trigonometrica.

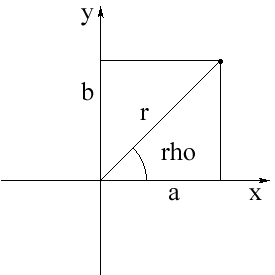
z = r*(cos(rho) + i sin(rho))

donde r = |z| = (a*a + b*b)^1/2 es la distancia desde el punto al origen.

rho = arctg(b/a)

rho es el argumento de z, es el ángulo que forma con el eje x.

La siguiente rutina convierte un número complejo de la forma binomica Z = x + yi a la trigonométrica, devolviendo r y el argumento en este caso lo llame theta

Sub Convercion(x As Double, y As Double, r As Double, theta As Double) If x = 0# Then If y = 0# Then r = 0# theta = 0# Else If y > 0# Then r = y theta = 0.5 * PI Else r = -y theta = -0.5 * PI End If End If Else r = Sqr(x * x + y * y) theta = Atn(y / x) If x < 0# Then If y >= 0# Then theta = PI + theta Else theta = -PI + theta End If End If End If End Sub

Potencia de un número complejo

Para hallar la potencia de un número complejo aplicamos el Teorema De Moivre, donde z = a+bi y n es número entero positivo.

zⁿ = rⁿ*(cos(n*rho) + i sin(n*rho))

donde r = |z| es el módulo y rho es el argumento de z.

La siguiente rutina halla la potencia de un nuúmero complejo Z = x + yi, elevado a una potencia N, la parte real y la imaginaria son retornados en los parametros a y b.

Function Power(x As Double, y As Double) As Double If x = 0# Then If y = 0# Then Power = 1# Else Power = 0# End If Else Power = Exp(Log(x) * y) End If End Function Sub FloatPower(x As Double, y As Double, a As Double, b As Double, N As Double) Dim r As Double Dim theta As Double Dim atmp, btmp As Double If (x * x + y * y) = 0# Then If N = 0# Then a = 1# b = 0# Else a = 0# b = 0# End If Else Convercion x, y, r, theta atmp = Power(r, N) btmp = theta * N End If a = atmp * Cos(btmp) b = atmp * Sin(btmp) End Sub