Ecuaciones Diferenciales Numéricas

Problema de Valor Inicial y Método de Euler

Las ecuaciones diferenciales aparecen naturalmente al modelar situaciones físicas en las ciencias naturales, ingeniería, y otras disciplinas, donde hay envueltas razones de cambio de una ó varias funciones desconocidas con respecto a una ó varias variables independientes. Estos modelos varían entre los más sencillos que envuelven una sola ecuación diferencial para una función desconocida, hasta otros más complejos que envuelven sistemas de ecuaciones diferenciales acopladas para varias funciones desconocidas. Por ejemplo, la ley de enfriamiento de Newton y las leyes mecánicas que rigen el movimiento de los cuerpos, al ponerse en terminos matemáticos dan lugar a ecuaciones diferenciales. Usualmente estas ecuaciones estan acompañadas de una condición adicional que especifica el estado del sistema en un tiempo o posición inicial. Esto se conoce como la condición inicial y junto con la ecuación diferencial forman lo que se conoce como el problema de valor inicial. Por lo general, la solucón exacta de un problema de valor inicial es imposible ó dificil de obtener en forma analítica. Por tal razón los métodos numéricos se utilizan para aproximar dichas soluciones. Comenzaremos discutiendo los métodos para ecuaciones escalares y luego generalizamos los mismos a sistemas de ecuaciones.

El Método de Euler

Primeramente consideraremos la ecuación diferencial de primer orden y su condición inicial :

y la formula de Euler (Método de Euler) :

Un ejemplo

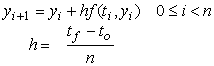
Usando el Método de Euler vamos a resolver la siguiente ecuación diferencial :

para comparar la solucion exacta es :

El algoritmo

La implementación en VisualC++ del Método de Euler es relativamente simple. Hacemos esto mediante una funcion llamada Metodo_Euler que recibe to (tinicial), tf (tfinal), yo (yinicial), n. Esta funcion devuelve dos vectores t[i] y y[i] con la solución aproximada.

void Metodo_Euler(double tinicial, double tfinal, double yinicial, int n)
{
 double h;
 int i;
 
 h=(tfinal-tinicial)/n;
 t[0]=tinicial;
 y[0]=yinicial;
 for (i=0; i<n; i++)
	{
	y[i+1]=y[i] + h*f(t[i], y[i]);
	t[i+1]=t[i] + h;
	}
}

Codigo Fuente

El siguiente ejemplo grafica la solucion exacta en color verde y la obtenida por el Metodo de Euler en blanco, click aqui para descargar el codigo fuente.

/*
 dy/dt = 1.0 - t + 4.0*y
 y(0.0) = 1.0
*/
#include <GL/glut.h>
#include <stdlib.h>
#include <stdio.h>
#include <math.h>

#define MAXPUNTOS	20

double y[MAXPUNTOS+1];
double t[MAXPUNTOS+1];

double f(double t, double y)
{
 return (1.0 - t + 4.0*y);
}

double exacta(double t)
{
 return (t/4.0 - 3.0/16.0 + (19.0/16.0)*exp(4.0*t));
}

void Metodo_Euler(double tinicial, double tfinal, double yinicial, int n)
{
 double h;
 int i;
 
 h=(tfinal-tinicial)/n;
 t[0]=tinicial;
 y[0]=yinicial;
 for (i=0; i<n; i++)
	{
	y[i+1]=y[i] + h*f(t[i], y[i]);
	t[i+1]=t[i] + h;
	}
}

void init(void)
{
 Metodo_Euler(0.0, 1.0, 1.0, MAXPUNTOS);
}

void display(void)
{
 int i;

 glClear(GL_COLOR_BUFFER_BIT);
 glMatrixMode( GL_MODELVIEW_MATRIX );
 glLoadIdentity();

 //grafica de la solucion exacta en color Verde
 glColor3f(0.0,1.0,0.0);  
 glBegin(GL_LINE_STRIP);
 for (i=0; i<MAXPUNTOS; i++)
 	 glVertex2f(t[i], exacta(t[i]));
 glEnd();

 //grafica de la solucion numerica en color Blanco
 glColor3f(1.0,1.0,1.0);
 glBegin(GL_LINE_STRIP);
 for (i=0; i<MAXPUNTOS; i++)
	 glVertex2f(t[i], y[i]);
 glEnd();

 glFlush ();
}

void reshape (int w, int h)
{
 if (!h)
	return;
 glViewport(0, 0, w, h);
 glMatrixMode(GL_PROJECTION);
 glLoadIdentity();
 gluOrtho2D(0.0, 1.0, 0.0, 40.0);
 glMatrixMode(GL_MODELVIEW);
 glLoadIdentity();
}

void keyboard(unsigned char key, int x, int y)
{
 switch (key) 
   {
   case 27: exit(0);
             break;
   }
}    

int main(int argc, char** argv)
{
 glutInit(&argc, argv);
 glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
 glutInitWindowSize (350, 350); 
 glutInitWindowPosition (0, 0);
 glutCreateWindow ("Metodo de Euler");
 init ();
 glutDisplayFunc(display); 
 glutReshapeFunc(reshape);
 glutKeyboardFunc(keyboard);
 glutMainLoop();
 return 0;
}