EL Método de Bisección

Para obtener una solución de f(x)=0 donde la función f(x) es continua, en el intervalo [a,b], donde f(a) y f(b) tienen diferente signo, es decir f(a).f(b)<0.

Ejemplo

A modo de ejemplo vamos a resolver la siguiente ecuación f(x)=Cos(x)-x=0, tomamos en a=0.5 y b=Pi/4, ya que f(0.5).f(Pi/4)<0, con TOL=0.000001 y N=20, y obtenemos una en raíz x=0.739085086..., que tiene una exactitud hasta la 6 cifra decimal.El código del ejemplo se encuentra en biseccion.zip (1.686 bytes)

Implementación del algoritmo

Entrada

• a : extremo inferior
• b : extremo superior
• Tol : tolerencia
• N : número máximo de iteraciones

Salida

• Res : retorna la solución de f(x)

Código

Sub Biseccion(ByVal a As Double, ByVal b As Double, ByVal TOL As Double, _
              ByVal N As Integer, ByRef res As Double)
Dim p, fa, fp As Double
Dim i As Integer
Dim Flag As Boolean

i = 1
fa = f(a)
Flag = False
Do While (i <= N) And Not (Flag)
    p = a + (b - a) / 2
    fp = f(p)
    If fp = 0 Or (b - a) / 2 < TOL Then
        res = p
        Flag = True
    End If
    i = i + 1
    If fa * fp > 0 Then
        a = p
        fa = fp
    Else
        b = p
    End If
Loop
If Not Flag Then
    MsgBox "El método fracaso por exceder el numero de iteraciones", vbExclamation, "Bisección"
End If
End Sub

Método de Regula Falsi

Nos permite encontrar la raíz de la ecuación f(x)=0, donde f(x) es una función continua definida en el intervalo [a,b], con f(a) y f(b) de signos diferentes.

Ejemplo

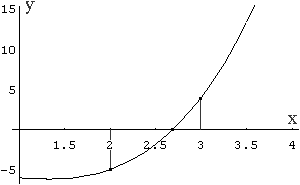
Encontrar las raíces de f(x)=x³-2x²-5=0, para ello necesitamos dos aproximaciones tomamos a=2 y b=3,ya que f(2)=-5 y f(3)=4, la tolerancia Tol=0.000001 y con N=10 iteraciones, obtenemos una raíz en x = 2.690647. Código en Visual Basic del ejemplo regula.zip (1.786 bytes)

Implementación del algoritmo

Entrada

• a : extremo inferior
• b : extremo superior
• Tol : tolerencia
• N : número máximo de iteraciones

Salida

• Flag : me devuelve True si tuvo exito y False en caso de haber superado el núumero de iteraciones, sin obtener la exactitud requerida.
• Res : retorna la solución de f(x)

Código

Sub Regula_Falsi(ByVal a As Double, ByVal b As Double, ByVal Tol As Double, _
                 ByVal N As Integer, ByRef Flag As Boolean, ByRef r As Double)
Dim q, q0, q1, p As Double
Dim i As Integer
i = 2
q0 = f(a)
q1 = f(b)
Do While (i <= N)
    p = b - q1 * (b - a) / (q1 - q0)
    If Abs(p - b) < Tol Then
        Flag = True
        r = p
        Exit Sub
    End If
    i = i + 1
    q = f(p)
    If (q * q1 < 0) Then
        a = b
        q0 = q1
    End If
    b = p
    q1 = q
    Flag = False
Loop
End Sub