Fuerza de friccion en fluidos

Fuerza de fricción en fluidos

Cuando un cuerpo se mueve a velocidad relativamente baja a través de un fluido tal como un gas o un liquido, la fuerza de fricción puede puede obtenerse aproximadamente suponiendo que es proporcional a la velocidad, y opuesta a ella. Por consiguiente escribimos

El coeficiente de fricción K depende de la forma del cuerpo. Por ejemplo, en el caso de una esfera de radio R, un cálculo laborioso indica que

relación conocida como la ley de Stokes. El coeficiente c depende de la fricción interna del fluido. Esta fricción interna se denomina también viscosidad y recibe el nombre de coeficiente de viscosidad.
El coeficiente de viscosidad de los liquidos disminuye a medida que aumenta la temperatura , mientras que en el caso de los gases , el coeficiente aumenta con el aumento de temperatura.

Cuando un cuerpo se cae a traves de un fluido viscoso bajo la acción de la la gravedad g, actuan sobre el las siguientes fuerzas

Si tomamos la direccion desde O hacia abajo como positiva, donde x es la distancia recorrida en funcion del tuempo, la ecuacion que describe su movimiento es

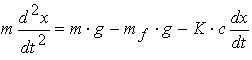
la que se puede escribir tambien como

donde m es la masa del cuerpo, como en esta ecuación tengo en cuenta el empuje ejercido por el fluido, de conformidad con el principio de Arquímides, es igual al peso del fluido desplazado por el cuerpo. Si mf es la masa del fluido desplazado, su peso es mf.g. Como el cuerpo es esferico de radio R, la masa del cuerpo m y la masa mf del fluido desplazado la podemos calcular con las siguientes formulas, d y df son respectivamente la densidad del cuerpo y del fluido

Para cuerpos grandes y velocidades mayores, la fuerza de fricción es proporcional a una potencia mayor de velocidad, esto lo trato en .

Código Fuente

Consideremos una pelota de plástico esferica que se deja caer desde una determinada altura, con una velocidad inicial v=0 m/s es decir parte de reposo. Supongamos que su masa es de m=78.3 g y su radio de R=15 cm. La densidad del aire es df=1.293 kg/m3 y su viscosidad es c=17.1 10-6 kg/m·s.

La siguiente grafica muestra tanto la solucion numerica en color verde, que tiene en cuenta la resistencia del fluido al movimiento, como asi tambien el empuje, en color azul esta la grafica de la trayectoria pero en el vacio, el intervalo calculado es de un segundo, como se puede ver en ausencia del aire la esfera cae mas rapido.

  
#include <GL/glut.h>
#include <stdlib.h>
#include <stdio.h>
#include <math.h>

#define	MAXPUNTOS	100
#define PI	3.1415926
#define g	9.81
#define coef_viscosidad	17.6e-6


double t[MAXPUNTOS+1], u1[MAXPUNTOS+1], u2[MAXPUNTOS+1];
double masa_fluido, masa_cuerpo, coef_friccion;

void init_parametros(void)
{
 double radio_cuerpo;
 double densidad_fluido;
 double densidad_cuerpo;

 radio_cuerpo=0.15;
 densidad_fluido=1.293;
 densidad_cuerpo=5.536;
 masa_fluido=(4.0/3.0)*PI*pow(radio_cuerpo, 3.0)*densidad_fluido;
 masa_cuerpo=(4.0/3.0)*PI*pow(radio_cuerpo, 3.0)*densidad_cuerpo;
 coef_friccion=6.0*PI*radio_cuerpo;
}


double f1(double t, double u1, double u2)
{
 return (u2);
}

double f2(double t, double u1, double u2)
{
 return (g*(1.0-(masa_fluido/masa_cuerpo))-coef_friccion*coef_viscosidad*u2);
}

double trayectoria_vacio(double t)
{
 return ((1.0/2.0)*g*pow(t, 2.0));
}

void RK4(double tinicial, double tfinal, 
		 double u1_inicial, double u2_inicial,
		 int n)
{
 double k1, k2, k3, k4;
 double l1, l2, l3, l4;
 double h;
 int i;

 h=(tfinal-tinicial)/n;
 t[0]=tinicial;
 u1[0]=u1_inicial;
 u2[0]=u2_inicial;
 for (i=0; i<n; i++)
	{
	k1=h*f1(t[i], u1[i], u2[i]);
	l1=h*f2(t[i], u1[i], u2[i]);
	k2=h*f1(t[i]+h/2.0, u1[i]+k1/2.0, u2[i]+l1/2.0);
	l2=h*f2(t[i]+h/2.0, u1[i]+k1/2.0, u2[i]+l1/2.0);
	k3=h*f1(t[i]+h/2.0, u1[i]+k2/2.0, u2[i]+l2/2.0);
	l3=h*f2(t[i]+h/2.0, u1[i]+k2/2.0, u2[i]+l2/2.0);
	k4=h*f1(t[i]+h, u1[i]+k3, u2[i]+l3);
	l4=h*f2(t[i]+h, u1[i]+k3, u2[i]+l3);
	u1[i+1]=u1[i]+(1.0/6.0)*(k1 + 2.0*k2 + 2.0*k3+ k4);
	u2[i+1]=u2[i]+(1.0/6.0)*(l1 + 2.0*l2 + 2.0*l3+ l4);
	t[i+1]=t[i] + h;
	}
}

void init(void)
{
 glClearColor(0, 0, 0, 0);
 glEnable(GL_LINE_SMOOTH);
 glEnable(GL_BLEND);
 glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
 glHint(GL_LINE_SMOOTH, GL_NICEST);
 init_parametros();
 RK4(0.0, 1.0, 0.0, 0.0, MAXPUNTOS);
}

void display(void)
{
 int i;

 glClear(GL_COLOR_BUFFER_BIT);
 glMatrixMode( GL_MODELVIEW_MATRIX );
 glLoadIdentity();

 //ejes
 glColor3f(0.0, 0.5, 0.8);  
 glBegin(GL_LINES);
  glVertex2f(0.0, 0.0);
  glVertex2f(1.0, 0.0);
  glVertex2f(0.0, 0.0);
  glVertex2f(0.0, 5.0);
 glEnd();

 //grafica de la solucion numerica en verde
 glColor3f(0.0, 1.0, 0.0);  
 glBegin(GL_LINE_STRIP);
 for (i=0; i<MAXPUNTOS; i++)
 	 glVertex2f(t[i], u1[i]);
 glEnd();

 //grafica de la trayectoria en el vacio en rojo
 glColor3f(1.0, 0.0, 0.0);  
 glBegin(GL_LINE_STRIP);
 for (i=0; i<MAXPUNTOS; i++)
 	 glVertex2f(t[i], trayectoria_vacio(t[i]));
 glEnd();

 glFlush ();
}

void reshape (int w, int h)
{
 if (!h)
	return;
 glViewport(0, 0, w, h);
 glMatrixMode(GL_PROJECTION);
 glLoadIdentity();
 gluOrtho2D(-0.2, 1.2, -0.2, 5.2);
 glMatrixMode(GL_MODELVIEW);
 glLoadIdentity();
}

void keyboard(unsigned char key, int x, int y)
{
 switch (key) 
   {
   case 27: exit(0);
             break;
   }
}    

int main(int argc, char** argv)
{
 glutInit(&argc, argv);
 glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
 glutInitWindowSize (350, 350); 
 glutInitWindowPosition (0, 0);
 glutCreateWindow ("Friccion en un Fluido");
 init ();
 glutDisplayFunc(display); 
 glutReshapeFunc(reshape);
 glutKeyboardFunc(keyboard);
 glutMainLoop();
 return 0;
}

valcoey@hotmail.com

Ramiro Alcocer, 2001