Principal | Gráficos 3D | Gráficos 2D | Fractales | Math | Códigos | Tutoriales | Links
Una superficie 3D, es la representación gráfica de una función
matematica de dos variables x, y,
la función f(x,y) tiene que ser continua, ejemplo:
f(x,y) = sin(PI*x) + sin(PI*y)
donde PI=3.14159..., los valores para x,y
estan en el intervalo [-Pi, Pi].
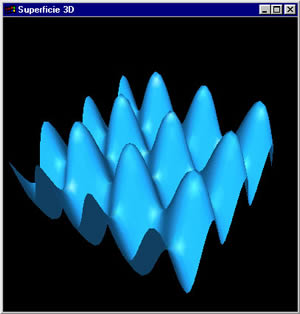
En el código fuente utilizo las rutinas de trackball
para rotar el grafico utilizando el mouse.
Codigo Fuente, Ejecutable : mesh.zip
/*
Graficacion de una funcion 3D, manteniendo presionado el boton
central del mouse y arrastrando se puede rotar el grafico en
cualquier direccion.
presionando "w" se obtiene una vista en modo wireframe (solo lineas)
presionando "f" se visualiza en el modo smooth.
Author : Ramiro Alcocer
Website : www.oocities.org/valcoey/index.html
Email : valcoey@hotmail.com
*/
#include <GL/glut.h>
#include <stdlib.h>
#include <math.h>
#include "trackball.h"
#define n_segs 40
#define max_puntos n_segs*n_segs
#define max_poligonos (n_segs-1)*(n_segs-1)
#define PI 3.141592654
struct {
GLfloat fVert1[3];
GLfloat fVert2[3];
GLfloat fVert3[3];
GLfloat fVert4[3];
GLfloat fNormal[3];
} Tri[max_poligonos];
GLfloat vertice[max_puntos][3];
GLfloat vnorms[max_puntos][3];
int poligonos[max_poligonos][4];
int numpoligonos;
int numvertices;
GLuint mesh_list = 0;
//defino el color y la posicion de la fuente de luz
GLfloat light_ambient[] = { 0.75f, 0.75f, 0.75f, 1.0f };
GLfloat light_diffuse[] = { 1.0f, 1.0f, 1.0f, 1.0f };
GLfloat light_position[] = { 0.0f, 0.0f, 1.0f, 0.0f };
GLfloat mat_ambient[] = {0.05f, 0.25f, 0.4f, 1.0f};
GLfloat mat_diffuse[] = {0.1f, 0.6f, 0.9f, 1.0f};
GLfloat mat_specular[] = {1.0f, 1.0f, 1.0f, 1.0f};
// trackball
GLuint trackball_lasttime;
GLfloat trackball_lastposition[3];
GLfloat trackball_angle = 0;
GLfloat trackball_axis[3];
GLboolean trackball_animate = GL_FALSE;
GLfloat trackball_transform[4][4];
//Calcula el modulo de un vector
GLfloat Modulo(GLfloat x, GLfloat y, GLfloat z)
{
GLfloat len;
len = x*x + y*y + z*z;
return ( sqrt(len));
}
//Normaliza el vector a mudulo 1
GLvoid Normaliza(GLfloat *x, GLfloat *y, GLfloat *z)
{
GLfloat len;
len = Modulo(*x, *y, *z);
len = 1.0/len;
(*x) *= len;
(*y) *= len;
(*z) *= len;
}
//Calcula el vector Normal
GLvoid CalculateVectorNormal(GLfloat fVert1[], GLfloat fVert2[],
GLfloat fVert3[], GLfloat *fNormalX,
GLfloat *fNormalY, GLfloat *fNormalZ)
{
GLfloat Qx, Qy, Qz, Px, Py, Pz;
Qx = fVert2[0]-fVert1[0];
Qy = fVert2[1]-fVert1[1];
Qz = fVert2[2]-fVert1[2];
Px = fVert3[0]-fVert1[0];
Py = fVert3[1]-fVert1[1];
Pz = fVert3[2]-fVert1[2];
*fNormalX = Py*Qz - Pz*Qy;
*fNormalY = Pz*Qx - Px*Qz;
*fNormalZ = Px*Qy - Py*Qx;
}
//funcion a graficar
float funcion3D(float x, float y)
{
return (sin(PI*x)+sin(PI*y));
}
void EvaluarFuncion(void)
{
GLfloat xdelta, ydelta;
GLfloat x, y;
float xmin, xmax;
float ymin, ymax;
int i, j, k;
xmin = -PI; xmax = PI;
ymin = -PI; ymax = PI;
xdelta=(xmax-xmin)/(n_segs-1);
ydelta=(ymax-ymin)/(n_segs-1);
x=xmin;
k=0;
for (i=0; i<n_segs; i++)
{
y=ymin;
for (j=0; j<n_segs; j++)
{
vertice[k][0]=x;
vertice[k][1]=y;
vertice[k][2]=funcion3D(x, y);
k+=1;
y+=ydelta;
};
x+=xdelta;
};
numvertices=k;
}
void GenerarMalla(void)
{
int i, j, h, k;
h=0; k=0;
for (i=0; i<(n_segs-1); i++)
{
for (j=0; j<(n_segs-1); j++)
{
poligonos[k][0]=h;
poligonos[k][1]=h+1;
poligonos[k][2]=h+n_segs+1;
poligonos[k][3]=h+n_segs;
h+=1;
k+=1;
};
h+=1;
};
numpoligonos=k;
}
void GenerarNormales(void)
{
GLfloat fNormalX, fNormalY, fNormalZ;
GLfloat sumx=0.0, sumy=0.0, sumz=0.0;
int i,j;
int shared=0;
for (j=0; j<numpoligonos; j++)
{
//Vertice 1
i=poligonos[j][0];
Tri[j].fVert1[0] = vertice[i][0];
Tri[j].fVert1[1] = vertice[i][1];
Tri[j].fVert1[2] = vertice[i][2];
//Verice 2
i=poligonos[j][1];
Tri[j].fVert2[0] = vertice[i][0];
Tri[j].fVert2[1] = vertice[i][1];
Tri[j].fVert2[2] = vertice[i][2];
//Vertice 3
i=poligonos[j][2];
Tri[j].fVert3[0] = vertice[i][0];
Tri[j].fVert3[1] = vertice[i][1];
Tri[j].fVert3[2] = vertice[i][2];
//Vertice 4
i=poligonos[j][3];
Tri[j].fVert4[0] = vertice[i][0];
Tri[j].fVert4[1] = vertice[i][1];
Tri[j].fVert4[2] = vertice[i][2];
//Calcula el vector normal al poligono
CalculateVectorNormal(Tri[j].fVert1, Tri[j].fVert2, Tri[j].fVert3,
&fNormalX, &fNormalY, &fNormalZ);
//nos retorna el vector unitario, es decir de modulo 1
Normaliza(&fNormalX, &fNormalY, &fNormalZ);
//almacena los vectores normales, para cada poligono
Tri[j].fNormal[0] = fNormalX;
Tri[j].fNormal[1] = fNormalY;
Tri[j].fNormal[2] = fNormalZ;
};
for (i=0; i<numvertices; i++)
{
for (j=0; j<numpoligonos; j++)
{
if (poligonos[j][0]==i || poligonos[j][1]==i ||
poligonos[j][2]==i || poligonos[j][3]==i)
{
sumx = sumx + Tri[j].fNormal[0];
sumy = sumy + Tri[j].fNormal[1];
sumz = sumz + Tri[j].fNormal[2];
shared ++;
}
}
vnorms[i][0] = sumx / (float) shared;
vnorms[i][1] = sumy / (float) shared;
vnorms[i][2] = sumz / (float) shared;
Normaliza(&vnorms[i][0], &vnorms[i][1], &vnorms[i][2]);
sumx=0.0;
sumy=0.0;
sumz=0.0;
shared=0.0;
}
}
void meshlist(void)
{
int i,j;
mesh_list = glGenLists(1);
glNewList(mesh_list, GL_COMPILE);
glBegin(GL_QUADS);
for (i=0; i<numpoligonos; i++)
{
j=poligonos[i][0];
glNormal3fv(vnorms[j]);
glVertex3fv(Tri[i].fVert1);
j=poligonos[i][1];
glNormal3fv(vnorms[j]);
glVertex3fv(Tri[i].fVert2);
j=poligonos[i][2];
glNormal3fv(vnorms[j]);
glVertex3fv(Tri[i].fVert3);
j=poligonos[i][3];
glNormal3fv(vnorms[j]);
glVertex3fv(Tri[i].fVert4);
};
glEnd();
glEndList();
}
void init(void)
{
glLightfv(GL_LIGHT0, GL_AMBIENT, light_ambient);
glLightfv(GL_LIGHT0, GL_DIFFUSE, light_diffuse);
glLightfv(GL_LIGHT0, GL_POSITION, light_position);
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glMaterialfv (GL_FRONT, GL_AMBIENT, mat_ambient);
glMaterialfv (GL_FRONT, GL_DIFFUSE, mat_diffuse);
glMaterialfv (GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialf (GL_FRONT, GL_SHININESS, 60.0f);
glEnable(GL_DEPTH_TEST);
glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);
EvaluarFuncion();
GenerarMalla();
GenerarNormales();
meshlist();
/* put the identity in the trackball transform. */
glPushMatrix();
glLoadIdentity();
glGetFloatv(GL_MODELVIEW_MATRIX, (GLfloat *)trackball_transform);
glPopMatrix();
tbInit(GLUT_MIDDLE_BUTTON);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glPushMatrix();
tbMatrix();
glCallList(mesh_list);
glPopMatrix();
glFlush();
glutSwapBuffers();
}
void reshape (int w, int h)
{
if (!h)
return;
tbReshape(w, h);
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(45, (GLfloat) w/(GLfloat) h, 1.0, 100.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.0, 0.0, -12.0);
}
void keyboard(unsigned char key, int x, int y)
{
switch (key)
{
case 'f':glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);
glutPostRedisplay();
break;
case 'w':glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
glutPostRedisplay();
break;
case 27: exit(0);
break;
}
}
void mouse(int button, int state, int x, int y)
{
tbMouse(button, state, x, y);
glutPostRedisplay();
}
void motion(int x, int y)
{
tbMotion(x, y);
glutPostRedisplay();
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode (GLUT_DOUBLE | GLUT_RGB);
glutInitWindowSize (400, 400);
glutInitWindowPosition (0, 0);
glutCreateWindow ("Superficie 3D");
init ();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutMouseFunc(mouse);
glutMotionFunc(motion);
glutMainLoop();
return 0;
}
|
Principal | Gráficos 3D | Gráficos 2D | Fractales | Math | Códigos | Tutoriales | Links