Chapter 8 Discussion and Future Research
The main approach in this research is straightforward maximum
likelihood method. This ensures sound theoretical foundation and makes
abundant MLE results readily applicable. It also makes easy to fully
utilize all information available in the data and to uniformly handle
complete, missing or censored data. In fact, data could be in the form
of any subset of sample space.
By integration over the observed range for incomplete measures, it is able to handle dataset with extremely heavy proportion of incomplete observations, as long as the integration is well defined and the maximum of the likelihood function exists. An extreme case is that when everything is missing, then the likelihood function is constant 1, so any parameter estimation is as good as others, or basically no solution exists in this case.
With the likelihood approach, it provides a framework to systematically handle different distributions once they are given. By using the Jacobian matrices to link different parameter representations, in a very consistent fashion it can deal with various parameter structures such as variance-covariance structure, mean-dispersion structure, etc. This approach so far covers all models in Proc Mixed of current SAS system version 8.0, with extension being able to analyze incomplete data.
Since the likelihood function is usually very complicated, how to maximize this function becomes crucial to the research. Therefore the EM algorithm is employed for this purpose and implemented by Monte Carlo Markov Chains (MCMC) via an augmented Gibbs sampler as given in Theorem 6.3. This Gibbs sampler is the key to make the whole approach practical. It is very efficient and easy to implement. It is able to sample from very complex distributions and in very large scale. The sampling essentially consists of a series of drawing from univariate uniform distributions, and sampling from truncated distributions requires no extra effort. The utilization of latent variables greatly simplifies the sampler. This tactic is ideal for sampling incomplete data in MCEM algorithms. In spirit of this augmented Gibbs sampler, the methodology in our approach can be easily extended to a much broader class of models to handle incomplete data.
8.1 Calculation of Complex Integrals
So far the approach is fully parametric on marginal likelihood function, where proper expectations are taken over those incomplete measures conditional on the observed information. The likelihood function could be extremely complicated. Due to the complexity of incompleteness in the dataset, the dimension of integration could be multiples of sample size, which could be very large. The calculation of such integrals or conditional expectations is central to this research. Since an explicit solution is rarely available, an iterative numerical method such as MCEM algorithm must be employed.
As pointed out by Zwillinger (1992), Monte Carlo techniques may be the only techniques that will obtain an estimate in a reasonable amount of computer time for multi-dimensional integrals. The classical Monte Carlo sample-mean method converges with order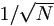 
, where N is the sample size, independent of dimension. The Quasi-Monte Carlo method can achieve much quicker convergence with an order of 
, where s is the dimension (Fang & Wang, 1994). If the integrand is smooth enough, s can be halved. Even so, a 6 dimensional integral will need about O(1012) trials to achieve an accuracy of 10-8.
As to maximizing the likelihood function, under suitable distributional assumptions, the calculation could be simplified significantly with specific techniques, for instance, the augmented Gibbs sampler developed in Theorem 6.3 is very efficient and particularly suitable for sampling from truncated distributions and EM style algorithms. It could be easily extended to exponential family and many other distributions. It also has the ability to draw very large samples, as it has been a major technique in the image-processing and other large scale models.
In the past, the complexity in calculating these multi-dimensional integrals was prohibitive for exploiting such full likelihood approach. As computing power has been improving dramatically in recent years, these integral calculations are no longer as overwhelming as it was. As demonstrated by the simulations and real data analyses in Chapter 7, such calculations now become more and more affordable with proper techniques. We believe that computing intensive methods, especially those based on Monte Carlo Markov Chains (MCMC), should play more important roles in today and future statistical analyses for better using all data information.
We have generalized a broad class of models from handling only complete data to being able to handle incomplete data as well. In Chapter 3, we outlined the general framework of the method for incomplete data without specifying any model. Since it is independent of model and distributional assumptions, Chapter 3 could serve as foundations for a systematic approach to models with incomplete data for future research.
Although the approach is generally applicable to a very broad class of models, computation involved in the application to any specific model is not straightforward. With more assumptions given, more detailed method will be developed. Theorem 3.1 showed the general EM algorithm for models from exponential family. In Chapter 4, we have derived in details about EM algorithm for incomplete data in Mixed Models from exponential family distributions (Theorem 4.1), especially those with multivariate normal distribution (Theorem 4.4).
Chapter 4 also illustrates how to use the general framework outlined in Chapter 3. Follow the similar path, it is expected that we can obtain more detailed results for Generalized Linear Models (GLM), Hierarchical Generalized Linear Models (HGLM) (Lee & Nelder, 1996) and many others models with incomplete data from exponential families or more general distributions. To develop more detailed theory for other conventional methods is a natural continuation of this work.
In general, there should have no difficulty in developing a similar augmented Gibbs sampler as given in Theorem 6.3 for these more advanced models under more general distributions. This should makes the E-step very easy with Monte Carlo simulation, while the M-step could be solved by nonlinear numerical methods.
All our approaches are parametric with certain distributional assumptions. However, non-parametric approach as in Buckley-James estimator (Buckley & James, 1979) would be also important. It could be a relevant future research direction.
Although non-parametric approach is usually complicated, it is always appealing as without worrying about the validity of distribution assumptions. The framework outlined in Chapter 3 would be useful even in this setting. The technique used in Buckley-James estimator is essentially a non-parametric version of the EM algorithm.
Section 1.5.2 gave some review about the extensions of Buckley-James method to handle censored multivariate data in AFT models. Two such approaches are the marginal independence approach (Lee et al., 1993) and linear mixed effect model approach (Pan & Louis, 2000). The latter is essentially a semi-parametric approach.
One interesting observation given by Heller and Simonoff (1990) is that, with censored data, the Buckley-James estimator is even better than MLE, provided we have a parametric model with correct distribution and then obtain MLE. As they explained, one
possible reason is that Buckley-James estimator estimates
using an estimate of the entire residual
distribution, while MLE does so with only few parameters, which is not
enough in this case. This suggests that non-parametric or
semi-parametric approach would probably have some advantages.
Another relevant observation is that, the usual normal random-effect assumption may not influence the asymptotic validity of the model. Verbeke and Lesaffre (1997) have shown that for the mixed model with complete data, the maximum likelihood estimates of the regression coefficient and the variance component of the error term obtained under normality assumptions for both the random effect and the error term are consistent and asymptotically normal, even though the true distribution of the random effect is not normal. In fact, the marginal likelihood score equations based on normality assumptions for both the random effect and the error distribution are normal equations, a special case of GEE (Liang & Zeger, 1986). By the general theory of GEE, the resulting estimates of the regression coefficients are consistent and asymptotically normal, even when neither the random effect nor the random error term has a normal distribution. For finite samples, Butler and Louis (1992) have shown that misspecified random-effect distribution has little effect on the fixed effect estimates. However, further study is needed for censored data.
8.4 Data Analysis and Data Incompleteness
The simulation in Chapter 7 shows that this approach could work with extremely severe censoring or missing, as it seems that even 80%-90% might be still ok under certain models. Then an interesting research direction is to study the relationship between algorithm convergence and data incompleteness. (1). How much incomplete data is too much? (2). When the algorithm will not converge at all? In general, the more incomplete data, the slower the convergence. Wider censoring ranges also make the convergence slower. Besides these simple observations, further research could be interesting and important.
A closely related question is how to account for the incomplete observation in determining the effective sample size. It has significant effect on how to apply the asymptotic properties of MLEs derived under large sample assumption. Clearly, the sample size depends not only on the number of subjects, but also on how much information each observation provides. As shown by simulations, when censoring range widens (i.e. information in the observation decreases), the estimation of standard error for MLE gets larger.
Another interesting observation is from the analyses of the motivating data in Chapter 7. In conventional analysis, when outcome variable y is missing, we basically have to discard it. However, in the MCEM approach, we intentionally incorporate some “extra” information as we know that y is in fact always positive. On the other hand, this kind of information cannot be easily integrated into conventional analysis such as linear mixed model. Generally such information is trivial, but sometimes it is not. Besides y is always positive, we may also have other additional information for incomplete data, for example, rank information such as y1 < y2, or the variable distribution over its incomplete range. Apparently, these kinds of information could be easily incorporated into our approach. Ranking or other constraining conditions merely define certain integration ranges, which could be taken into account in the Gibbs sampler. In the case of known distribution, for instance, via such knowledge on the biology of the biomarker as low dose response curve and distribution, the likelihood function and the Gibbs sampler can be easily modified accordingly as well. To sum up, our approach is much easier to utilize such information that is true but cannot be used in conventional methods. This kind of information usually cannot be expressed by an exact number, but instead by a range, a relationship, a curve, and so on that is hard to quantify in conventional sense.