0102 Колмогоровын магадлалыг тооцоолох
аксиом
Аксиом 1. (сєрєг утга байх ёсгvй)
Р(А)  0 нь бvх vзэгдэл А д хvчинтэй.
0 нь бvх vзэгдэл А д хvчинтэй.
Аксиом 2. (нормчилохуй)
Р( )
= 1
)
= 1
Аксиом 3. (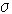 гийн нэмэгдэх, нийлбэрийн чадвар)
гийн нэмэгдэх, нийлбэрийн чадвар)
А1, А2,.... ууд нь зарим талаар
салаална. 

Р бол S 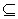 Pot
(
Pot
( )
гэсэн vзэгдлvvдийн системийн тодорхойлох мужид орших функц юм.
)
гэсэн vзэгдлvvдийн системийн тодорхойлох мужид орших функц юм.
S нь нь A 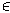 S гэсэн vзэгдэл бvрт
S гэсэн vзэгдэл бvрт  гэсэн давхар vзэгдлийг агуулах ба эднийх нь дундаж болон нийлмэл
нь тоолж болохуйц мєн тєгсгєлгvй байвал S ийг
гэсэн давхар vзэгдлийг агуулах ба эднийх нь дундаж болон нийлмэл
нь тоолж болохуйц мєн тєгсгєлгvй байвал S ийг  дэхь
дэхь 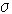 Algebra
гэнэ.
Algebra
гэнэ.
P : S 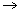
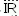 нь 1,2,3 дугаар аксиомуудыг батлах бєгєєд энэ тохиолдолд Р ийг
Магадлалын нийт хэмжээ гэж vзнэ. Мєн (
нь 1,2,3 дугаар аксиомуудыг батлах бєгєєд энэ тохиолдолд Р ийг
Магадлалын нийт хэмжээ гэж vзнэ. Мєн ( ,
S, P) хэмээх гурвалыг магадлалын орон зай гэнэ.
,
S, P) хэмээх гурвалыг магадлалын орон зай гэнэ.
Магадлалын алгебр буюу магадлалыг тооцоолох бvх vйлдэл нь Аксиомуудаас
урган гардаг.
Дvрэм. S ээс бий болох дурын А vзэгдлийн
хувьд P( )
= 1-P(A)
)
= 1-P(A)
А1, А2,...Am гэсэн
тєгсгєлєг тоо хэмжээ эсвэл  ийн А1, А2,..... гэсэн цувааг
ийн А1, А2,..... гэсэн цувааг
 болон
болон
 гэсэн нєхцлийг хангаж байвал
гэсэн нєхцлийг хангаж байвал  ийн задаргаа гэнэ.
ийн задаргаа гэнэ.
Дvрэм. Аi нь  ийн задаргаа бол дараахи нь хvчинтэй.
ийн задаргаа бол дараахи нь хvчинтэй.

харин В vзэгдэл бvрийн хувьд

нь хvчинтэй.
Дvрэм. P(A B)
= P(A) + P(B) - P(A
B)
= P(A) + P(B) - P(A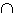 B)
B)
жишээ. (шоо хаях)
A = {w2,w4,w6}, B = {w1,w2,w3}
5 байхгvй байгааг анзаарна уу.
A B
= {w1,w2,w3,w4,w6}
B
= {w1,w2,w3,w4,w6}
P(A) = P(B) = 1/2, P(A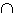 B)
= ({w2}) = 1/6
B)
= ({w2}) = 1/6
P(A B)
= 1/2 + 1/2 - 1/6 = 5/6
B)
= 1/2 + 1/2 - 1/6 = 5/6

