02 Хувьсах хэмжигдэхvvнvvд

Нэг хэмжээст хувьсагч хэмжигдэхvvнvvд болон тархалтын функц.

гэсэн нийт vзэгдлийн хэмжээ бvхий туршилт єгєгдсєн байг. Эдгээр vр дvнг тодорхой тоогоор илэрхийлэх хэрэг гарна : w

гэсэн нийт хэмжилтvvд гарч ирэх бєгєєд бидэнд бvгдээрээ биш зєвхєн хэмжилтийн тодорхой Утгууд нь хэрэг болдог.

Дvрсэлж vзvvлэх юм бол энэ функц нь

х 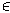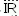ийн хувьд тодорхойлж болох бvх магадлал нь

хувьсах хэмжигдэхvvн болох Х ийн хувьд vзэгдлийн тоо хэмжээ.

Жишээ: шоо.

жишээ: биеийн єндєр.

Тодорхойлолт. Магадлалын орон зай єгєгдсєн байг. (,S, P)

хэрэв хангагдаж байвал

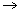
Х : 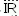функцийг хэмжиж болохуйц гэж vзээд Хувьсах хэмжигдэхvvн гэнэ.

Тодорхойлолт. F :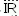 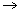[0,1] гэсэн функц :

гэсэн шинжийг агуулж байвал

F - нь монотон маягаар байнга єсєхгvй.

F нь тасралтгvй

Тархалтын Функц гэнэ.

Бvх Х хувьсах хэмжигдэхvvнvvд нь

гэсэн тархалтын функцээр тодорхойлогддог.

F_X нь Х ийн тархалтын функц гэж нэрлэгддэг.

Жишээ. Х нь шоо хаях vед гарах нvдний тоо гэж vзье.

P(X=i) = 1/6          i=1,...,6

болон

гэдгээ F нь 1/6 гэсэн хэсгээр 1,2,3,4,5,6 дугаар байранд тус бvр байрлах шаталсан функцийг vvсгэж байна.

жишээ. хэрэв тасралтгvй функц байх юм бол,

нь Х хувьсагч хэмжигдэхvvний тархалтын функц бол дараахи нь хvчинтэй.

Хэрвээ аль нэг тархалтын функцийн х 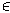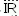ийн бух утга дорхи магадлалд тохирч байвал

vvнээс илvv нарийн vзэгдлийн магадлалыг олж болдог.

Жишээ. Нэмэгдэх буюу нийлбэрийн чанараас а < b буюу

ийг бvх хэрэглээнд тохирох хvрэлцэхvйц их хэмжээний vзэгдлийн систем гэж vзвэл

P(X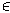B) гэсэн магадлал нь бvх ийн хувьд тохирох ёстой.

Тодорхойлолт. хамгийн бага нь доторхи бvх интервалийг агуулж байвал Борелийн 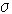-Algebra гэдэг.

ийн бvх элэментvvдийг Борелийн хэмжээ гэдэг.

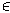
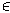Бvх В ийн хувьд Р(ХВ) гэсэн нийт магадлал нь Х ийн магадлалын тархалт болно.

 

 

[ 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21]

ашигласан материал : TU-Dresden. Skript von Stat. I