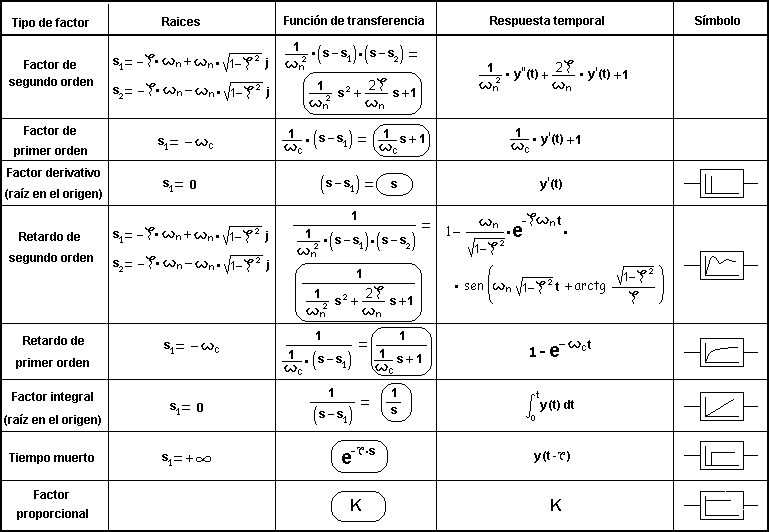

La siguiente figura contiene los diagramas de Bode de un sistema obtenidos experimentalmente. Se han dibujado las asíntotas en el diagrama del módulo sabiendo que sus pendientes son siempre múltiplo de 20 dB/dec o -20 dB/dec, ya que las gráficas no son exactamente rectas en los puntos con cambio de pendiente. Los puntos de corte de las asíntotas determinan las frecuencias de cruce de factores de primer orden (o retardos de primer orden) o las frecuencias naturales de factores de segundo orden (o retardos de segundo orden). Donde la pendiente aumenta en 20 dB/dec habrá un facor de primer orden y si disminuye en 20 dB/dec habrá un retardo de primer orden. Si el cambio de pendiente es de 40 dB/dec habrá factor de segundo orden si la pendiente se incrementa, o retardo de segundo orden si la pendiente disminuye. En la parte derecha de la figura se han resaltado en negrita los factores que se obtienen a partir de los diagramas y que se explican a continuación.
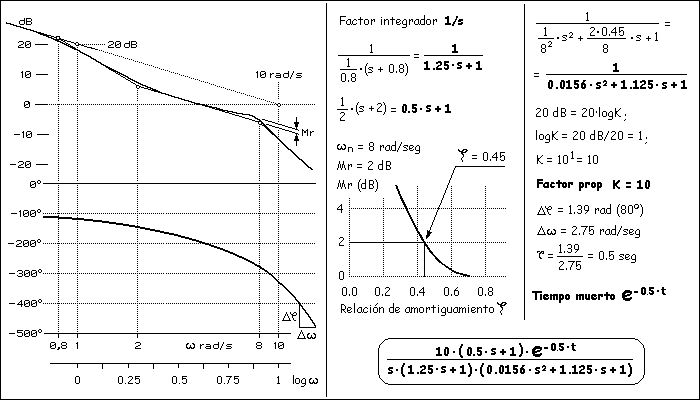
En la figura se comprueba fácilmente que la pendiente a las frecuencias más bajas (comenzando por la izquierda) es de -20 dB/dec, ya que entre las frecuencias de 1 y 10 radianes por segundo, que es una década, corresponde un incremento de módulo de 20 dB, lo que significa que existe un factor integrador, ya que los integradores tienen su frecuencia de cruce en 0 rad/seg y si existe se detectará una caida de 20 dB/dec a las frecuencias más bajas. A la frecuencia de 0.8 rad/seg la pendiente pasa a ser de -40 dB/dec, lo que supone una caida (respecto de la pendiente anterior) de 20 dB/dec, correspondiente a un retardo de primer orden con frecuencia de cruce de 0.8 rad/seg. Por tratarse de una caida de pendiente, el polinomio de su función de transferencia aparece en el denominador, es decir, es el inverso de un factor de primer orden. A la frecuencia de 2 rad/seg la pendiente pasa a ser de -20 dB/dec, lo que supone un aumento de 20 dB/dec correspondientes a un factor de primer orden con frecuencia de cruce de 2 rad/seg. Se puede observar que la gráfica no se ajusta exactamente a las asíntotas en los factores y en los retardos de primer orden. Concretamente, a la frecuencia de cruce existe una diferencia de 3 dB y a la mitad y al doble de la frecuencia de cruce existe una diferencia de 1 dB. Esta sencilla regla permite trazar la curva con buena exactitud si se conoce la función de transferencia y se quiere dibujar sus diagramas de Bode.
Siguiendo con el ejemplo, se observa que hay un último cambio de pendiente a la frecuencia de 8 rad/seg, pero esta vez existe una caida de 40 dB/dec, que se corresponde con un retardo de segundo orden. Trazando una paralela a la asíntota y midiendo el pico de resonancia (Mr) se puede determinar la relación de amortiguamiento de forma aproximada si se compara con la gráfica de la siguiente figura. En el ejemplo se ha considerado un pico de resonancia Mr = 2 dB, que al compararlo con el diagrama del módulo de la siguiente figura, se ajusta bastante a la gráfica con relación de amortiguamiento igual a 0.5. Se afina un poco más al consultar la gráfica de Mr en función de la relación de amortiguamiento (siguiente figura), resultando para un Mr = 2 una relación de amortiguamiento de 0.45. Una vez que se conoce la frecuencia natural (8 rad/seg) y la relación de amortiguamiento (0.45), se determina la función de transferencia del retardo de segundo orden.

Una vez que se han determinado todos los factores correspondientes a los cambios de pendiente, aún falta determinar el factor proporcional, es decir, la ganancia K del sistema. Puesto que los diagramas del módulo de los factores se suman, el módulo MdB = 20·logK a la frecuencia de 0 rad/seg permitirá calcular la ganancia K como: K = 10 elevado a MdB/20. Esto resulta sencillo con sistemas que no contienen integrador, ya que la primera asíntota, a bajas frecuencias, es horizontal. Pero en sistemas con uno o dos integradores (en la práctica no hay sistemas con más integradores) no se puede determinar el módulo a la frecuencia de 0 rad/seg, debido a la escala logarítmica de la frecuencia. Este inconveniente queda superado si se considera el módulo a la frecuencia de 1 rad/seg (en lugar de 0 rad/seg) y todos los factores, excepto el proporcional, se determinan "normalizados", tal como se ha hecho hasta el momento. De esta forma, los diagramas del módulo de cada factor tienen un módulo igual a 0 a la frecuencia de 1 rad/seg, tal como se consideró en el tema "Bloques en que se descompone un sistema".
Por consiguiente, el módulo MdB = 20·logK a la frecuencia de 1 rad/seg permite calcular la ganancia del sistema como: K = 10 elevado a MdB/20. Sin embargo, es posible que la primera asíntota no llegue a la frecuencia de 1 rad/seg, como es el caso que estamos resolviendo, ya que la primera frecuencia de cruce (0.8 rad/seg) es menor de 1. En estos casos se resuelve simplemente prolongando la asíntota hasta la frecuencia de 1 rad/seg. Así se ha determinado el factor proporcional viendo que el módulo con 1 rad/seg es igual a 20 dB, de modo que saldrá una ganancia K = 10 elevado a 20/20 = 10 elevado a 1 = 10. De esto se deduce una forma inmediata de calcular la ganancia K si se prolonga la primera asíntota hasta cortar a la horizontal de 0 dB, ya que entonces la frecuencia en el punto de corte, en rad/seg, coincide con la ganancia K. En la figura con el ejemplo que estamos siguiendo se ha marcado el punto de corte, resultando 10 rad/seg, que, como se ha dicho, coincide con la ganancia K. Si el sistema tuviera dos integradores, la pendiente de la primera asíntota sería de -40 dB/dec y su prolongación hasta cortar la horizontal a 0 dB estará a una frecuencia que ya no coincidiría con la ganancia K sino con la raíz cuadrada de K.
Llegados a este punto, solo falta determinar si el sistema tiene retardo de transporte. Para ello nos valemos de los factores ya calculados, sumando sus fases teóricas a elevada frecuencia, es decir, su atraso o adelanto máximo de fase: Integrador (-90º) + retardo 1º orden (-90º) + factor 1º orden (+90º) + retardo de segundo orden (-180º) + factor proporcional (0º) = -270º. Este resultado no se parece en nada al retraso tan grande que vemos en la figura con los diagramas de Bode, por lo que deducimos que existe tiempo muerto. El tiempo muerto del sistema se puede calcular como la pendiente del diagrama de fase a frecuencias altas, entendiendo como altas frecuencias cuando sean significativamente mayores que las frecuencias de cruce que se ha determinado. Así ha resultado un tiempo muerto igual a 0.5 segundos, lo que completa la función de transferencia del sistema planteado. En cuanto a la pendiente del diagrama de fase a elevada frecuencia, se ha calculado considerando dos puntos próximos y haciendo el cociente entre los incrementos vertical y horizontal. Esta aproximación es más precisa si los puntos están muy próximos.
Sistemas con factores de primer orden en los que su raíz es positiva.
Hay que recordar esta posibilidad porque podríamos equivocarnos al interpretar alguno de los factores que determinan la función de transferencia. Si existe un factor de primer orden con raíz positiva, no puede detectarse por el diagrama del módulo obtenido experimentalmente, ya que será el mismo que si la raíz es negativa. Haciendo una estimación del ángulo de fase a una frecuencia elevada (comparado con las frecuencias de cruce), suponiendo raices negativas, entonces si existe un factor de primer orden con raíz positiva, resultará una fase 180º menor que la estimada, ya que se habría supuesto un adelanto de 90º para el factor de primer orden y la realidad será que tiene un atraso de 90º, siendo la diferencia 180º como se ha dicho.