筆者在《廣義量詞系列:古典推理模式》中介紹了「三段論推理」。可以
說,「三段論推理」在古典形式邏輯中佔有核心地位。在中古時期,「三段論推理」甚至幾乎成為「邏輯學」
的同義詞。可是,隨著現代數理邏輯的興起,「三段論推理」在邏輯學中的地位已大不如前。儘管在今天有關
「三段論推理」的知識仍會在形式邏輯的課程或教科書中被傳授,但它在今天只是作為一種「古典」知識被保
存著,而不再成為數學或科學推理的指導原則。
不過,近年來「三段論推理」又重新引起某些學者的研究興趣,並且獲得新的發展。Peterson在
Intermediate Quantifiers – Logic, linguistics, and Aristotelian semantics一書中便以大量篇幅
討論把傳統的「三段論推理」推廣至「中間量詞」的問題,並提出一些新的推理格式和推理規則。模糊數學的
創立人Zadeh在A Computational Approach to Fuzzy Quantifiers in Natural Languages一文中則用
模糊數學的方法把「三段論推理」推廣至「模糊量詞」。受上述學者思想的啟發,筆者認為我們還可以把「三
段論推理」推廣至更廣闊的層面,例如「疑問量詞」和表達空間關係的詞項。本文將介紹上述學者的理論成果
,並加上筆者個人對這個課題的一些粗淺體會和嘗試。筆者希望透過本文的討論向讀者展示,儘管「三段論推
理」是一門古老的學科,但只要我們把它與適當的現代數學/邏輯學/語義學理論加以結合,便可以為它注入
新的內容和活力。
如前所述,Peterson把「三段論推理」推廣至「中間量詞」(即「全稱量詞」"all"和「存在量詞」 "some"以外的量詞)。在其著作中,Peterson分三個階段進行這種擴充。首先,他把「三段論推理」推 廣至三個常用的「中間量詞」:"(almost all)" (等同於"(few ... not)")、"most"和 "many"。接著,他把「三段論推理」推廣至「分數量詞」(例如"(more than 2/3)")以至「複雜 分數量詞」(例如"(much more than 2/3)")。最後,他把「三段論推理」推廣至「關係命題」,即主語 和賓語均帶有量詞(亦即「廣義量詞理論」所稱的「迭代量詞」)的命題。以下筆者將集中介紹包含上述三個「 中間量詞」以及「分數量詞」的「三段論推理」。
Peterson大大擴充了「三段論推理」有效推理格式的數目。傳統「三段論推理」共有24種有效格式(詳見 《廣義量詞系列:古典推理模式》),經上述第一階段擴充後,有效推理格 式便增至93個。舉例說,「ABB-2式」便是其中一個新的有效推理格式(註1),以下是這個格式的一個實例:
| 大前提: | 所有嘉賓都有邀請卡。 |
| 小前提: | 幾乎所有學生都沒有邀請卡。 |
| 結論: | 幾乎所有學生都不是嘉賓。 |
經第二階段擴充後,有效推理格式的數目便更多。但由於「分數」(即數學上的「有理數」)的數目無限,我們 無法一一為各個含有「分數量詞」的語句命名,因而也無法列舉全部有效格式。因此,Peterson只能舉出一些 含有「分數量詞」的有效推理格式的例子,例如:
| 大前提: | (more than 1/8)(M)(~P) | |
| 小前提: | (at least 7/8)(M)(S) | (1) |
| 結論: | some(S)(~P) |
以下是上述格式的一個實例:
| 大前提: | 在八名學生中,有多於一人不穿校服。 |
| 小前提: | 在八名學生中,至少七人戴眼鏡。 |
| 結論: | 有戴眼鏡者不穿校服。 |
Peterson不僅提出新的「三段論推理」格式,還嘗試證明這些格式的有效性。Peterson使用至少兩種方法來證 明新的推理格式,第一種方法主要針對"(almost all)"等三個「中間量詞」,這種方法要用到「對當關 係推理」以及「命題邏輯」中的某些定理和證明技巧。舉例說,設我們要證明前述有效的「ABB-2式」,即以下 推理形式:
| 大前提: | all(P)(M) |
| 小前提: | (almost all)(S)(~M) |
| 結論: | (almost all)(S)(~P) |
我們首先利用「命題邏輯」中的下述定理(註2):
即我們把上述推理形式作如下變換:以原「結論」的否定來作為新「小前提」(「大前提」保持不變),並嘗試 推出原「小前提」的否定作為新「結論」。由於根據《廣義量詞系列:直接推 理的革新》中的「五層對當方陣」,句B的否定是句K,所以我們最終把上述推理形式變換為:
| 大前提: | all(P)(M) |
| 小前提: | many(S)(P) |
| 結論: | many(S)(M) |
請注意上述推理形式已從原來的「ABB-2式」變為「AKK-1式」。接下來的任務就是證明「AKK-1式」是有效的,
這不難證明,因為如果所有P是M,並且很多S是P,那麼這些是P的S自然也是M,所以我們最終可得出結論:很多
S是M。
Peterson使用的第二種證明方法主要針對「分數量詞」,這種方法要用到簡單的代數運算和「反證法」。設我
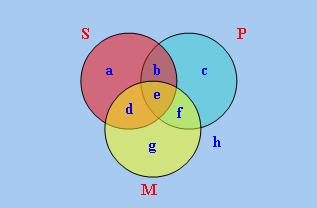
們要證明上面(1)的有效性,為方便證明,我們參照以下「溫氏圖」以字母標示S、P、M及其否定的各種交集的
基數(請注意在下圖中,由於a ... h等代表集合基數,我們有a ≥ 0 ... h ≥ 0):

以下我們用「反證法」證明(1)。為此,我們須先使用「廣義量詞理論」對量詞的定義(詳見 《廣義量詞系列:基本單式量詞》的表3)並參照上圖中的區域把(1)中的兩 個前提和結論的否定轉化為代數式。舉例說,由於(1)的大前提「(more than 1/8)(M)(~P)」的集合論 定義為|M ∩ ~P| / |M| > 1/8,而|M ∩ ~P|和|M|分別相當於上圖中的d + g和d + e + f + g,該語句 應轉化為(d + g) / (d + e + f + g) > 1/8 (註3)。以下 是(1)的證明:
| (i) | (d + g) / (d + e + f + g) > 1/8 | 大前提 | |
| (ii) | (d + e) / (d + e + f + g) ≥ 7/8 | 小前提 | |
| (iii) | a + d = 0 | 結論的否定 | |
| (iv) | d = 0 | 從(iii)推出 | |
| (v) | 8(d + g) > (d + g) + (e + f) | 化簡(i) | |
| (vi) | 7(d + g) > e + f | 化簡(v) | |
| (vii) | 7g > e + f | 用(iv)化簡(vi) | |
| (viii) | 8(d + e) ≥ 7(d + e) + 7(f + g) | 化簡(ii) | |
| (ix) | d + e ≥ 7(f + g) | 化簡(viii) | |
| (x) | e ≥ 7f + 7g | 用(iv)化簡(ix) | |
| (xi) | 7f + 7g ≥ 7g | 數學常識 | |
| (xii) | e > e + f | 從(x)、(xi)和(vii)推出 |
上面第(xii)行就是我們要推出的矛盾,此一矛盾間接證明了(1)的有效性。
Peterson還嘗試把傳統的「三段論」推理規則推廣到更一般的情況。古典形式邏輯除了嘗試找出所有有效的「
三段論」推理格式外,還嘗試總結出一些推理規則,以便讓進行推理的人根據這些規則,便能直接推出某一推
理格式是否有效,而無須查考有效推理格式的清單。古典形式邏輯總結出六條推理規則和七種「謬誤」,這七
種「謬誤」都有專門的名稱,其中三種涉及到「周延性」的概念:「中詞不周延的謬誤」、「大詞不當周延的
謬誤」和「小詞不當周延的謬誤」,由此可見「周延性」概念對傳統「三段論推理」的重要性。
古典形式邏輯對「周延性」作如下界定:全稱命題中的主語以及否定命題中的謂語都是「周延」的,其他情況
下的主語和謂語都是「不周延」的。可是,古典形式邏輯並沒有論證「周延性」與推理規則的關係。換句話說
,「周延性」與推理規則的關係僅是傳統邏輯學家的一種經驗總結,傳統邏輯學家沒有為這種關係提供理據。
事實上,由於「周延性」概念缺乏理據,且難以與現代數理邏輯上的其他概念整合,現代數理邏輯完全拋棄了
此一概念。
Peterson沿用古典形式邏輯的「周延性」概念,並把它推廣為「周延度」(註4)。在古典形式邏輯中,「周延性
」是二值概念,只有「周延」和「不周延」這兩個值。Peterson則把它推廣為多值概念,他把「全稱肯定命題」
的主語以及所有否定命題的謂語的「周延度」定為1,並把「存在肯定命題」的主語以及所有肯定命題的謂語的
「周延度」定為0。換句話說,他以數字1和0代替傳統邏輯中的「周延」和「不周延」這兩個值。至於各種「中
間量詞」的「周延度」,則按其接近"all"的程度而被定為0與1之間的某個分數。舉例說,
"(almost all)"、"most"和"many"的「周延度」便分別被定為3/4、2/4和1/4;各種「
分數量詞」的「周延度」則被定為相應的分數,例如"(at least 1/8)"的「周延度」就是1/8。
Peterson在推廣「周延性」概念後,亦對傳統的「三段論」推理規則作出修改,使之適用於各種「中間量詞」
。
Peterson的工作無疑大大豐富了傳統「三段論推理」的內容,亦為此一歷史悠久的邏輯分支注入了新內容。不
過,Peterson的研究在幾方面仍有不足之處。首先,他對「三段論推理」的革新主要是在傳統的框架下進行的
,例如他仍以「周延度」作為推理規則的一個重要因素。如前所述,由於「周延度」概念缺乏理據,他所提出
的推理規則仍只具有經驗總結的性質(註5)。
其次,儘管Peterson引入了一些代數方法用來表達和證明某些涉及「分數量詞」的有效推理格式,但他沒有全
面採用「廣義量詞理論」的集合論定義,因此他所引入的新量詞只局限於"(almost all)"、
"most"、"many"、「分數量詞」和「複雜分數量詞」等,而未能包羅更多量詞。
最後,Peterson所提出的「中間量詞」其實混雜著「模糊量詞」與「非模糊量詞」,例如"(almost
all)"、"many"以及「複雜分數量詞」都是「模糊量詞」。可是,Peterson並沒有區別對待兩者,
他只是憑語感和初等代數而非模糊數學的方法處理這些量詞。舉例說,他只是憑語感把「many(S)(~P)
」當作「(almost all)(S)(P)」的矛盾命題,並以此構造他的「五層對當方陣」,然後進而以此作為證
明他所提出的新有效格式的依據。可是他對"many"的上述處理方法卻是有爭議的,因為"many"
這個詞帶有歧義,有時表達絕對數量,有時則表達相對數量,有時更兼有上述兩重意思,Peterson沒有作出清
楚說明,因此他所提出的涉及"many"的「三段論」推理格式便具有爭議性。在處理「複雜分數量詞」時
,Peterson採用代數學上的符號「>>」以表示"much more than"。但由於「>>」是模糊概念,難以應用於代數
運算,所以有時他又不得不利用以下關係作為「>>」的近似定義:
由於上述兩種處理「模糊量詞」的方法都有可爭議之處,這就使得Peterson提出的某些有效推理格式理據不足 。鑑於Peterson的方法有上述的不足之處,以下筆者將介紹循其他途徑推廣「三段論推理」的方法。
筆者認為,推廣「三段論推理」的其中一種有效方法是根據「廣義量詞理論」對四個傳統「量化句」的集合論
定義透徹分析「三段論」各有效格式的背後原理,然後把這些格式中的「全稱量詞」/「存在量詞」代之以其
他適當的量詞,從而得到新的有效格式。筆者認為這種方法最適合用於表示數值比較的量詞以及某些「例外結
構」,以下我們討論幾個例子。
我們首先以「IAI-4式」為例說明上述方法,以下是「IAI-4式」的形式:
| 大前提: | some(P)(M) |
| 小前提: | all(M)(S) |
| 結論: | some(S)(P) |
現在讓我們來探討這個有效格式背後的原理。根據「廣義量詞理論」的集合論定義,我們可以把上面的大前提 表達為P ∩ M ≠ Φ。但為方便以下討論,我們把此式改寫為|P ∩ M| > 0。同樣,我們把上面的 小前提表達為M ⊆ S。接著我們應用以下集合論定理(註6):
| 定理1: | 設A ⊆ B,則對任何集合C和實數n而言, | |
| (1) | |C ∩ A| >(≥) n ⇒ |C ∩ B| >(≥) n | |
| (2) | |C ∩ B| <(≤) n ⇒ |C ∩ A| <(≤) n | |
| (3) | |C ∩ A| ≤ |C ∩ B| | |
利用定理1(1)和「∩」運算的交換性,便容易得到|S ∩ P| > 0,而這正是上面的結論所要表達的意思 。請注意在上述討論中,實數0沒有任何特殊性,它可以為任何實數n取代,這等同於把上述有效格式中的量詞 "some"改為"(more than n)",這樣我們便得到一個有效的「數值三段論」格式:
| 大前提: | (more than n)(P)(M) |
| 小前提: | all(M)(S) |
| 結論: | (more than n)(S)(P) |
以下推理就是應用這個有效格式的實例:
| 大前提: | 多於十位得獎人戴襟花。 |
| 小前提: | 所有戴襟花的都坐在台上。 |
| 結論: | 多於十位坐在台上的是得獎人。 |
如能選擇恰當的格式和作出恰當的變換,我們也可以推導出包含量詞"(at most n)"的有效格式。舉例 說,我們可以選用「EAE-2式」,即:
| 大前提: | all(P)(~M) |
| 小前提: | all(S)(M) |
| 結論: | all(S)(~P) |
請注意上面的大前提「all(P)(~M)」等價於「no(P)(M)」。本來後一式一般可用集合論語言表 達為|P ∩ M| = 0,但為方便以下推導,我們把此式改寫為|P ∩ M| ≤ 0 (集合個數不可能為負數) 。同樣,我們把上面的小前提表達為S ⊆ M。接著,利用定理1(2),容易推得|S ∩ P| ≤ 0,這正 是上面的結論所要表達的意思。由於在上述討論中,0沒有任何特殊性,它可以為任何實數n取代,這實際等同 於把上述有效格式中的"no"改為"(at most n)",這樣我們便得到以下這個有效的「數值三段論 」格式:
| 大前提: | (at most n)(P)(M) |
| 小前提: | all(S)(M) |
| 結論: | (at most n)(S)(P) |
以下推理就是應用這個有效格式的實例:
| 大前提: | 最多十名學生穿運動服。 |
| 小前提: | 所有參賽者都穿運動服。 |
| 結論: | 最多十名參賽者是學生。 |
接著我們再看一個涉及「例外結構」的例子,這次我們使用「AAA-1式」:
| 大前提: | all(M)(P) |
| 小前提: | all(S)(M) |
| 結論: | all(S)(P) |
為方便以下的推導,我們首先把上面的大前提和小前提分別表達為|M − P| = 0和S ⊆ M。由於x = 0 ⇒ x ≤ 0並且M − P = M ∩ ~P,我們推得
接著應用定理1(2),容易推得|S ∩ ~P| ≤ 0,這正是上面的結論所要表達的意思。總上所述,我們可以 從|M − P| = 0和S ⊆ M推得|S ∩ ~P| ≤ 0。由於在上述討論中,0沒有任何特殊性,它可以 為任何實數n取代,這實際等同於把上述有效格式中的大前提和結論改為「例外結構」,這樣我們便得到以下這 個有效的「例外結構三段論」格式(註7):
| 大前提: | (all but n)(M)(P) |
| 小前提: | all(S)(M) |
| 結論: | (all but at most n)(S)(P) |
以下推理就是應用這個有效格式的實例:
| 大前提: | 除了三人外,所有參賽者都是會員。 |
| 小前提: | 所有學生都是參賽者。 |
| 結論: | 除了最多三人外,所有學生都是會員。 |
我們還可以對「直言三段論」的其他有效格式進行類似的分析,但由於「三段論」的有效格式共有24個,這將 是繁重的工作,本文的討論只能到此為止。
筆者在《廣義量詞系列:直接推理的革新》定義了「模糊量化句」之間的 蘊涵關係,並提出了一條定理(即上述網頁的定理1)。原則上我們可以把上述定義和定理推廣至「三段論推理」 ,從而推導或證明某些「模糊三段論」的有效格式。舉例說,以下「模糊三段論」推理格式顯然是有 效的:
| 大前提: | all(M)(P) | |
| 小前提: | (a very large proportion of)(S)(M) | (2) |
| 結論: | (at least a small proportion of)(S)(P) |
以下推理就是應用這個有效格式的實例:
| 大前提: | 所有參賽者都是會員。 |
| 小前提: | 非常多學生是參賽者。 |
| 結論: | 至少一小部分學生是會員。 |
現在就讓我們來證明(2)的有效性。為方便討論,以下提供「模糊量詞」"(a very large proportion of)"和"(at least a small proportion of)"的「隸屬度函數」的圖象:

根據(2)的大前提,我們有M ⊆ P。其次,根據前面的定理1(3),我們有
而根據上面μ[(a very large proportion of)](x)的圖象,容易看到
根據筆者在上述網頁定義的式(2),上式等價於
換句話說,我們可以從(2)的大前提和小前提推出「(a very large proportion of)(S)(P)」。另外, 根據上述網頁的式(5),我們有以下「差等關係」:
上面右端的表達式正是(2)的結論,至此我們證明了(2)的有效性。
請注意在上述證明中,我們實際上是利用(2)的大前提把其小前提改寫為「(a very large proportion
of)(S)(P)」,然後再根據一個「差等關係」推出結論,因此上述「模糊三段論」推理實際被歸約為「對當
關係推理」。我們之所以能進行這種歸約,是因為在(2)中,我們利用了「非模糊量詞」"all"的特性,
因此嚴格地說,上述推理並非純粹的「模糊三段論」推理。現在的問題是,我們能否不依賴上述歸約而推導出
純粹的「模糊三段論」有效格式?
筆者在《廣義量詞系列:直接推理的革新》)中指出,如要定義兩個具有不 同「模糊量詞」的語句之間的蘊涵關係,必須確保這兩個語句具有相同的「參項」(詳見上述網頁的式(3))。可 是,傳統的「直言三段論」涉及三個詞項之間錯綜複雜的關係,難以確保「三段論」中的三個命題具有相同的 「參項」。以傳統「三段論」的「第一格」為例,假如我們把「第一格」中三個命題的真值轉化為「隸屬度函 數」的形式,那麼我們有(以下假設Q、Q'和Q''皆表達相對數量):
| 大前提: | μ[Q](|M ∩ P| / |M|) |
| 小前提: | μ[Q'](|S ∩ M| / |S|) |
| 結論: | μ[Q''](|S ∩ P| / |S|) |
由於上面三個命題的「參項」各不相同且不能化約,我們無法界定它們之間的蘊涵關係。由此可見,我們不能
從傳統的「直言三段論」有效格式簡單推出純粹的「模糊三段論」有效格式。
為克服上述困難,Zadeh另闢蹊徑。他從以下「交積三段論」(Intersection / Product Syllogism)推理得到啟
發:
| 前提1: | 剛好80%的學生是單身人士。 |
| 前提2: | 剛好60%的單身學生是男性。 |
| 結論: | 剛好48%的學生是單身男性。 |
請注意由於上述推理已非傳統「直言三段論」的形式,傳統對「大前提」和「小前提」的區分已失去意義,所 以在上面我們把這兩個前提分別稱為「前提1」和「前提2」,而且這兩個前提是可以自由對調的。我們可以把 上述推理抽象為一般形式,並把三個命題寫成「特徵函項」的形式(以下用A、B和C分別代表「學生」、「單身」 和「男性」)(註8):
| 前提1: | χ[(exactly 80%)](|A ∩ B| / |A|) | |
| 前提2: | χ[(exactly 60%)](|A ∩ B ∩ C| / |A ∩ B|) | (3) |
| 結論: | χ[(exactly 48%)](|A ∩ B ∩ C| / |A|) |
請注意如果我們把上面兩個前提的「參項」相乘,便會得到與結論相同的「參項」:
這樣我們便解決了傳統「三段論」格式中前提與結論沒有相同「參項」的問題。不僅如此,上例還顯示如果我 們把兩個前提的「量詞」所代表的實數相乘,便可得到結論的「量詞」所代表的實數:
總上所述,在上述推理中,「參項」與「量詞」具有平行的關係。當「三段論」中三個命題的「參項」存在某
種函數關係時,該三個命題的「量詞」也存在相同的函數關係。Zadeh把上述情況推廣到「模糊量詞」,從而得
到以下的「量詞擴張原理」(Quantifier Extension Principle):
定理2:設有以下「三段論」形式(表達為「隸屬度函數」的形式):
| 前提1: | μ[Q](x) |
| 前提2: | μ[Q'](x') |
| 結論: | μ[Q''](x'') |
如果x'' = f(x, x'),則Q'' = f(Q, Q')。其中f(Q, Q')代表量詞之間的某個函數關係,這個函數與f(x, x')
的關係可用模糊數學上的「擴張原理」(Extension Principle)來定義。
在模糊數學上,「擴張原理」可用來把普通集合元素的函數轉化為模糊集合的函數。設f: X → Y為普通集
合元素的一元函數,那麼我們可以把f轉化為以下函數:設A為X上的模糊集合,則f(A)為Y上的模糊集合,其隸
屬度函數為(在下式中,x ∈ X,y ∈ Y):
| μ[f(A)](y) = | maxf(x) = y μ[A](x), | if f−1(y) ≠ Φ | (4) |
| 0, | if f−1(y) = Φ |
另設f: X × X' → Y為普通集合元素的二元函數,那麼我們可以把f轉化為以下函數:設A和A'分別 為X和X'上的模糊集合,則f(A, A')為Y上的模糊集合,其隸屬度函數為(在下式中,x ∈ X,x' ∈ X' ,y ∈ Y):
| μ[f(A, A')](y) = | maxf(x, x') = y min(μ[A](x), μ[A'](x')), | if f−1(y) ≠ Φ | (5) |
| 0, | if f−1(y) = Φ |
利用上述定理,我們可以嘗試推導某些純粹的「模糊三段論」有效格式。舉例說,我們可以把(3)中兩個前提的 量詞換成「模糊量詞」:
| 前提1: | μ[(slightly more than half of)](|A ∩ B| / |A|) | |
| 前提2: | μ[(slightly less than half of)](|A ∩ B ∩ C| / |A ∩ B|) | (6) |
| 結論: | μ[Q''](|A ∩ B ∩ C| / |A|) |
現在的問題是,上面結論中的Q''是甚麼量詞?根據前面的討論和定理2,我們知道
可是上式右端究竟又代表甚麼意思?為讓讀者易於明白,以下用一個簡化的例子以作說明。設"(slightly more than half of)"的「參項」x和"(slightly less than half of)"的「參項」x'的取值範圍為 離散實數集{0, 0.1 ... 0.9, 1},並且有以下「隸屬度函數」:
(slightly more than half of) × (slightly less than half of)的「參項」y的取值 範圍為{y: ∃x, x' ∈ {0, 0.1 ... 0.9, 1} (y = x × x')} = {0, 0.01, ... 0.9, 1}。由於「×」是二元算子,我們可以用(5)來求上述乘積的「隸屬度函數」。容易看到上述乘積的 絕大多數隸屬度皆為0,以下僅給出一個非0值的計算步驟。設y = 0.18,那麼由於0.18 = 0.2 × 0.9 = 0.3 × 0.6 = 0.6 × 0.3 = 0.9 × 0.2,我們用(5)作以下計算:
| μ[(slightly more than half of) × (slightly less than half of)](0.18) | |
| = | maxx × x' = 0.18 min(μ[(slightly more than half of)](x), μ[(slightly less than half of)](x')) |
| = | max(min(0, 0), min(0, 0), min(1, 0.2), min(0, 0)) |
| = | max(0, 0, 0.2, 0) |
| = | 0.2 |
利用上述方法,我們便可以求得上述乘積的「隸屬度函數」(下式僅列出隸屬度不為0的項):
上式可粗略地看成「模糊量詞」"(about 1/4)"的「隸屬度函數」,這樣我們便可以把"(about 1/4)"代入(6)中的Q''。以下推理是應用(6)的實例:
| 前提1: | 略多於半數學生是單身人士。 |
| 前提2: | 略少於半數單身學生是男性。 |
| 結論: | 約四分一學生是單身男性。 |
當然,並非在所有情況下均可以像上例那樣用一條「等式」把「三段論」的結論與兩個前提聯繫起來,有時我 們充其量只能得到一條「不等式」。但即使在這種情況下,我們仍可運用定理2,只要把該定理中的「等式」 x'' = f(x, x')和Q'' = f(Q, Q')改為相應的「不等式」便行了。舉例說,設有以下推理:
| 前提1: | 幾乎所有學生是單身人士。 |
| 前提2: | 非常多學生是男性。 |
| 結論: | Q''學生是單身或男性。 |
我們可以把上述推理抽象為
| 前提1: | μ[(almost all)](|A ∩ B| / |A|) | ||
| 前提2: | μ[(a very large proportion of)](|A ∩ C| / |A|) | (7) | |
| 結論: | μ[Q''](|A ∩ (B ∪ C)| / |A|) |
由於上述三個「隸屬度函數」的「參項」有相同的分母,我們只需考慮這些「參項」的分子。根據集合論,我 們有以下「不等式」:
根據定理2,我們應有
不過,由於上述的Q''表達相對數量,其「參項」y的值不應超出[0, 1]以外,但在進行上述「+」運算時,其結 果可能大於1。為把上述運算結果限制在[0, 1]之內,我們把上述Q''的定義修改為
上式就是(7)中量詞Q''的形式,我們可以把這個量詞解讀成「最多xxx」,其中的「xxx」由「≤」後面的算 式確定。儘管我們可以用模糊數學的「擴張原理」求得這個「xxx」的「隸屬度函數」,但卻不一定能用簡單的 自然語言表達它。這裡我們看到了「模糊量詞」的局限性,儘管在現實中存在的模糊性有無限種可能程度,但 自然語言中的「模糊量詞」卻很有限,遠遠不能涵蓋各種可能情況。不過,上述情況正是模糊推理的特點。當 代模糊數學對模糊推理(其中包括「模糊三段論」推理)尚有其他研究成果,這裡不能一一詳述。
筆者在《廣義量詞系列:直接推理的革新》中定義了疑問句之間的蘊涵關
係,因此原則上我們可以把上述定義推廣至「三段論推理」,從而推導或證明某些「疑問三段論」的
有效格式。不過,為了與其他「對當關係」的定義相一致,筆者在上述網頁對蘊涵關係採取了較為狹窄的定義
。在此一定義下,凡是沒有相同解答的疑問句之間都談不上蘊涵關係。可是,由於此一定義大大限制了我們所
能考察的疑問句推理,我們有必要在這裡放寬上述定義。
具體地說,我們作出如下定義:疑問句q蘊涵疑問句q',當且僅當對q的每個可能解答a而言,都有q'的某個可能
解答a'使得
請注意在上述定義中,a與a'可以是不同的解答。上述定義反映了如下事實:假如我們可以憑q的真解答a推斷出 q'的真解答a',我們便說q蘊涵q'。根據以上定義,以下蘊涵關係是成立的:
以下讓我們來驗證上述蘊涵關係的有效性。為簡化討論,我們假設論域中的人物只有John、Bill和Mary,並且 只有以下八個「可能世界」:
其中w{j}代表「只有John出席了聚會」的「可能世界」,其餘類推。q1有八個可能解 答:「沒有人」 ... 「John、Bill和Mary」(以下分別記作a1 = Φ ... a1 = {j, b, m}),而且對應於每一個可能解答的「可能世界集合」剛好等於上述八個「可能世界」之一:
| World(q1(Φ)) = {wΦ} | (9) |
| ... | |
| World(q1({j, b, m})) = {w{j, b, m}} |
至於q2,則只有兩個可能解答:「有」和「沒有」(以下分別記作a2 = y和 a2 = n)。對應於這兩個可能解答的「可能世界集合」為:
| World(q2(y)) = {w{j}, w{j, b}, w{j, m}, w{j, b, m}} | (10) |
| World(q2(n)) = {wΦ, w{b}, w{m}, w{b, m}} |
容易看到,上面的(9)和(10)符合(8)的條件,所以q1蘊涵q2。上述結果亦告訴我們 q1和q2的解答之間的對應關係。舉例說,由於World(q1(Φ)) ⊆ World(q2(n)),當q1的真解答為「沒有人」時,我們便可以推斷q2的真解 答為「沒有」。
接著讓我們把上述蘊涵關係推廣為「三段論推理」。「三段論推理」實質上就是兩個前提與結論之間的蘊涵關 係,這兩個前提之間又存在「合取」關係。從「可能世界集合」的角度看,兩個前提的「合取」相當於對應於 這兩個前提的「可能世界集合」的「交集」。綜合以上討論,我們可以作出如下定義:設有疑問句q、q'和q'' ,如果對q的每一可能解答a以及q'的每一可能解答a',都有q''的某個可能解答a''使得
我們便說q、q'和q''構成「疑問三段論」,其中q和q'為前提,q''為結論。
跟「模糊三段論」相似,我們難以構造與傳統「直言三段論」具有相似形式的「疑問三段論」。不過,
Groenendijk和Stokhof在Type-Shifting Rules and the Semantics of Interrogatives一文中提出了
以下推理:
| 前提1: | q3: Whom does Mary love? | (12) |
| 前提2: | q4: Who are the men? | |
| 結論: | q5: Which men does Mary love? |
請注意如果我們把上述推理中的"who(m)"分解成"what + person",並把"men"、"loved by Mary"和 "person"分別看成「小項」、「大項」和「中項」,那麼上述推理在形式上便與傳統的「第三格」三段論推理 很相似。現在讓我們驗證上述推理的有效性,為簡化討論,我們假設論域中的人物只有John和Bill,並且只有 以下16個「可能世界」:
其中w{j}, Φ代表「只有John是男人並且Mary不愛任何人」的「可能世界」,其餘類推。上面 的q3、q4和q5均可以"Nobody"、"John"、"Bill"和"John and Bill"為可 能解答,可分別用Φ、{j}、{b}和{j, b}來代表。但請注意同一個解答在作為不同疑問句的解答時,可能對 應著不同的「可能世界集合」。以解答{j}為例,對應於上述三個疑問句,我們有:
| World(q3({j})) = {wΦ, {j}, w{j}, {j}, w{b}, {j}, w{j, b}, {j}} | (13) |
| World(q4({j})) = {w{j}, Φ, w{j}, {j}, w{j}, {b}, w{j}, {j, b}} | |
| World(q5({j})) = {w{j}, {j}, w{j, b}, {j}} |
請注意上面的World(q5({j}))體現了疑問句的「預設」,因為當我們以"John"回答q5 時,我們預設了John是男人,所以World(q5({j}))不應包括那些John不是男人的「可能世界」,例 如w{b}, {j}。從(13)可以看到,
這反映了如下事實:當某人以"John"作為q3和q4的真解答時,我們可以推斷他對
q5的真解答也必然是"John"。對於其他解答,我們也可作類似驗證,這裡不一一詳述。
我們可以把(12)抽象為以下推理形式(在下式中,A、A'和A''為「解答論元」):
| 前提1: | who(−)(P)(A) | |
| 前提2: | who(−)(S)(A') | |
| 結論: | which(S)(P)(A'') |
可以證明上述「三段論」是有效的推理形式。有關「疑問三段論」的其他有效格式乃至疑問推理的一般原理, 尚有待進一步的研究。
筆者在《廣義量詞系列:空間量化結構》中指出,"inside"、"outside"和
"overlapping"分別與量詞"all" 、 "no" 和"some"相對應,因此我們可以為含有這些
詞項的命題構造相應的「三段論推理」。筆者在上述網頁中亦指出,自然語言中的其他「方位介詞」在某種程
度上也與量詞存在對應關係。由此我們可以推斷,應可把「三段論推理」推廣至這些「方位介詞」,從而構造
出一些有效的「空間三段論」推理模式,本節將探討這個問題。
雖然筆者在上述網頁中指出,絕大多數「方位介詞」都含有"outside"的語義,但這並不代表這些介詞具有與
"no"完全相同的推理模式。舉例說,很多「方位介詞」(例如"above")都具有「傳遞性」,即符合以下
推理模式(以下把含有「方位介詞」的語句寫成「三分結構式」):
| 大前提: | above(M)(P) | (14) |
| 小前提: | above(S)(M) | |
| 結論: | above(S)(P) |
在這一方面,"above"等介詞與"all"具有相似的推理模式(試比較上述推理與傳統「三段論」的「AAA-1 式」):
| 大前提: | all(M)(P) |
| 小前提: | all(S)(M) |
| 結論: | all(S)(P) |
而與"no"的推理模式不相似(「EEE-1式」並非有效的推理模式)。
可是,我們亦發現某些介詞在某些方面與"no"有相似的推理模式,例如"far away from"便符合以下推
理模式:
| 大前提: | inside(P)(M) | (15) |
| 小前提: | (far away from)(S)(M) | |
| 結論: | (far away from)(S)(P) |
請注意上述推理模式與傳統「三段論」的「AEE-2式」非常相似:
| 大前提: | all(P)(M) |
| 小前提: | no(S)(M) |
| 結論: | no(S)(P) |
事實上,「方位介詞」的推理模式與量詞的對應關係是錯綜複雜的。某一介詞的推理模式可能在某一方面與某
一量詞相似,在另一方面卻與另一量詞相似,因此我們不能把"inside"、"outside"以外的任一「方位介詞」簡
單比附作某一量詞,而必須根據某一介詞的語義論證該介詞在某一推理模式中的有效性,以下筆者運用上述方
法驗證上面(14)和(15)的有效性。
首先考慮(14),根據上述網頁,我們可以把(14)的大前提表達為
但上式過於繁複,不方便進行推理,所以以下改用文字與符號夾雜的方法。為簡化討論,以下只考慮一個特殊 情況,就是假設S、P和M僅包含平面上的一個點。為易於理解,讀者可參考下圖:

經上述簡化後,我們可以把(14)的大前提和小前提分別理解為:有一個向量v從P點指向M點和另一個向 量v'從M點指向S點,並且
接著求上述兩個向量的和:v'' = v + v',v''就是由P點指向S點的向量。根據 向量「內積」的特性,我們有
另外,根據向量的加法,我們有v''up = vup + v'up以及v''⊥up = v⊥up + v'⊥up。由於v • up > 0和v' • up > 0, 我們有|v''up| = |vup + v'up| = |vup| + |v'up|。根據上述兩個前提,我們又有 |vup| + |v'up| > |v⊥up| + |v'⊥up|。最後利用不等式
我們得到|v⊥up| + |v'⊥up| ≥ |v⊥up + v'⊥up| = |v''⊥up|。 由此最終得到
綜合以上結果,(14)的結論得證,至此我們驗證了(14)的有效性。
接著考慮(15),為易於理解,讀者可參考下圖:

沿用上述網頁的定義,我們把(15)的小前提理解為
其中s代表某個長度標準。接著,根據(15)的大前提,由於所有P的點都是M的點,我們必有
由此必有
即
(15)的結論乃得證,至此我們驗證了(15)的有效性。
以上兩例顯示,如要發掘或證明「空間三段論」,須綜合運用「向量空間語義學」、數學以及邏輯學的知識,
筆者認為這方面的研究尚有廣闊的空間,有待學者探討。
筆者在《廣義量詞系列:相關詞與度量結構》中介紹了「混合量化結構」 ,這種結構涉及多種論域。與此相對應,我們也可討論「混合三段論」,即涉及多種論域的「三段 論推理」,其中一種「混合三段論」就是「模態邏輯」中的某些「模態三段論」。其實筆者在 《廣義量詞系列:古典推理模式》中已介紹過「模態三段論」,當時筆者 指出,並非所有「模態三段論」都可透過把「直言三段論」的24種有效格式推廣到「可能世界論域」而得到, 這是因為某些「模態三段論」在實質上是「混合三段論」。試看以下顯然有效的推理模式:
| 大前提: | 所有M必然都是P。 | (16) |
| 小前提: | 有S可能是M。 | |
| 結論: | 有S可能是P。 |
請注意上述推理混合了「個體論域」和「可能世界論域」上的量詞,無法表達為傳統「直言三段論」的格式。 因此為證明(16)的有效性,我們必須借助「廣義量詞理論」和「可能世界語義學」的某些定義。首先,根據上 面的小前提,我們知道在至少一個「可能世界」中命題「有S是M」是真的,假設這個「可能世界」是w,換句話 說,在w中以下「三分結構式」是真的:
其次,根據上面的大前提,在所有「可能世界」中命題「所有M都是P」是真的,這意味著在w中,以下「三分結 構式」也是真的:
接著,利用「直言三段論」的「AII-1式」,我們可以從以上兩個「三分結構式」推得,在w中以下「三分結構 式」也是真的:
換句話說,命題「有S是P」在至少一個「可能世界」中是真的,這正是上面的結論,由此證明了(16)的有效性
。
其他「模態三段論」有效格式也可使用類似的方法證明。除了「模態三段論」外,筆者認為還應存在其他類型
的「混合三段論」,但學界對這方面還沒有系統的研究,因此對此一課題的討論只能到此為止。
在這最後一節,筆者將簡介包含某些複雜量詞(包括「結構化量詞」和「迭代量詞」)的「三段論推理」。由於 這是一個鮮有學者涉足的領域,尚無系統的研究,以下筆者只提供一些零星的有效推理模式及部分證明。 Keenan在Excursions in Natural Logic一文中提出了一個包含「<12,1>型結構化量詞」 "(more ... than ...)"的「三段論推理」有效格式:
| 前提1: | (more ... than ...)(A, B)(D) | (17) |
| 前提2: | (more ... than ...)(B, C)(D) | |
| 結論: | (more ... than ...)(A, C)(D) |
以下是這個推理模式的實例:
| 前提1: | More students than teachers signed the petition. |
| 前提2: | More teachers than deans signed the petition. |
| 結論: | More students than deans signed the petition. |
請注意(17)是容易證明的,根據「結構化量詞」的真值條件,我們可以把(17)的兩個前提分別表達為|A ∩
D| > |B ∩ D|和|B ∩ D| > |C ∩ D|。接著,根據「>」的「傳遞性」,我們有|A ∩ D| > |C
∩ D|,這正是(17)的結論。
Keenan還指出,可把(17)中的量詞改為"(fewer ... than ...)"或"(exactly as many ... as
...)"等,推理模式仍然有效。此外,他還提出以下有效推理模式:
| 前提1: | (exactly n more ... than ...)(A, B)(D) |
| 前提2: | (exactly m more ... than ...)(B, C)(D) |
| 結論: | (exactly (n + m) more ... than ...)(A, C)(D) |
讀者不妨自行證明上述模式的有效性。
Peterson在其著作中介紹了「關係命題」(即包含「迭代量詞」的命題)的「三段論推理」,這種推理的結論一
般都包含一個關係分句。儘管他為這種推理提供了一套推理規則,但他沒有為這些規則提供數學論證,因此本
文不擬引述他的推理規則。以下只提供一個簡單的「迭代量詞三段論」的實例:
| 前提1: | 有一個男孩每個女孩他都愛。 |
| 前提2: | 有一個女孩迷戀最少三個明星。 |
| 結論: | 有一個男孩愛一個迷戀最少三個明星的女孩。 |
容易看到上述推理是有效的,因為根據前提1,我們可以假定有一個男孩b,他愛每一個女孩。另外,根據前提2
,我們可以假定有一個女孩g,她迷戀最少三個明星;而且由於g是女孩,她為b所愛。換句話說,b愛一個迷戀
最少三個明星的女孩,因此結論得證。
上述例子顯示,要證明個別含複雜量詞的「三段論推理」並不困難,但由於這類推理中的三個命題比傳統推理
包含較多的詞項或量詞,如要逐一考察各種可能推理模式的有效性,這將是繁重的工作,還有待學者作進一步
研究。


