Raios X
Tomografia de raios X
Qualidade de imagens
Laboratório
Caracterização do sistema
Madeira
Referências
Autor
Tomografia de raios X
Reconstrução de imagens
Segundo o Teorema da Projeção de Fourier, a transformada de Fourier de uma projeção que forma um ângulo q com o eixo x fornece os valores da transformada bidimensional do objeto ao longo de uma linha radial formando o mesmo ângulo com o eixo u. Desta forma, calculando a transformada de Fourier de um numero grande de projeções formando vários ângulos com o eixo x, obtém-se os valores da transformada bidimensional do objeto ao longo de várias linhas radiais:

[Fig. 1] Pontos da transformada bidimensional
obtidos a partir da transformada de várias projeções.
É possível obter a imagem da seção reta original a partir desta distribuição de pontos. Para isso, são necessárias duas etapas: (a) uma interpolação de forma a obter pontos distribuidos em coordenadas cartesianas e (b) a transformada bidimensional de Fourier inversa, fornecendo os valores da imagem no domínio do espaço. Este método é conhecido como reconstrução direta de Fourier (direct Fourier reconstruction).
Devido à dificuldade de interpolação de coordenadas polares para coordenadas cartesianas, esta técnica de reconstrução é pouco empregada.
A técnica mais conhecida e utilizada de reconstrução de imagens é a retroprojeção filtrada (filtered backprojection). Como será visto a seguir, este método, que tem como fundamento o Teorema da Projeção, faz proveito de uma mudança de coordenadas dos argumentos da transformada bidimensional inversa de Fourier.
A transformada de Fourier inversa de duas dimensões é dada pela equação (12):
 (12)
(12)Transformando esta expressão de coordenadas cartesianas (u,v) para coordenadas polares (w,q),
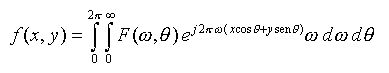 (13)
(13)Separando os limites da integral acima de 0 até p e de p até 2p, obtém-se a equação (14):
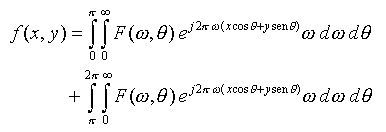
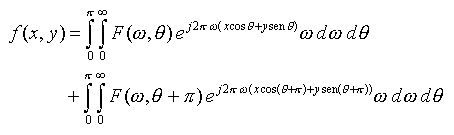 (14)
(14)A transformada de Fourier em coordenadas polares obedece à seguinte propriedade:
A substituição desta propriedade na equação (14) resulta na equação (16):
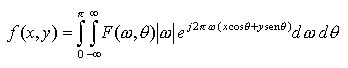 (16)
(16)Aplicando o Teorema da Projeção (equação 11) na equação acima, obtém-se:
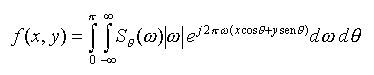
ou
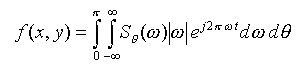 (17)
(17)Esta expressão é a equação principal do método da retroprojeção filtrada. Este nome surge da interpretação da equaçao (17) ao ser dividida em duas integrais:
 (18)
(18)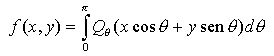 (19)
(19)A equação (18) é a transformada inversa de Fourier do produto Sq (w)|w|. Esta multiplicação representa a filtragem da projeção Pq (t) (cuja transformada é Sq (w)) pela função |w|. Qq (t) é denominada projeção filtrada. O gráfico do filtro |w|, conhecido como filtro rampa, está apresentado na figura abaixo. Este filtro também é conhecido como filtro de Ramachandran-Lakshminarayanan, ou simplesmente filtro Ram-Lak.
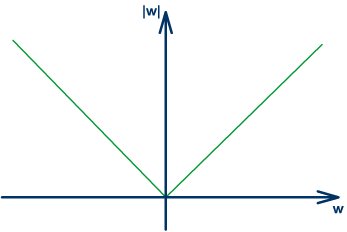
[Fig. 2] Filtro rampa.
A equação (19) representa a operação de retroprojeção das projeções filtradas Qq(t). O valor de um determinado ponto de coordenadas (x,y) da imagem original é dado pelo somatório (ou integral) dos diversos valores Qq (xcosq + ysenq), para q variando de 0 a p. A figura 3 mostra o significado da contribuição de uma projeção filtrada Qq1(t) qualquer.
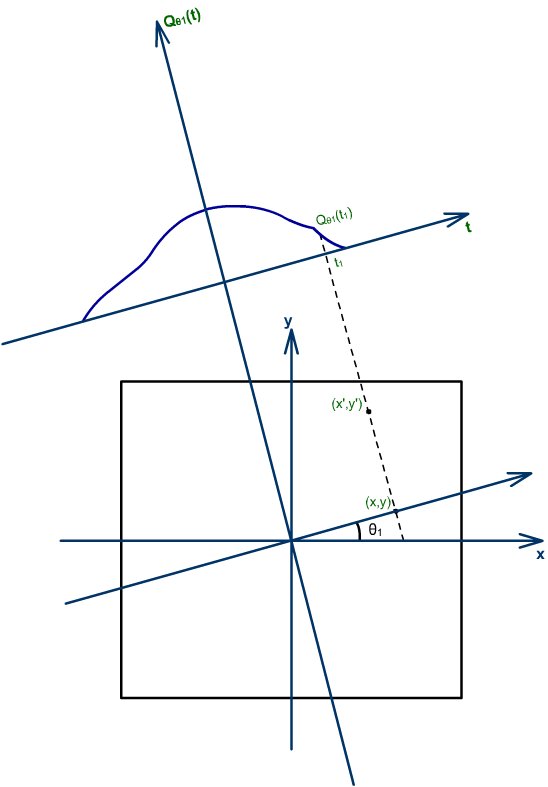
[Fig. 3] Retroprojeção para reconstrução de uma imagem.
Para o ângulo q1, o valor da projeção filtrada Qq1(t) que contribuirá para o valor final no ponto (x,y) é dado pela coordenada t1 = xcosq1 + ysenq1. Para o mesmo ângulo q1 e o ponto (x',y'), o valor da coordenada t será o mesmo: t1' = x'cosq1 + y'senq1 = t1.
Portanto, o valor da projeção filtrada Qq1(t1) é retroprojetado na região da imagem original, contribuindo para todos os pontos ao longo da reta t = t1. Todos os valores de Qq1(t) são desta maneira retroprojetados na região da imagem original. Este processo é realizado para todos os ângulos qi em que foram adquiridas as projeções Pqi.