Sistema de Particulas en OpenGL

Una particula es un objeto que tiene masa, posicion, velocidad y puede estar afectada por fuerzas exteriores, como por ejemplo la aceleracion de la gravedad, la resistendia del aire o el viento. En este tutorial vamos a desarrollar un sistema de particulas basico, donde la unica fuerza exterior que actua sobre las particulas es la gravedad.

La Inicializacion
Para definir nuestra particula, necesitamos lo siguiente su posicion, velocidad, aceleracion, un color, el "tiempo" de vida, y lo rapido que su vida se termina :-(, nos podemos olvidar de su masa, eso lo tenemos en cuenta solo cuando las particulas interaccionan entre ellas.

Estructura que define la particula:

typedef struct {
	float	life;		// la duracion de su vida
	float	fade;		// lo rapido que se termina su vida
	float	r, g, b;    // color
	GLfloat x, y, z;    // posicion
	GLfloat vx, vy, vz; // velocidad 
    GLfloat ax, ay, az; // aceleracion
} Particle;

y nuestro sistema de particulas, en este caso 1000:

#define MAX_PARTICULAS  1000
Particle particula[MAX_PARTICULAS];

listo ya tenemos nuestro sistema definido ahora lo tenemos que inicializar, es decir darle las condiciones iniciales para la posicion, velocidad, aceleracion, color, vida a cada una de las particulas:

void iniParticulas(void)
{
 GLfloat v, theta, phi;
 int i;

 for(i=0; i<MAX_PARTICULAS; i++)
    {
	v = 0.8*frand()+0.2;
    phi = frand()*M_PI;
    theta = 2.0*frand()*M_PI;
    particula[i].x = 0.0f;
    particula[i].y = 50.0f;
    particula[i].z = 0.0f;
    particula[i].vx = v * cos(theta) * sin(phi);
    particula[i].vy = v * cos(phi);
    particula[i].vz = v * sin(theta) * sin(phi);
	particula[i].ax =  0.01f;
    particula[i].ay = -0.08f;
    particula[i].az =  0.0f;
	particula[i].r = 0.882f;
	particula[i].g = 0.552f;	
	particula[i].b = 0.211f;	
	particula[i].life = 1.0f;		                
	particula[i].fade = 0.01f;
	}
}

explico un poco esto, como sabran en el sistema de coordenadas de OpenGL la coordenada Y es la que apunta hacia "arriba", entonces todas mis particulas van a "nacer" en el punto de coordenadas 0, 30, 0, y con una velocidad inicial que varia entre 0.1 y 1 con una distribucion del tipo esferico, las unica fuerza que interviene es la gravedad y actua en la direccion negativa del eje Y, va no puedo utilizare su valor de 9,8 m/s2, basta con tomar por ejemplo un valor negativo, yo tome -0.075, y tambien agrego algo de "viento", que en realidad es una pequeña fuerza que actua en el sentido positivo del eje X, como mi intencion no es crear una simulacion realista, solo quiero que se vea el efecto del movimiento de las particulas, para obtener valores realista, abria que trabajar con valores escalados de las unidades por ejemplo la gravedad y utilizar un metodo mas presizo para la solucion de la simulacion por ejemplo Runge-Kutta.

La simulacion

Primero tenemos que plantear las ecuaciones que describen el sistema, no vasamos en las leyes de Newton de la dinamica , vamos a obtener un sistema de ecuaciones diferenciales las que vamos a resolver numericamente utilizando el Metodo de Euler.

El movimiento de una particula bajo la accion de la gravedad esta descrito por el siguiente sistema de ecuaciones diferenciales:

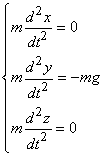
con las siguientes condiciones iniciales para t = 0, donde v es la velocidad incicial y theta, phi son angulos que definen la direcion del vector velocidad en el que se dispara la particula

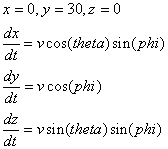
solo nos resta aplicar Euler al sistema para obtener el algoritmo que me calcula la simulacion del movimiento de todas las particulas. En la seccion de Matematicas tenes algunos ejemplos de como hacer esto :-), la porcion de codigo de abajo rsuleve el sistema:

void display(void)
{
 ...
 for (i=0; i<MAX_PARTICULAS; i++)
	{
	...
	//aqui dibujo la particula
	...
	particula[i].x += particula[i].vx;
    particula[i].y += particula[i].vy;
    particula[i].z += particula[i].vz;
    particula[i].vx += particula[i].ax;
    particula[i].vy += particula[i].ay;
    particula[i].vz += particula[i].az;
	...	
	}
...
}

El Dibujo de la Particula

Podria simplemente representar la particula como un pixels de un determinado color en la pantalla pero no, lo vamos a hacer un poco mas complicado, vamos a crear un poligono rectangular a partir de la posicion (x,y) de la particula, vamos a utilizar una imagen en formato bmp como textura.

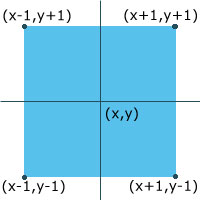
Poligono rectangular utilizado para representar las particulas, la coordenada z permanece constante, por eso no la represento aqui, en este grafico.

La imagen utilizada como textura.

porcion del codigo en OpenGL, para representar la particula:

...
glColor4f(particula[i].r,particula[i].g,particula[i].b, particula[i].life);
glBegin(GL_TRIANGLE_STRIP);				        
	glTexCoord2d(1,1); glVertex3f(particula[i].x+1.0f,particula[i].y+1.0f,particula[i].z);        
	glTexCoord2d(0,1); glVertex3f(particula[i].x-1.0f,particula[i].y+1.0f,particula[i].z);         
	glTexCoord2d(1,0); glVertex3f(particula[i].x+1.0f,particula[i].y-1.0f,particula[i].z);         
	glTexCoord2d(0,0); glVertex3f(particula[i].x-1.0f,particula[i].y-1.0f,particula[i].z);          
glEnd();
...

Algunas imagenes del programa

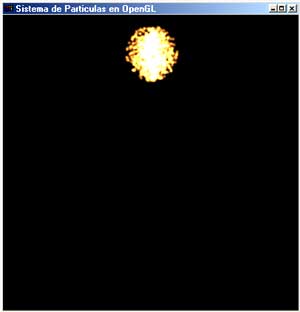
El codigo

El codigo fuente esta en VisualC++ 6.0, utilizo las librerias OpenGL y Glut, todos los archivos necesarios para la compilacion y ejecucion estan en el zip, basta con abrir desde el VisualC++ el archivo Particulas.dsw.

No te olvides de incluir las siguientes librerias glaux.lib, glut32.lib, opengl32.lib en Project > Settings > Links en Object/library modules

Descargas
Codigo Fuente (6 kb)
Ejecutable (53 Kb)

#include <GL/glut.h>
#include <GL/glaux.h>
#include <stdlib.h>
#include <math.h>
#include "textura.h"

#define frand()			((float)rand()/RAND_MAX)
#define M_PI			3.14159265
#define MAX_PARTICULAS  1000

typedef struct {
	float	life;		// vida
	float	fade;		// fade
	float	r, g, b;    // color
	GLfloat x, y, z;    // posicion
	GLfloat vx, vy, vz; // velocidad 
    GLfloat ax, ay, az; // aceleracion
} Particle;

Particle particula[MAX_PARTICULAS];

char *nombre_archivo_bmp="Particle.bmp";
COGLTexture MyTextura;

void iniTextura(char *archivo_bmp)
{
 MyTextura.LoadFromFile(archivo_bmp);
 glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,GL_LINEAR);
 glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,GL_LINEAR);
}

void iniParticulas(void)
{
 GLfloat v, theta, phi;
 int i;

 for(i=0; i<MAX_PARTICULAS; i++)
    {
	v = 0.8*frand()+0.2;
    phi = frand()*M_PI;
    theta = 2.0*frand()*M_PI;
    particula[i].x = 0.0f;
    particula[i].y = 50.0f;
    particula[i].z = 0.0f;
    particula[i].vx = v * cos(theta) * sin(phi);
    particula[i].vy = v * cos(phi);
    particula[i].vz = v * sin(theta) * sin(phi);
	particula[i].ax =  0.01f;
    particula[i].ay = -0.08f;
    particula[i].az =  0.0f;
	particula[i].r = 0.882f;
	particula[i].g = 0.552f;	
	particula[i].b = 0.211f;	
	particula[i].life = 1.0f;		                
	particula[i].fade = 0.01f;	
	}
}

void iniOpenGL(void)
{
 glClearColor(0.0f,0.0f,0.0f,0.0f);      
 glDisable(GL_DEPTH_TEST);
 glEnable(GL_BLEND);	        		
 glBlendFunc(GL_SRC_ALPHA,GL_ONE);	
 glHint(GL_PERSPECTIVE_CORRECTION_HINT,GL_NICEST);
 iniTextura(nombre_archivo_bmp);
 iniParticulas();
}

void display(void)
{
 int i;

 glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
 glLoadIdentity();
 gluLookAt (0.0, 0.0, 150.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);

 glEnable(GL_TEXTURE_2D);
 MyTextura.SetActive();
 for (i=0; i<MAX_PARTICULAS; i++)
	{
	glColor4f(particula[i].r,particula[i].g,particula[i].b, particula[i].life);
	glBegin(GL_TRIANGLE_STRIP);				        
		glTexCoord2d(1,1); glVertex3f(particula[i].x+1.0f,particula[i].y+1.0f,particula[i].z);            
		glTexCoord2d(0,1); glVertex3f(particula[i].x-1.0f,particula[i].y+1.0f,particula[i].z);       
		glTexCoord2d(1,0); glVertex3f(particula[i].x+1.0f,particula[i].y-1.0f,particula[i].z);        
		glTexCoord2d(0,0); glVertex3f(particula[i].x-1.0f,particula[i].y-1.0f,particula[i].z);      
	glEnd();	
	particula[i].x += particula[i].vx;
    particula[i].y += particula[i].vy;
    particula[i].z += particula[i].vz;
    particula[i].vx += particula[i].ax;
    particula[i].vy += particula[i].ay;
    particula[i].vz += particula[i].az;
	particula[i].life -= particula[i].fade;	
	}
 glutSwapBuffers();
}

void idle(void)
{
 glutPostRedisplay();
}

void reshape(int w, int h)
{
 if (!h)
    return;
 glViewport(0, 0,  (GLsizei) w, (GLsizei) h);
 glMatrixMode(GL_PROJECTION);
 glLoadIdentity();
 gluPerspective(45.0f,(GLfloat)w/(GLfloat)h,0.1f,400.0f);
 glMatrixMode(GL_MODELVIEW);
 glLoadIdentity();
}

void keyboard(unsigned char key, int x, int y)
{
 switch (key)
   {
	case 'e':
	iniParticulas();
	break;
	case 27: exit(0);
    break;
   }
}

int main(int argc, char **argv)
{
 glutInit(&argc, argv);
 glutInitDisplayMode (GLUT_DOUBLE | GLUT_RGB);
 glutInitWindowSize (400, 400);
 glutInitWindowPosition (0, 0);
 glutCreateWindow ("Sistema de Particulas en OpenGL");
 iniOpenGL();
 glutDisplayFunc(display);
 glutReshapeFunc(reshape);
 glutKeyboardFunc(keyboard);
 glutIdleFunc(idle);
 glutMainLoop();
 return 0;
}