Principal | Gráficos 3D | Gráficos 2D | Fractales | Math | Códigos | Tutoriales | Links

Rossler Attractor

Una de las construcciones geométricas más sencillas de CAOS en sistemas contínuos es el sistema de ecuaciones diferenciales de Rossler:

dx/dt = -y -z 
dy/dt = x + a*y 
dz/dt = b + z*(x - c)

donde a=0.2, b=0.2 y c=5.7 son.

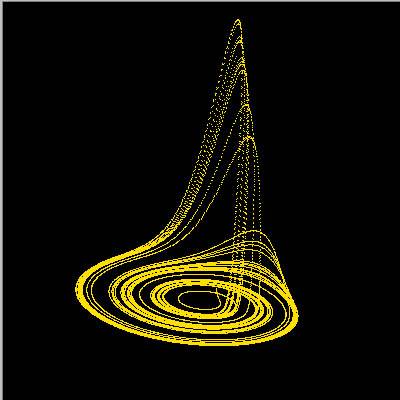
Si se grafican los valores en el plano x,y,z paramétricamente con el tiempo, se obtiene una gráfica, en la que se puede observar que el sistema no converge ni a un punto fijo, ni a un ciclo, sino sigue "dando vueltas" alrededor del atractor.

Rossler Attractor en Visual Basic 5.0

Como se trata de un sistema de ecuaciones diferenciales utilizó el Método de Euler para resolverlo en forma númerica, con las siguientes condiciones iniciales x(0)=1.0, y(0)=1.0, z(0)=1.0 y un tamañao de paso h=0.01, con 30.000 puntos.

rossler1.jpg
r1=1.2, r2=-1.5, r3=0.0

donde r1, r2, r3 son la rotación con respecto a los ejes x, y, z respectivamente en radianes.

Código Fuente

El código esta en VisualBasic 5.0 rossler.zip (2 Kb)

Option Explicit
Const MaxPuntos = 30000
Const FactorDeEscala = 3.5

Dim r1, r2, r3 As Double
Dim sr1, sr2, sr3, cr1, cr2, cr3 As Double
Dim sx, sy As Double
Dim ScreenX, ScreenY As Long

Function dx(ByVal x As Double, ByVal y As Double, ByVal z As Double) As Double
dx = -y - z
End Function

Function dy(ByVal x As Double, ByVal y As Double, ByVal z As Double) As Double
dy = x + 0.2 * y
End Function

Function dz(ByVal x As Double, ByVal y As Double, ByVal z As Double) As Double
dz = 0.2 + z * (x - 5.7)
End Function

Sub SinCos()
sr1 = Sin(r1)
sr2 = Sin(r2)
sr3 = Sin(r3)
cr1 = Cos(r1)
cr2 = Cos(r2)
cr3 = Cos(r3)
End Sub

Sub Calc3D(ByVal x As Double, ByVal y As Double, ByVal z As Double)
Dim xa, ya, za As Double
x = FactorDeEscala * x
y = FactorDeEscala * y
z = FactorDeEscala * z
x = (-1#) * x
xa = cr1 * x - sr1 * z
za = sr1 * x + cr1 * z
x = cr2 * xa + sr2 * y
ya = cr2 * y - sr2 * xa
z = cr3 * za - sr3 * ya
y = sr3 * za + cr3 * ya
z = z - 350
sx = (1200 * x) / z
sy = (1200 * y) / z
End Sub

Sub Rossler()
Dim x, y, z As Double
Dim h As Double
Dim nPuntos As Long

Call SinCos
x = 1#
y = 1#
z = 1#
nPuntos = 0
h = 0.01
Do While (nPuntos < MaxPuntos)
    x = x + h * dx(x, y, z)
    y = y + h * dy(x, y, z)
    z = z + h * dz(x, y, z)
    Call Calc3D(x, y, z)
    sx = sx + ScreenX / 2#
    sy = (sy + ScreenY / 2#) - 100
    Picture1.PSet (sx, ScreenY - sy), RGB(255, 225, 0)
    nPuntos = nPuntos + 1
Loop
End Sub

Private Sub cmdEjecutar_Click()
r1 = 1.2
r2 = -1.5
r3 = 0#
Call Rossler
End Sub

Private Sub cmdSalir_Click()
Unload Me
End Sub

Private Sub Form_Load()
Picture1.BackColor = &H0&
Picture1.ScaleMode = 3
ScreenX = Picture1.ScaleWidth
ScreenY = Picture1.ScaleHeight
End Sub

Rossler Attractor en Visual C++ 5.0 usando OpenGL

Utilizó el Método de Euler , las condiciones iniciales son las mismas x(0)=1.0, y(0)=1.0, z(0)=1.0 y un tamañao de paso h=0.02, con 3.850 esferas.


rossler2.jpg
gluLookAt (0.0, -20.0, 37.0, 0.0, 12.0, 0.0, 0.0, 1.0, 0.0)

rossler3.jpg
gluLookAt (0.0, 0.0, 37.5, 7.5, 0.0, 0.0, 0.0, 1.0, 0.0)

Código Fuente

Todos los archivos necesarios para la compilacion del código se encuentran en rossler_c.zip (3 Kb)

La libreria GLUT 3.6 se la puede encontrar en http://reality.sgi.com/opengl/glut3/glut3.html

Acerca de la instalcion de GLUT, se debe decomprimir el archivo glutdlls36.zip y copiar el archivo GLUT32.DLL en el directorio WINDOWS/SYSTEM, copiar el archivo GLUT32.LIB en el subdirectorio del compilador destinado a las librerias, y el archivo GLUT.H junto con el resto de los includes de OpenGL.

#include <GL/glut.h>
#include <stdlib.h>

GLfloat diffuseMaterial[4] = {0.5, 0.5, 0.5, 1.0};

void init(void) 
{
   GLfloat mat_specular[] = {1.0, 1.0, 1.0, 1.0};
   GLfloat light_position[] = {1.0, 1.0, 1.0, 0.0};

   glClearColor (0.0, 0.0, 0.0, 0.0);
   glShadeModel (GL_SMOOTH);
   glEnable(GL_DEPTH_TEST);
   glMaterialfv(GL_FRONT, GL_DIFFUSE, diffuseMaterial);
   glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
   glMaterialf(GL_FRONT, GL_SHININESS, 25.0);

   glLightfv(GL_LIGHT0, GL_POSITION, light_position);
   glEnable(GL_LIGHTING);
   glEnable(GL_LIGHT0);

   glColorMaterial(GL_FRONT, GL_DIFFUSE);
   glEnable(GL_COLOR_MATERIAL);
}

void display(void)
{
   GLfloat x0, y0, z0, x1, y1, z1;
   GLfloat h;
   int Puntos, MaxPuntos=3850;

   glClear (GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
   glColor3f (1.0, 1.0, 1.0);
   glLoadIdentity ();            
   gluLookAt (0.0, -20.0, 37.0, 0.0, 12.0, 0.0, 0.0, 1.0, 0.0);
   glColor3f(0.2f, 0.8f, 0.8f);
   x0=1.0f;
   y0=1.0f;
   z0=1.0f;
   Puntos=0;
   h=0.02f;
   while  (Puntos<MaxPuntos)
        {
         x1=x0+h*(-y0-z0);
         y1=y0+h*(x0 + 0.2*y0);
         z1=z0+h*(0.2 + z0*(x0-5.7));
         x0=x1;
         y0=y1;
         z0=z1;
         glPushMatrix();
         glTranslatef(x0, y0, z0);
         glutSolidSphere(0.20, 12.0, 12.0);
         glPopMatrix();
         Puntos=Puntos+1;
        }
   glFlush ();
}

void reshape (int w, int h)
{
   glViewport (0, 0, (GLsizei) w, (GLsizei) h); 
   glMatrixMode (GL_PROJECTION);
   glLoadIdentity ();
   glFrustum (-1.0, 1.0, -1.0, 1.0, 1.5, 200.0);
   glMatrixMode (GL_MODELVIEW);
}

/* ARGSUSED1 */
void keyboard(unsigned char key, int x, int y)
{
   switch (key) {
      case 27:
         exit(0);
         break;
   }
}

int main(int argc, char** argv)
{
   glutInit(&argc, argv);
   glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
   glutInitWindowSize (600, 600); 
   glutInitWindowPosition (0, 0);
   glutCreateWindow (argv[0]);
   init ();
   glutDisplayFunc(display); 
   glutReshapeFunc(reshape);
   glutKeyboardFunc(keyboard);
   glutMainLoop();
   return 0;
}


valcoey@hotmail.com

Ramiro Alcocer, 2001

Principal | Gráficos 3D | Gráficos 2D | Fractales | Math | Códigos | Tutoriales | Links