2. DYNAMIKA PŘÍMAČARÝCH A KŘOVIČARÝCH POHYBŮ HMOTNÉHO BODU A SOUSTAV HMOTNÝCH BODŮ
Dynamika vysvětluje příčiny změn pohybového stavu tělesa vzájemným působením okolních těles nebo fyzikálních polí. Toto působení popisuje fyzikální veličina síla F. Síla F je jednoznačně určena působištěm, velikostí a směrem. Jednotkou síly newton (N).
Základními zákony dynamiky hmotného bodu jsou Newtonovy pohybové zákony. Pohybový stav hmotného bodu popisuje fyzikální veličina hybnost p = mv. Jednotlou hybnosti je kg.m.s -1.
Podle druhého pohybového zákona se síla F rovná časové změně hybnosti, tedy F = 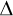 p.( p.(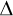 t -1. Jestliže se hmotnost hmotného bodu za dobu DXTt nemění, pak platí t -1. Jestliže se hmotnost hmotného bodu za dobu DXTt nemění, pak platí
F = DXTp.(DXTt)x-1x = DXT(mv).)DXTt)x-1x = m.DXTv.(DXTt)x-1x = ma.
Pro zrychlení platí vztah a = F.mx-1x
Síla, kterou hmotný bod nebo těleso působí na podložku nebo závěs se nazývá tíhová síla tělesa G. Síla, kterou působí Země na hmotný bod nebo na těleso, se nazývá tíhová síla FG = mg.
Síly skládáme jako vektory. Výslednice sil F = F1 + 2 + 3 + ... + n závisí na velikosti skládaných sil a na velikosti úhlu, který svírají vektorové přímky těchto sil. Působí-li na hmotný bod soustava sil, jejichž výslednice je nulová, je také zrychlení nulové a hybnost i rychlost hmotného bodu je vzhledem k inerciální soustavě stálá.
V inerciální vztažné soustavě platí zákon zachování hybnosti: Součet hybností těles izolované soustavy je stálý. Změní-li se hybnost jednoho tělesa, musí se změnit hybnost některého z dalších těles soupravy.
V izolovanéj soustavě dvou těles o hmotnostech m a M platí pro změnu hybností
DXT(mv1 + DXT}Mv2 = 0
Koná-li hmotný bod nebo těleso přímočarý pohyb, může na něj působit jiné těleso nebo pole tak, že síla má buď směr jeho pohybu (hmotný bod nebo těleso se pak pohybuje se zrychlením ve směru rychlosti), nebo směr proti jeho pohybu (hmotný bodnebo těleso se pak pohybuje se zrychlením proti směru rychlosti, koná hmotný bod rovnoměrný pohyb po kružnici. Síla, která tento pohyb způsobuje se nazývá dostředivá síla. Pohybuje-li se hmotný bod o hmotnosti m po kružnici o poloměru r stálou rychlostí o velikosti v, pak pro velikost dostředivé síly platí vtahy
Fd = mad = mv2.r-1 = mr 2 = 4 2 = 4 2r.T -2 = 4 2r.T -2 = 4 2f 2r, 2f 2r,
přičemž  je úhlová rychlost, T oběžná doba neboli perioda a f frekvence rovnoměrného pohybu hmotného bodu po kružnici. je úhlová rychlost, T oběžná doba neboli perioda a f frekvence rovnoměrného pohybu hmotného bodu po kružnici.
V neinerciálních soustavách, které se vzhledem k inerciální vztažné soustavě pohybují se zrychlením, působí setrvačné síly Fysy, přičemž Fysy = -ma, kde a je zrychlení neinerciální soustavy. V neinerciálích vztažných soustavách neplatí Newtonovy pohybové zákony.
Ve vztažné soustavě, která se vzhledem k inerciální soustavě rovnoměrně otáčí, vzniká setrvačná dostředivá síla F0 = -Fd. Setrvačná odostředivá síla působí na hmotný bod ve směru od středu kružnicové trajektorie. Pro velikost odstředivé síly platí tytéž vztahy jako pro velikost dostředivé síly.
| 


