3. ENERGIE HMOTNÝCH BODŮ
Dráhový účinek síly působící na těleso popisujeme veličinou mechanická práce W. Jestliže je F velikost síly a s dráha, kterou těleso působením síly urazí, přičemž síla a posunutí mají stejný směr, pak práce W = Fs. V případě, že síla svírá se směrem posunutí úhel  , platí pro pr práci W = Fs cos , platí pro pr práci W = Fs cos  . Jednotkou práce je joule (J). . Jednotkou práce je joule (J).
Veličinu výkon P definujeme vztahem P = Wt-1, jde W je práce vykonaná rovnoměrně za dobu t. Jestliže se práce nekoná rovnoměrně, vyjadřuje uvedený vztah průměrný výkon. Při stálém výkonu platí pro práci W = Pt. Okamžitý výkon určíme pomocí vztahu P = Fv, kde F je velikost síly konající práci a v velikost rychlosti tělesa. Jedntkou výkonu je watt (W).
Těleso o hmotnosti m, které se pohybuje vzhledem k dané vztažné soustavě rychlostí v, má kinetickou energii Ek = 2mv-2. Jestliže těleso účinkem stálé síly F změní po dráze s svoji rychlost z hodnoty vy1y na hodnotu v2, změní se jeho kinetická energie o hodnotu 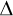 Ek a vykoná se práce Ek a vykoná se práce
W = Fs = 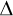 E k = E k2 - E k1 = 2mv 2-2 - 2mv 1-2.
Wztah W = Fs = 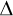 Ek platí obecně za předpokladu, že nepůsobí třecí síly a odpor prostředí. Ek platí obecně za předpokladu, že nepůsobí třecí síly a odpor prostředí.
Zvedneme-li v homogením tíhovém poli těleso o hmotnosti m do výšky h, vykonáme práci W = mgh a těleso má vzhledem k dané vztažné soustavě potenciální tíhovou energii i hodnotu 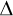 Ep = mgh. Jestliže zvedneme těleso o hmotnosti m z výšky hy1y d výšky h2, zvětší svoji potenciální energii o hodnotu Ep = mgh. Jestliže zvedneme těleso o hmotnosti m z výšky hy1y d výšky h2, zvětší svoji potenciální energii o hodnotu 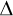 Ep a vykonáme práci Ep a vykonáme práci
W = 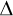 E p = E p2 - E p1 = mg(h 2 - h 1).
Vzhledem k vodorovné rovině, na které je potenciální tíhová energie nulová, má těleso ve výšce h nad touto rovinou potenciální tíhovou energii Ep = mgh.
Kinetickou a potenciální tíhovou energii tělesa souhrně nazýváme mechanická energie. Významným zákonem mechaniky je zákon zachování mechanické energie, podle něhož je celková změna mechanické energie izolované soustavy těles nulová, tj. 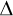 Ek + Ek + 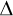 Ep =0, neboli celková mechanická energie izolované soustavy těles je stálá, tj. Ek + Ep = konst. Ep =0, neboli celková mechanická energie izolované soustavy těles je stálá, tj. Ek + Ep = konst.
U všech mechanických dějů probíhajících v izolované soustavě těles platí zákon zachování hmotnosti, zákon zachování hybnosti a v mnoha případech zákon zachování mechanické energie.
|



