Lesson
1: The Nature of a Sound Wave
Lesson 2: Sound Properties and Their Perception
Lesson 3: Behavior of Sound Waves
The Doppler Effect and Shock Waves
Reflection, Refraction, and Diffraction
Lesson 4: Resonance and Standing Waves
Fundamental Frequency and Harmonics
Lesson 5: Musical Instruments
Lesson 3: Behavior of Sound Waves
Boundary Behavior
As a sound wave travels through a medium, it will often reach the end of the medium and encounter an obstacle or perhaps another medium through which it could travel. When one medium ends, another medium begins; the interface of the two media is referred to as the boundary and the behavior of a wave at that boundary is described as its boundary behavior. The behavior of a wave (or pulse) upon reaching the end of a medium is referred to as boundary behavior. There are essentially four possible boundary behaviors by which a sound wave could behave: reflection (the bouncing off of the boundary), diffraction (the bending around the obstacle without crossing over the boundary), transmission (the crossing of the boundary into the new material or obstacle), and refraction (occurs along with transmission and is characterized by the subsequent change in speed and direction). In this part of Lesson 3, the focus will be upon the reflection behavior of sound waves. Later in Lesson 3, diffraction, transmission, and refraction will be discussed in more detail.
In Unit 10 of The Physics Classroom, the boundary behavior of a
pulse on a rope was discussed. 
In
that unit, it was mentioned that there are two types of
reflection for waves on ropes: fixed end reflection and free
end reflection. A pulse moving through a rope will
eventually reach its end. Upon reaching the end of the
medium, two things occur:
- A portion of the energy carried by the pulse is reflected and returns towards the left end of the rope. The disturbance which returns to the left is known as the reflected pulse.
- A portion of the energy carried by the pulse is transmitted into the new medium. If the rope is attached to a pole (as shown at the right), the pole will receive some of the energy and begin to vibrate. If the rope is not attached to a pole but rather resting on the ground, then a portion of the energy is transmitted into the air (the new medium), causing slight disturbances of the the air particles.
In the situation in which the rope is attached to the pole, fixed end reflection occurs. For the reflected pulse off the fixed end, there is one very notable observation: the reflected pulse is inverted. That is, if a crest is incident towards a fixed end, it will reflect and return as a trough. Similarly, if a trough is incident towards a fixed end, it will reflect and return as a crest.
In the situation in which the rope is not attached to the pole nor firmly attached to any other medium heavier than itself (such as another rope), free end reflection occurs. The reflected pulse off a free end is never inverted. That is, if a crest is incident towards a free end, it will reflect and return as a crest. Similarly, if a trough is incident towards a free end, it will reflect and return as a trough.
In each case (free and fixed end reflection, the amount of energy which becomes reflected is dependent upon the dissimilarity of the two medium. The more similar that the two medium on each side of the boundary are, the less reflection which occurs and the more transmission which occurs. Conversely, the less similar that the two medium on each side of the boundary are, the more reflection which occurs and the less transmission which occurs. So if a heavy rope is attached to a light rope (two very dissimilar medium), little transmission and mostly reflection occurs. And if a heavy rope is attached to another heavy rope (two very similar medium), little reflection and mostly transmission occurs.
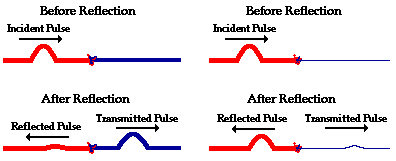
The more similar the medium, the more transmission which occurs.
These principles of free and fixed end reflection can be applied to sound waves. Though a sound wave does not consist of crests and troughs, they do consist of compressions and rarefactions. If a sound wave is traveling through a cylindrical tube, it will eventually come to the end of the tube. The end of the tube represents a boundary between the enclosed air in the tube and the expanse of air outside of the tube. Upon reaching the end of the tube, the sound wave will undergo partial reflection and partial transmission. That is, a portion of the energy carried by the sound wave will pass across the boundary and out of the tube (transmission) and a portion of the energy carried by the sound wave will reflect off the boundary, remain in the tube and travel in the opposite direction (reflection). If the end of the tube is "open" or uncovered such that the air at the end of the tube can freely vibrate when the sound wave reaches it, then the behavior at the boundary resembles free end reflection. There is no inversion of the disturbance when reflecting off the open end (uncovered end) of a cylindrical tube. That is, if a compression is incident towards an open-end, it will reflect and return as a compression. Similarly, if a rarefaction is incident towards an open end, it will reflect and return as a rarefaction. The opposite occurs if the end of the tube is "closed" or covered up. If the end of the tube is "closed" or covered, then the air at the end of the tube is fixed and cannot freely vibrate when the sound wave reaches it. In this case, the behavior at the boundary resembles fixed end reflection. There is inversion of the disturbance when reflecting off the closed end (covered end) of a cylindrical tube. That is, if a compression is incident towards an closed end, it will reflect and return as a rarefaction. Similarly, if a rarefaction is incident towards an closed end, it will reflect and return as a compression.
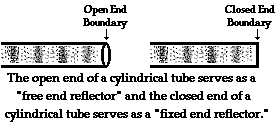
The behavior of sound waves at open ends and closed ends will become important Lesson 5 during the discussion of musical instruments. Many musical instruments operate as the result of sound waves traveling back and forth inside of "tubes" or air columns. These waves reflect at either a closed end or an open end of the air column; and the fact that inversion occurs at a closed end will have a huge impact on the numerical pattern of frequencies produced by such instruments.
The reflection of sound also becomes important to the design of concert halls and auditoriums. The acoustics of sound must be considered in the design of such buildings. The most important considerations include destructive interference and reverberations, both of which are the result of reflections of sound off the walls and ceilings. Designers attempt to reduce the severity of these problems by using building materials which reduce the amount of reflection and enhance the amount of transmission (or absorption) into the walls and ceilings. The most reflective materials are those which are smooth and hard; such materials are very dissimilar to air and thus reduce the amount of transmission and increase the amount of reflection. The best materials to use in the design of concert halls and auditoriums are those materials which are soft. For this reason, fiberglass and acoustic tile are used in such buildings rather than cement and brick.