Chapter 5 Special Models For Normal Data
In this Chapter, we deal with some important special cases of mixed models with Normal distribution. This will serve as illustrative examples of applying the EM-Algorithm (Theorem 4.4) from prior chapter. For certain models, it will also provide us some comparisons with existing results in the literature.
5.1 Univariate Models with Censored Data
For better understanding, we first demonstrate the algorithm when outcome is a scalar, i.e. k =1. Models for errors-in-variable have this form when there is no censoring. Scalar yi's are assumed independent given u, just as assumed before for vector yi. Specifically, let Σ1 = σe², and in most circumstances the parameters of interest for yi|u can be assumed as
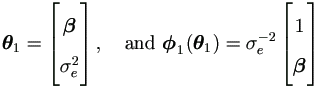 by equation (4.15).
by equation (4.15).
Even under this simplified setting, we can still model essentially all models that can be handled by the general setting above by adjusting Σ2, covariance structure of u.
By (4.19), the Jacobian matrices for θ1 is
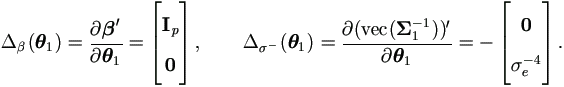
Now that  is a non-singular matrix,
we may drop this term from M-step (4.37), which becomes
is a non-singular matrix,
we may drop this term from M-step (4.37), which becomes
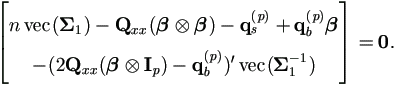
This can be further simplified as the solution of the following equation system.
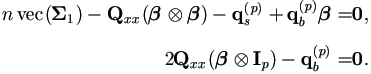
From the second equation above, we know that  Ip)
Ip)
 | (5.1) |
| (5.2) |
Since each Xi is a matrix of order k × p, we may
stack all Xi's for i =1, 2, ..., n to form a sample-wise
design matrix 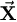 of order nk × p as
of order nk × p as

When k = 1, we have the following relationship
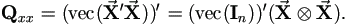
This is evident when treat 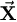 as a (block) vector with
each entry being one of the (row) vectors Xi. Then by
as a (block) vector with
each entry being one of the (row) vectors Xi. Then by

The last equality is due to that
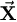 '
'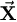 β is a column vector. Hence (5.1) leads to
β is a column vector. Hence (5.1) leads to 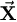 '
'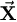 β
=½ q'b(p).
β
=½ q'b(p).
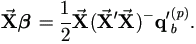 | (5.3) |
Since 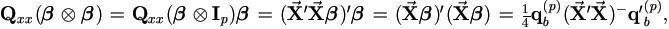 then by (5.2),
then by (5.2),
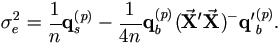 | (5.4) |
Therefore the M-step (4.37) can be replaced by these much simpler equations (5.3) and (5.4).
5.2 Mixed Models without Censored Data
We now present the algorithm for the mixed model for complete data with multivariate normal distribution. The algorithm is different from that is given by Dempster, Rubin and Tsutakawa (1981).
If all components of every yi are completely observed,
there is no need to calculate conditional expectations for
yi, so we can simplify the E-step substantially. Note that
now the observed data  = y. Therefore
we have
= y. Therefore
we have
Theorem 5.1. The EM-algorithm for mixed model with complete data from normal distribution can be defined as
| Step 0. | Start with values for parameters
 1(0) and 1(0) and
 2(0).
Set p = 0. 2(0).
Set p = 0.
|
||||
| Step 1. | (E-step) Calculate as given in (4.26) and (4.24),
|
||||
| Step 2. | (M-step) Determine
 (p+1)
by (p+1)
by
 1(p+1) = 1(p+1) =
 1(θ1(p+1))
as the solution of 1(θ1(p+1))
as the solution of
 2(p+1) = 2(p+1) =
 2(θ2(p+1))
as the solution of 2(θ2(p+1))
as the solution of
|
||||
| Step 3. | If converged, set  = =  (p+1); otherwise increase p by 1 and return to step 1. (p+1); otherwise increase p by 1 and return to step 1.
|
Special Case: A Univariate Mixed Model without Censored Data
Now we show that the algorithm above agrees with the EM-algorithm of section §2.2, where all yi are scalars (i.e. k = 1). Follow the same distributional assumptions and use notations in that section, we have
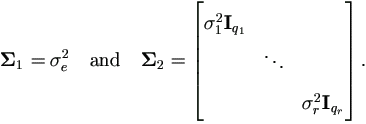
Then the parameters of interest are
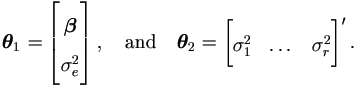
Also by equations (4.15) and (4.18), we have
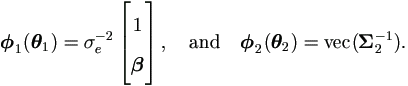
In order to be comparable to section §2.2, we stack all individual matrices as below to form the sample-wise matrices corresponding to y, X, Z, e of that section.
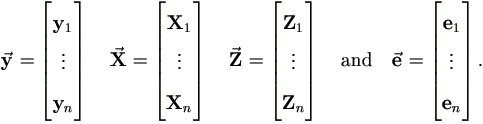
Then the model (4.1) can be written as

For Jacobian matrices, by (4.19),
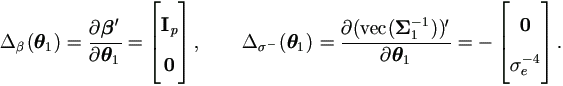
Note that now  is a non-singular matrix,
so we may drop this term from M-step (5.6), which becomes
is a non-singular matrix,
so we may drop this term from M-step (5.6), which becomes
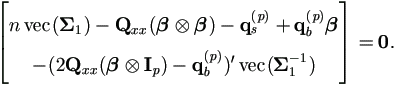 | (5.8) |
It is easy to verify that Qxx =
(vec(In))'(

 )
due to k =1. And by (5.5) we have
)
due to k =1. And by (5.5) we have
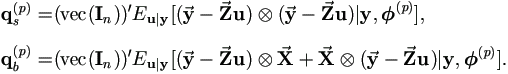
Then by above relationships and (A.4),
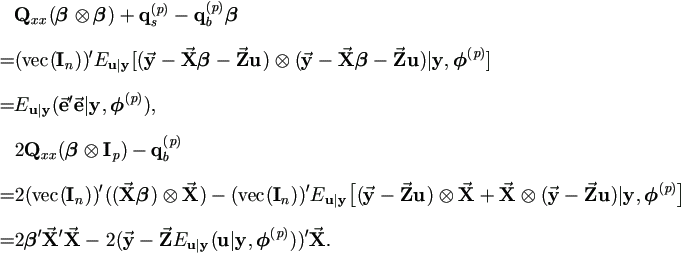 | (5.9) |
| (5.10) |
Therefore by (5.8) and (5.9),
n vec(Σ1) =  .
Since Σ1 = σe², we have
.
Since Σ1 = σe², we have
 /n.
/n.

These results agree with those in the EM-algorithm of section §2.2.
Let δij be the Kronecker symbol, then
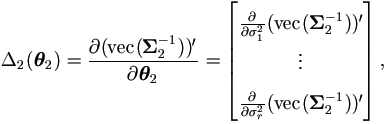 | (5.11) |

Now apply to equation (5.7), we get

Then for each j =1, 2, ..., r,

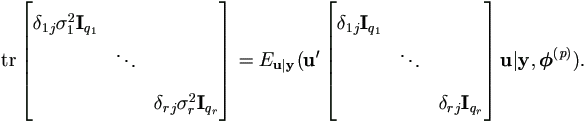
That is, qjσj²
= Eu|y u'juj|y,  (p)).
Therefore for j =1, 2, ..., r,
(p)).
Therefore for j =1, 2, ..., r,
σj² = Eu|y u'juj|y,  (p))/qj.
(p))/qj.
Pure random effect model is a special case of mixed models in equation (4.1), but without fixed effects. First, we derive the EM-algorithm based on Theorem 4.4 for this special case, and then compare the results with that from Pettitt's approach (Pettitt, 1986) as outlined in section §1.4.2.
Since X = 0, the model becomes y = Zu + e. Theorem 4.4 becomes much simpler as many terms go to 0. Since qb(p) = Qxx = 0, we have
Lemma 5.1.
The M-step for pure random effects model from normal distribution is
as follows. Determine
 (p+1)
by
(p+1)
by
 1(p+1) =
1(p+1) =
 1(θ1(p+1))
as the solution of
1(θ1(p+1))
as the solution of
and  2(p+1) =
2(p+1) =
 2(θ2(p+1))
as the solution of
2(θ2(p+1))
as the solution of
Lemma 5.2.

Proof. Note that ei = yi - Ziu and by (4.26),
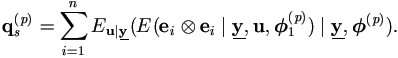
Then the desired result will be obtained by applying (A.6).
Lemma 5.3.
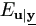 (uu'|
(uu'|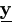 ,
,  (p))).
(p))).
Proof.
By definition (4.24), 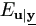 (u
(u u|
u|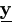 ,
,  (p)).
(p)). u = vec(uu'),
u = vec(uu'),
Theorem 5.2. EM-algorithm for pure random effects model from normal distribution is defined below. Note that Σ1 = Σ1(θ1) and Σ2 = Σ2(θ2).
| Step 0. | Start with values for parameters
 1(0) and 1(0) and
 2(0).
Set p = 0. 2(0).
Set p = 0.
|
||||
| Step 1. | (E-step) Calculate 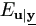 (eie'i| (eie'i|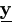 , ,  (p)) and (p)) and 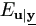 (uu'| (uu'|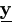 , ,  (p)) as given above. (p)) as given above.
|
||||
| Step 2. | (M-step) Determine
 (p+1)
by (p+1)
by
 1(p+1) = 1(p+1) =
 1(θ1(p+1))
as the solution of 1(θ1(p+1))
as the solution of
 2(p+1) = 2(p+1) =
 2(θ2(p+1))
as the solution of 2(θ2(p+1))
as the solution of
|
||||
| Step 3. | If converged, set 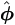 = =  (p+1); otherwise increase p by 1 and return to step 1. (p+1); otherwise increase p by 1 and return to step 1.
|
5.3.2 Special Case: Pettitt's Model
Now compare the results based on Theorem 5.2 and that from section 2 of Pettitt's paper (1986) as outlined in section §1.4.2 for the usual random effects models.
Since Σ1=σ²Ik, let
θ1=σ², then
Σ1(θ1)=θ1Ik. From equation (4.15),
we have  1(θ1)
1(θ1) 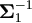 )
)
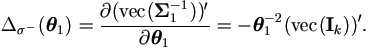
Now equation (5.12) becomes

By equation (A.2), it becomes

Since tr(eie'i) = e'iei, then n tr(Σ1) = 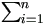
 . Since tr(Σ1) = kσ², and let
. Since tr(Σ1) = kσ², and let
 .
.
This agrees with Pettitt's result as nk here is equal to qk+1 in Pettitt's paper.
In order to compare results for other random components, let us map Pettitt's model into our framework. To avoid ambiguity over notations, here we use m to denote k in that paper. Now we have

and by equation (4.18) we have
 2(θ2)=vec(
2(θ2)=vec( ), where
), where
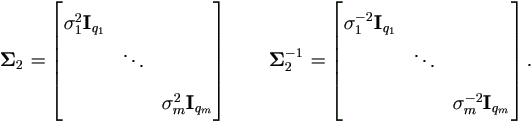
Let δij be the Kronecker symbol, then for Δ2,
 | (5.14) |

Apply to equation (5.13), we get

Then for each j =1, 2, ..., m,
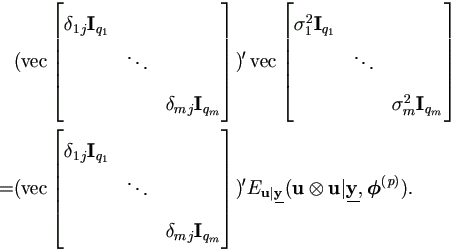
By (A.2) and (A.4) in the Appendix,
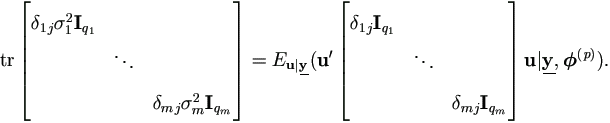
Therefore, for i =1, 2, ..., m,
qiσi² = 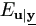 (x'ixi|
(x'ixi|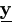 ,
,  (p)).
(p)).
These results again agree with those from Pettitt's paper.
All results agree on that the E-step must be carried out for the
expectation of x'ixi or e'e with
respect to the conditional distribution of x or
e given 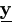 . The core calculation
involved is in fact about the conditional expectations for
yi and yi
. The core calculation
involved is in fact about the conditional expectations for
yi and yi  yi over incomplete
observations as given in equations (4.30) and
((4.31). They are equivalent to the formulae given in
section 2.2 in Pettitt's paper. However, the calculation is very
complicated in general. The method provided by Pettitt in section 3
circumvents this difficulty for a simple type of model. In fact it is
only easily available when the structure of variance-covariance matrix
is simple. In general, we must use numerical methods to approximate
multi-dimensional integrals.
yi over incomplete
observations as given in equations (4.30) and
((4.31). They are equivalent to the formulae given in
section 2.2 in Pettitt's paper. However, the calculation is very
complicated in general. The method provided by Pettitt in section 3
circumvents this difficulty for a simple type of model. In fact it is
only easily available when the structure of variance-covariance matrix
is simple. In general, we must use numerical methods to approximate
multi-dimensional integrals.
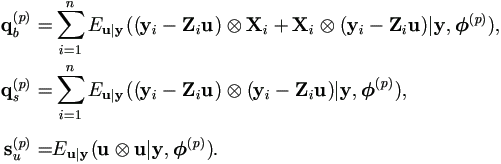
 .
. . Hence
. Hence
