บทที่ 2 เอกสารอ้างอิง

เอกสารอ้างอิง

ในโครงงานฉบับนี้ เราต้องอาศัยความรู้หลากหลายเรื่อง ดังนี้

2.1 Fractals

2.2 การใช้วิธีสังเกตรูปที่คล้ายกัน (Self–Similarity) ในการหาความยาวและพี้นที่เกลียว

2.3 ซอฟต์แวร์คอมพิวเตอร์ Geometer’s Sketchpad (GSP)

ความรู้ดังกล่าวมีรายละเอียดดังต่อไปนี้

2.1 Fractals

Mandelbrot มักจะเสนอลักษณะใหม่ ๆ ของ Fractals แต่ข้อเสนอนั้นบางคนตั้งข้อสังเกตว่าเกิดจากวิธีการทางคณิตศาสตร์ของนักคณิตศาสตร์สมัยโบราณ เช่น Georg Cantor (1872) Helge von Koch (1904) หรือ Waclaw Sierpinski (1916)

นักคณิตศาสตร์เป็นผู้สร้างกฎเพื่อให้เกิดแนวคิดใหม่ ๆ แต่ในเวลาเดียวกันก็จะคอยสังเกตสิ่งต่างๆจากธรรมชาติว่ามีอะไรที่พวกเขารู้ เช่น Contor Set , Koch Snowflake , Peano Curve หรือ Sierpinski Gesket and Carpet ซึ่งข้อสรุปจากการสังเกตมักจะมีลักษณะพิเศษแทบทั้งสิ้น เช่นเดียวกับ Fractals เกิดขึ้นจากความพยายามที่จะสำรวจในสิ่งใหม่ ๆ ของนักคณิตศาสตร์ ภายใต้ขอบเขตของความรู้ที่มีอยู่

Mandelbrot พยายามจะแสดงลักษณะของ Fractals ในทางคณิตศาสตร์ซึ่งรูปร่างลักษณะเหล่านั้นสามารถพบได้ตามธรรมชาติ เขาพยายามนำมาจัดระเบียบ พัฒนาปรับปรุง และใช้ภาษาแสดงชื่อเรียกตามลักษณะเหล่านั้น ดังนั้น Mandelbrot จึงได้ชื่อว่าเป็นบิดาแห่ง Fractals

Fractals ประกอบด้วยรูปแบบ 4 รูปแบบ คือ

The Contor Set
The Sierpinski Gasket and Carpet
The Pascal Triangle
The Koch Snowflake

ซึ่งแต่ละรูปแบบก็มีลักษณะแตกต่างกันออกไป ดังนี้

รูปที่ 2 The Contor Set

รูปที่ 3.1 The Sierpinski Gasket

รูปที่ 3.2 The Sierpinski Carpet

รูปที่ 4 The Pascal’s Triangle

รูปที่ 5 The Koch Snowfale

2.1.1 The Koch Snowflake

รูปที่ 6 แสดงให้เห็นถึงการสร้างรูป Koch Curve

ในปี 1904 Helge von Koch นักคณิตศาสตร์ชาวสวีเด็น เป็นผู้แนะนำให้รู้จักว่าอะไรคือ “ Koch Curve” จากรูปที่ 6 จะแสดงให้เห็นถึงการสร้างรูป Koch Curve

Koch Snowflake เกิดจากการนำ Koch Curve 3 ด้านซึ่งเท่ากันมาประกอบกัน ดังรูปที่ 7

รูปที่ 7 The Koch Snowflake

รูปที่ 8 Circle , Square and Koch Snowflake

2.2 การใช้วิธีสังเกตรูปที่คล้ายกัน (Self-Similarity) ในการหาความยาวและพื้นที่เกลียว

2.2.1 การใช้วิธีสังเกตรูปที่คล้ายกัน(Self-Similarity) ในการหาความยาวเกลียว

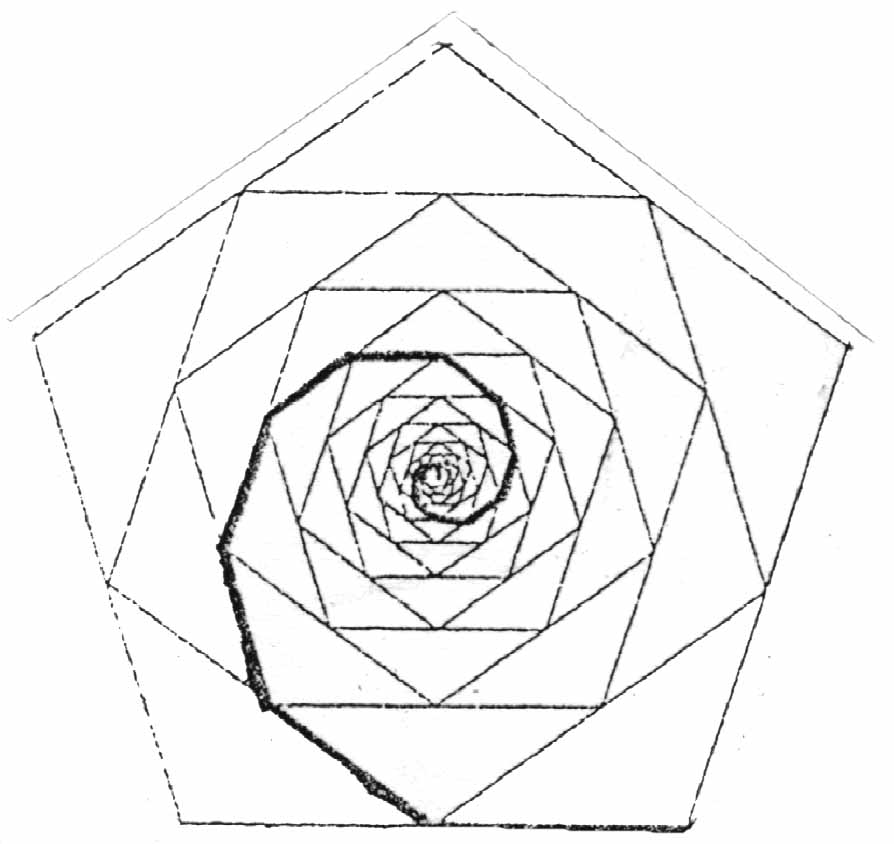
รูปที่ 9 เกลียวที่เกิดภายในรูปห้าเหลี่ยมด้านเท่า

เราต้องการหาความยาวเกลียวของรูปทั่ว ๆ ไป คือเกิดจากรูป n-เหลี่ยมด้านเท่า ซึ่งเชื่อมกึ่งกลางของแต่ละด้านเกิดเป็นรูป n-เหลี่ยมด้านเท่าขึ้นภายใน ดังรูปที่ 9 ทำซ้ำเช่นนี้ไปเรื่อย ๆ จะได้จำนวนรูป n-เหลี่ยมด้านเท่าซ้อนกันอยู่ภายในเป็นจำนวนอนันต์รูป ครึ่งหนึ่งของด้านจะถูกลากเชื่อมต่อกันเกิดเป็นเกลียวขึ้น ตัวอย่างเช่นรูปห้าเหลี่ยมด้านเท่าในรูปที่ 9

จากความรู้ที่ว่า มุมภายนอกของรูป n-เหลี่ยมด้านเท่าจะมีขนาดของมุม คือ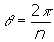 เมื่อ n แทนจำนวนเหลี่ยมทั้งหมด

สมมุติให้ ความยาวแต่ละด้านของรูป n-เหลี่ยมด้านเท่าเป็น L ลากเส้นเชื่อมระหว่างจุดกึ่งกลางของด้านเพื่อสร้าง รูป n-เหลี่ยมด้านเท่าขึ้นภายใน เส้นที่ลากขึ้นใหม่นี้จะทำให้เกิดรูปสามเหลี่ยมหน้าจั่วที่มีความยาวด้านสองด้านคือ 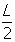และมุมที่ฐานจะมีขนาดเท่ากับครึ่งหนึ่งของมุมภายนอก คือ 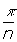จากรูปที่ 10 เราสามารถคำนวณหาความยาวด้านของรูป n-เหลี่ยมด้านเท่าภายใน l ได้

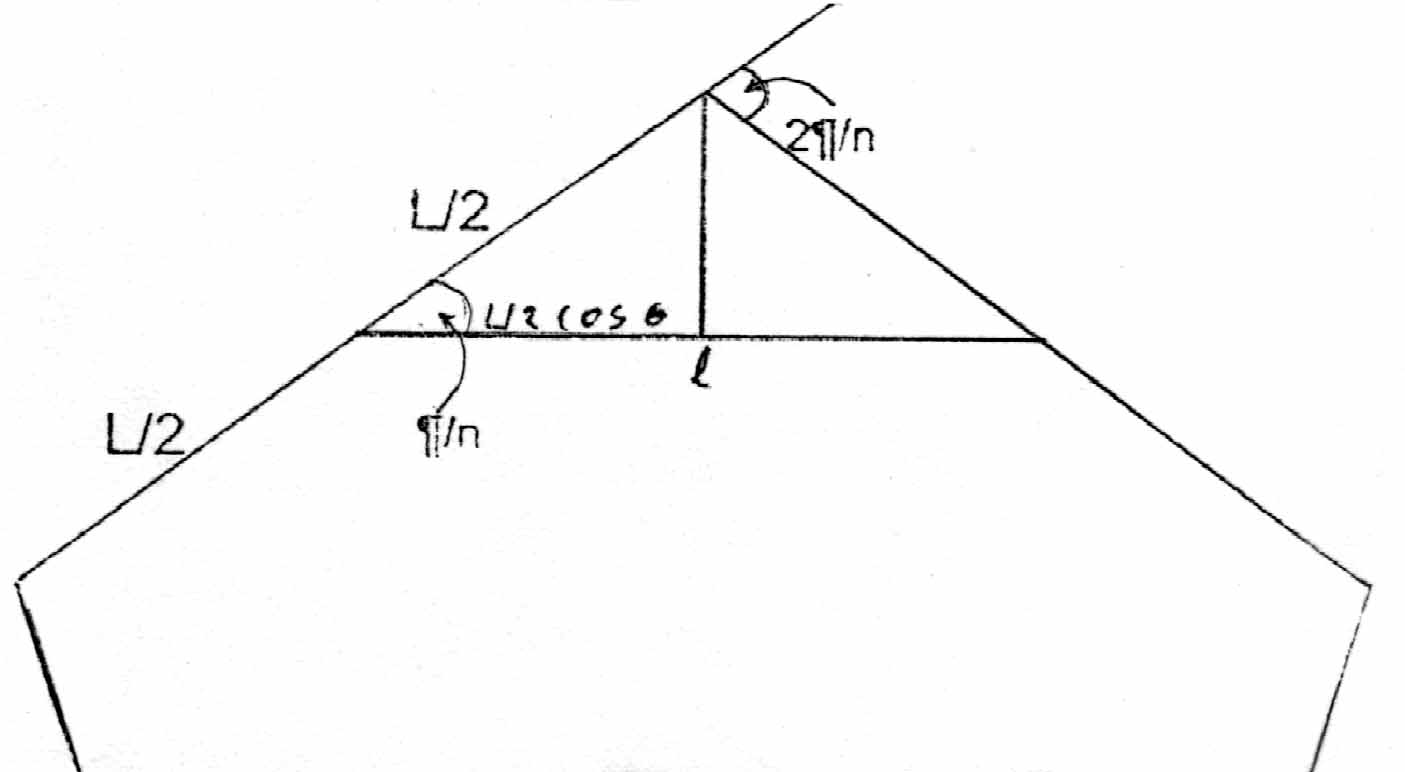
รูปที่ 10 รูป n-เหลี่ยมด้านเท่าที่แสดงถึงมุมภายนอก และมุมที่ฐานของรูปสามเหลี่ยมหน้าจั่ว

การหาความยาวเกลียว

เนื่องจากความยาวด้านของ รูป n – เหลี่ยมด้านเท่า ที่บรรจุอยู่ภายในเกิดจาก

cos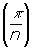 คูณกับความยาวด้านของ รูปn-เหลี่ยมด้านเท่ารูปใหญ่ ดังนั้น scaling factor ระหว่าง รูป n-เหลี่ยมด้านเท่าภายในกับ รูป n-เหลี่ยมด้านเท่าภายนอก คือ p = cos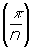

ให้ L แทนความยาวแต่ละด้านของรูป n-เหลี่ยมด้านเท่า

S แทนความยาวเกลียวของรูป n-เหลี่ยมด้านเท่า

s แทนความยาวเกลียวของรูป n-เหลี่ยมด้านเท่าที่ลบรูป n-เหลี่ยมด้านเท่าด้านนอกสุดออก

จะได้ความสัมพันธ์ระหว่างรูปที่คล้ายกัน คือ s = cos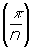S ----------À

จะได้ความสัมพันธ์ของความยาวเกลียว คือ S = 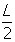+ s ----------Á

แทนค่า À ใน Áจะได้

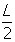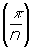S = + cosS

S - co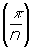sS =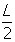

=

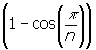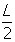
S =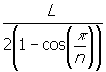

2.2.2 การใช้วิธีสังเกตรูปที่คล้ายกัน(Self-Similarity) ในการหาพื้นที่เกลียว

ถ้ารูปสองรูปคล้ายกันโดยมี scaling factor (p) แล้ว พื้นที่ของรูปทั้งสองจะสัมพันธ์ด้วยอัตราส่วน p²

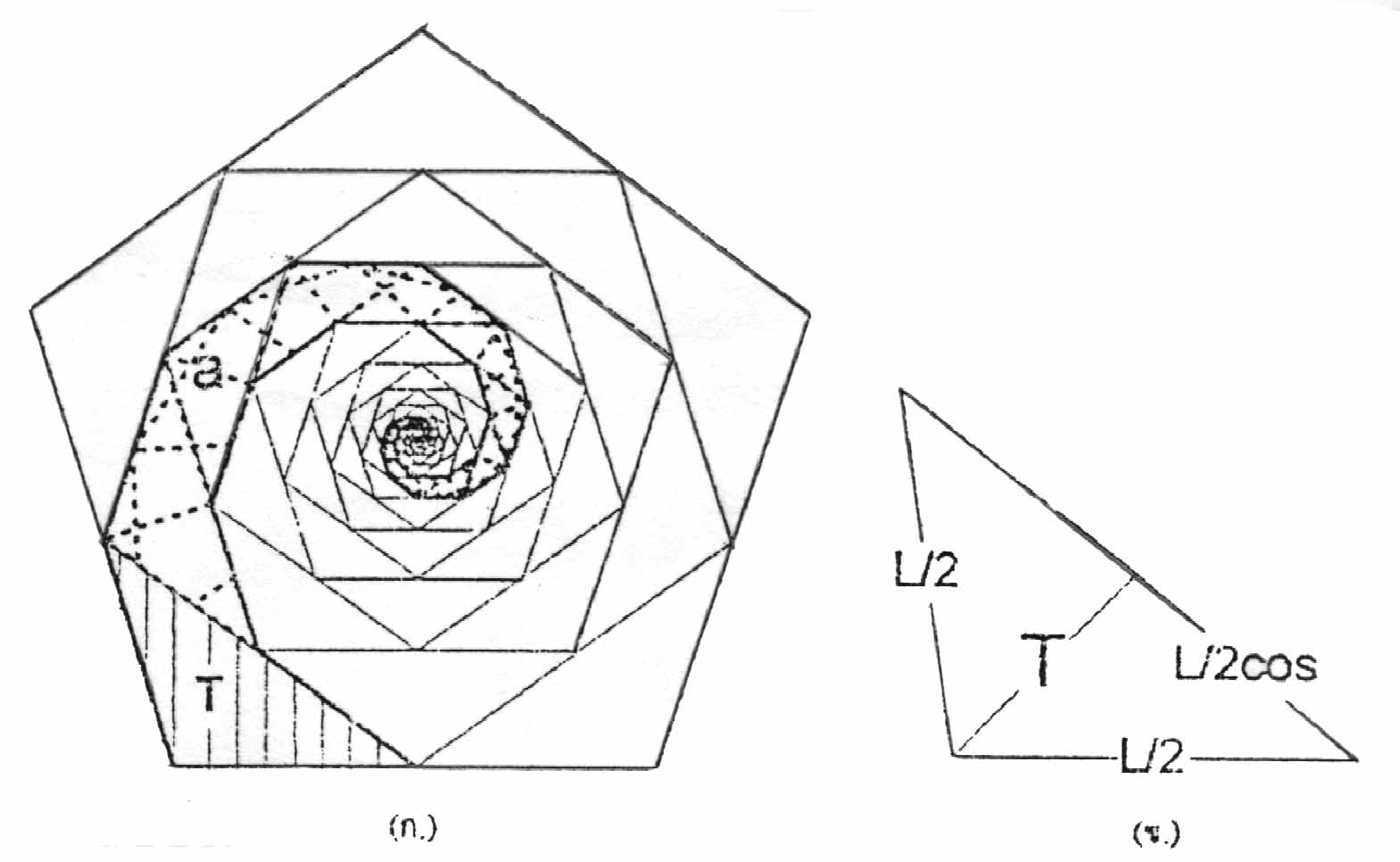
รูปที่ 11 (ก.) พื้นที่เกลียวที่เกิดภายในรูปห้าเหลี่ยมด้านเท่า
(ข.)พื้นที่รูปสามเหลี่ยมที่ถูกลบออกจากการลบรูปห้าเหลี่ยมด้านเท่า ด้านนอกของรูป (ก.)

การหาพื้นที่เกลียว

เมื่อพิจารณารูป n-เหลี่ยมด้านเท่าที่บรรจุอยู่ภายใน แรเงามุมหนึ่งของรูป ดังรูปที่ 11 (ก.) แทนที่จะระบายแค่หนึ่งเส้น(เส้นทึบในรูปที่ 9)

ให้ A แทนพื้นที่เกลียวของรูป n-เหลี่ยมด้านเท่า

a แทนพื้นที่เกลียวที่ลบรูป n-เหลี่ยมด้านเท่าด้านนอกออก

T แทนพื้นที่รูปสามเหลี่ยมที่ถูกตัดออก

scaling factor (p) คือ cos ²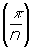

จะได้ความสัมพันธ์ระหว่างรูปที่คล้ายกัน คือ a = Acos ²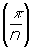 ----------À

เราสามารถคำนวณหาความยาวของแต่ละด้านของรูปสามเหลี่ยม T ได้ โดยอาศัยทฤษฎี Phytagorian ได้พื้นที่ของรูปสามเหลี่ยม T คือ

T =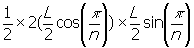

T = 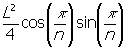----------Á

เนื่องจาก A = T + a ----------Â

แทนค่า T และ a จากสมการ À และ Á

A = 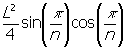+ Acos ²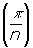

A - Acos ²=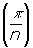

=

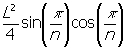
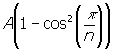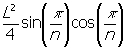
A = 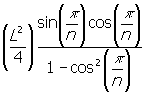----------Ã

จาก 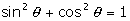และ 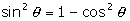แทนค่าใน Ã

A =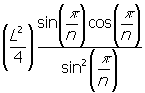

A =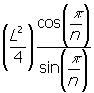

A =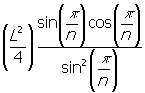

2.3 Geometer’s Sktchpad (GSP)

GSP ได้ถูกพัฒนามาจากส่วนหนึ่งของโครงการพัฒนาเรขาคณิตที่มองเห็นได้ (Visual Geometry Project) ของมูลนิธิวิทยาศาสตร์แห่งชาติ สหรัฐอเมริกา

ในปี 1987 นิโคลัส แจคคิว (Nicholas Jackiw) ร่วมกับโครงการพัฒนาเรขาคณิตที่มองเห็นได้ ได้พัฒนา GSP นี้จนสามารถนำมาใช้กับเครื่องแมคอินทอช (Macintosh) ได้สำเร็จ

ในปี 1990 นิโคลัส เข้ามาทำงานร่วมกับ สำนักพิมพ์ คีย์ เคอร์ริ-คิวลัม (Key Curriculum) และได้ผลิตซอฟต์แวร์ตัวแรกขึ้น เป็นรุ่นเบต้า (Beta Version)

การเปิดตัวของ GSP ทำให้เกิดการพัฒนาอย่างรวดเร็ว ในปี 1991 GSP นี้ เริ่มใช้กันอย่างแพร่หลายมากขึ้นในหมู่ครู อาจารย์ และนักเรียนที่สนใจ

ในปี 1993 GSP ได้มีการปรับปรุงรูปแบบการทำงานอีกครั้ง จนสามารถนำมาใช้กับระบบปฏิบัติการวินโดส์ (Window) ได้เป็นผลสำเร็จ GSP มีรุ่นสาธิต (Demo Version) ซึ่งสามารถโหลด (Load) ได้ทางอินเตอร์เน็ต สำหรับผู้ที่สนใจใช้ในการศึกษา โดย GSP รุ่นสาธิตมีประสิทธิภาพในการปฏิบัติงานใกล้เคียงกับ GSP รุ่นเต็ม (Full Version) เพียงไม่มีคู่มือประกอบการใช้งาน และไม่สามารถบันทึกเก็บไว้ได้เท่านั้น

GSP ถูกสร้างขึ้นเพื่อใช้สำหรับการเรียนในระดับมัธยมศึกษา และในปัจจุบันโปรแกรมนี้ก็ใช้กันอย่างแพร่หลายในนักเรียนระดับมัธยมศึกษาของสหรัฐอเมริกา สำหรับในประเทศไทยนั้น การนำGSPมาใช้ในการสอนของโรงเรียนยังไม่แพร่หลายนัก

2.3.1 การใช้งานเบื้องต้น

สำหรับ GSP ที่ใช้นั้นเป็นรุ่นสาธิตซึ่งการใช้งาน GSP รุ่นสาธิตมีขั้นตอนในการปฏิบัติตามลำดับ ดังนี้

นำโปรแกรม GSP รุ่นสาธิตมา copy ลงในคอมพิวเตอร์ โดยระบบของ คอมพิวเตอร์ต้องเป็นระบบปฏิบัติการ Microsoft Windows 3.1 หรือ Microsoft Windows 95 หรือสูงกว่า

แรม(Ram) อย่างน้อย 4 เมกาไบต์

เข้าไปที่โปรแกรม GSP หน้าจอจะปรากฎ ดังรูปที่ 12

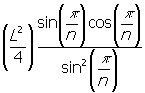
รูปที่ 12 หน้าจอของ GSP