





| สรุปและอภิปราย
สรุป
- การนำ GSP มาช่วยในการสร้าง Koch Snowflake นั้นทำให้เราสามารถสร้างKoch Snowflake ได้รวดเร็วยิ่งขึ้น ทั้งยังสามารถกำหนด Loop กำหนดขนาดของรูปตามที่ต้องการได้ และในการใช้ GSP สร้าง Koch Snowflake นั้นเราก็ยังคงยึดหลักเดียวกันกับการสร้าง Koch Snowflake ปกติ
- การหาพื้นที่ของ Koch Snowflake ด้วยสูตร เราสามารถหาได้ด้วยสูตร ดังนี้
 เมื่ออัตราส่วน p = q เมื่ออัตราส่วน p = q
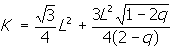 เมื่ออัตราส่วน p ¹q เมื่ออัตราส่วน p ¹q
- การหาพื้นที่ของ Koch Snowflake ด้วย GSP นั้น มีขอจำกัด คือ Koch Snowflake เป็นรูปที่สร้างต่อเนื่องไปอย่างไม่มีที่สิ้นสุด แต่การหาพื้นที่ด้วย GSP เราต้องกำหนดขอบเขตสิ้นสุดในการหาพื้นที่ เพราะฉะนั้นค่าพื้นที่ของ Koch Snowflake ที่ได้ จึงเป็นแค่เพียงค่าที่ใกล้เคียงเท่านั้น และในการหาพื้นที่ Koch Snowflake ด้วย GSP นั้น เราต้องหาพื้นที่รูปสามเหลี่ยมแต่ละรูป แล้วนำมาบวกกัน
- จำนวนรูปสามเหลี่ยมทั้งหมดที่นำมาประกอบเป็น Koch Snowflake ทั้งหมดคือ 1+3(4)n-1 เมื่อ n = 1 , 2 , 3 ,
ข้อเสนอแนะ
- การสร้างและการหาพื้นที่ในโครงงานนี้ จะเน้นการศึกษาเฉพาะ Fractals รูปKoch Snowflake ดังนั้น ควรนำความรู้นี้ไปเป็นแนวทางในการสร้างและหาพื้นที่ของ Fractals รูปอื่น ๆ ต่อไป
- ควรนำความรู้เกี่ยวกับการใช้ GSP นี้ไปประยุกต์เพื่อใช้ในการศึกษาเนื้อหาเกี่ยวกับเรื่องเรขาคณิตต่อไป
- ควรนำความรู้ที่ได้ไปใช้ในการหาพื้นที่หรืออาณาบริเวณใดจริง ๆ
บรรณานุกรม
Dan Bennett , Exploring Geometry with The Geometry : Dynamic Geometry for
the 21st Century , Key Curriculum press . California , 1996.
Heinz-Otto Peitgen , Hartmut Jürgens , Dietmar Saupe , Chaos and Fractals : New
Frontiers of Science , Hamilton Printing Co. , New York , 1992.
Sandefur , James T , Discrete Dynamical Modeling , Oxford University Press , New York , 1993.
www.keypress.com
|

