|
ชื่อโครงงาน
| |
Koch Snowflake & GSP
|
 |
ผู้ทำโครงงาน
| |
นางสาวดวงกมล เบ้าวัน
|
 |
| |
นักเรียนในโครงการพัฒนาและส่งเสริมผู้มีความสามารถพิเศษทางวิทยาศาสตร์และเทคโนโลยี (พสวท.)
|
 |
| |
ชั้นมัธยมศึกษาปีที่ 6 ปีการศึกษา 2543 โรงเรียนสามเสนวิทยาลัย |
 |
ที่ปรึกษาโครงงาน
| |
ศ.ดร.ยงค์วิมล เลณบุรี มหาวิทยาลัยมหิดล |
 |
| |
อาจารย์ ดร.วรรณวิภา สุทธเกียรติ โรงเรียนสามเสนวิทยาลัย |
 |
สาขาวิชา
| |
คณิตศาสตร์ |
|
อื่น ๆ
| |
นำเสนอในงานประชุมวิชาการครั้งที่ 15 โรงเรียนนายร้อย จปร. จังหวัดนครนายก |
|
บทคัดย่อ
พื้นที่หรืออาณาบริเวณใด ๆ บนโลกไม่ได้เป็นรูปที่มีสูตรในการหาพื้นที่ได้อย่างแน่นอน
ดังนั้นเราจึงต้องสร้างรูปเพื่อใช้เป็นต้นแบบขึ้น โดยในโครงงานนี้ได้ใช้ Koch Snowflake
เป็นรูปต้นแบบ แต่ในการสร้างและการหาพื้นที่ของ Koch Snowflake
แต่ละครั้งก็ยุ่งยากและต้องใช้เวลามาก ดังนั้นจึงได้มีการนำเครื่องมือเข้ามาช่วยในการสร้างและหาพื้นที่ของ
Koch Snowflake โดยเครื่องมือดังกล่าวคือ ซอฟต์แวร์คอมพิวเตอร์
Geometer's Sketchpad (GSP)
จากการศึกษาพบว่า ในการสร้าง Koch Snowflake นั้น
เราต้องแบ่งส่วนของเส้นตรงออกเป็น 3 ส่วนด้วยอัตราส่วน p : q : p และ 2p > q
บนส่วน q สร้างรูปสามเหลี่ยมหน้าจั่ว โดยให้มีด้านที่ยาวเท่ากัน มีความยาวเป็น p
ลบส่วนฐาน(q)ออก ทำเช่นนี้ไปเรื่อยๆ จะได้ Koch Curve 1 ด้าน นำ Koch Curve 3
ด้านมาและกอบกันจะได้ Koch Snowflake 1 รูป
การนำ GSP มาช่วยในการสร้างรูปนั้นมีความสะดวก รวดเร็วและได้รูปที่สวยงามกว่า
ซึ่งหลักการสร้าง Koch Snowflake ก็ใช้หลักการเดียวกัน
การหาพื้นที่ของ Koch Snowflake เราต้องนำวิธี Self-Similarity เข้ามาช่วยในการคิด
และสูตรที่จะใช้ในการคำนวณก็คือ
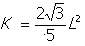 เมื่ออัตราส่วน p = q เมื่ออัตราส่วน p = q
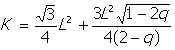 เมื่ออัตราส่วน p ≠ q เมื่ออัตราส่วน p ≠ q
เมื่อ L แทนความยาวของด้านของรูปสามเหลี่ยมด้านเท่ารูปใหญ่
q แทนอัตราส่วนของด้าน
การหาพื้นที่ของ Koch Snowflake ด้วย GSP นั้น เราต้องกำหนดขอบเขตของรูปที่เราต้องการจะหาพื้นที่
แต่ Koch Snowflake เป็นรูปที่สร้างต่อเนื่องไปโดยไม่มีที่สิ้นสุด ดังนั้นค่าที่คำนวณได้จากสูตร
และค่าที่คำนวณได้จาก GSP จึงมีค่าไม่เท่ากัน แต่จะมีค่าใกล้เคียงกันมาก
เขียนสมุดเยี่ยม
อ่านสมุดเยี่ยม

Since 17/1/2001
By Duangkamon B.
DPST'15 Samsen Wittayalai
|






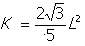 เมื่ออัตราส่วน p = q
เมื่ออัตราส่วน p = q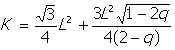 เมื่ออัตราส่วน p ≠ q
เมื่ออัตราส่วน p ≠ q
