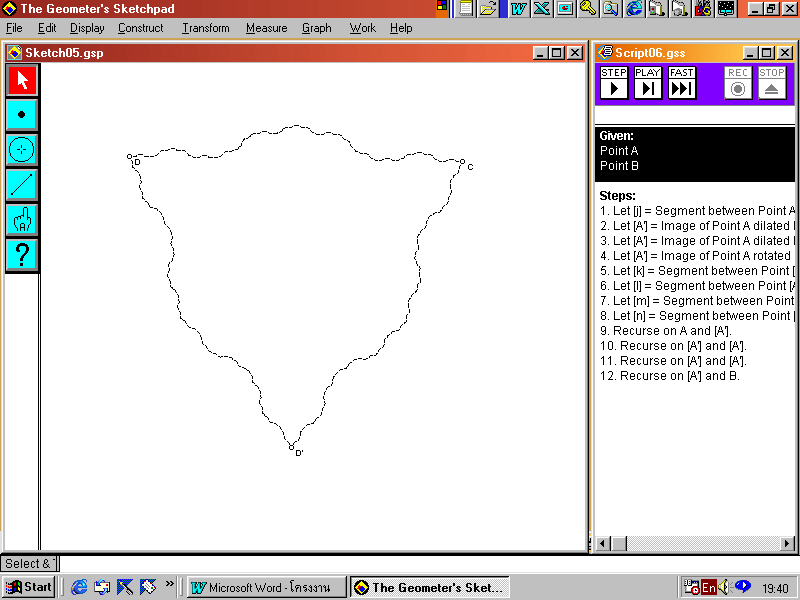
ในการคำนวณพื้นที่ x จะแบ่งออกเป็น 2 ส่วน ส่วนแรกคือ การคำนวณพื้นที่ของรูปสามเหลี่ยมหน้าจั่ว ซึ่งให้รูปสามเหลี่ยมหน้าจั่วมีพื้นที่เป็น T จะได้ว่า
ส่วนที่สอง คือการหาพื้นที่อีกสี่ส่วนที่อยู่รอบรูปสามเหลี่ยมหน้าจั่ว ให้พื้นที่ส่วนหนึ่งมีค่าเป็น y ดังนั้นเราจะได้
x = T + 4y ----------l
และพื้นที่ส่วน y นี้เป็นพื้นที่ซึ่งคล้ายกับพื้นที่ระหว่างด้านของรูปสามเหลี่ยมกับ Koch Curve โดยมี Scaling factor เป็น p ดังนั้น
y = p2x
แทนค่า y ลงในสมการ lจะได้
x = 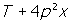
x = 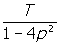
แต่ 1-4p2 = (1-2p)(1+2p) = q(2-q) ดังนั้นจะได้
x = 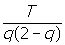 แทนค่า T จาก k
แทนค่า T จาก k
x = 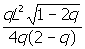
x = 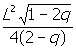 แทนค่าลงใน j
แทนค่าลงใน j
ดังนั้นพื้นที่ของ Koch Snowflake ที่มีรูปทรงที่เปลี่ยนไปคือ
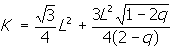
4.3 การสร้างรูป Koch Snowflake โดยใช้โปรแกรม GSP
ข้อตกลงเกี่ยวกับคำศัพท์บางคำ
- คลิก เป็นการกดปุ่มซ้ายของเมาส์ 1 ครั้ง แล้วปล่อยทันที
- คลิกขวา เป็นการกดปุ่มขวาของเมาส์ 1 ครั้ง แล้วปล่อยทันที
- ดับเบิลคลิก เป็นการกดปุ่มซ้ายของเมาส์ 2 ครั้ง ติดต่อกันอย่างรวดเร็ว
- Pointer เป็นตัวชี้ตำแหน่งบนวินโดวส์ ซึ่งเคลื่อนที่ตามการเคลื่อนที่ของเมาส์
จากการศึกษาการทำงานของซอฟต์แวร์ GSP สามารถนำมาใช้ในการสร้างรูป Koch Snowflake ได้ดังนี้
1. เข้าสู่โปรแกรม GSP เปิดไฟล์ New Sketch และ New Script
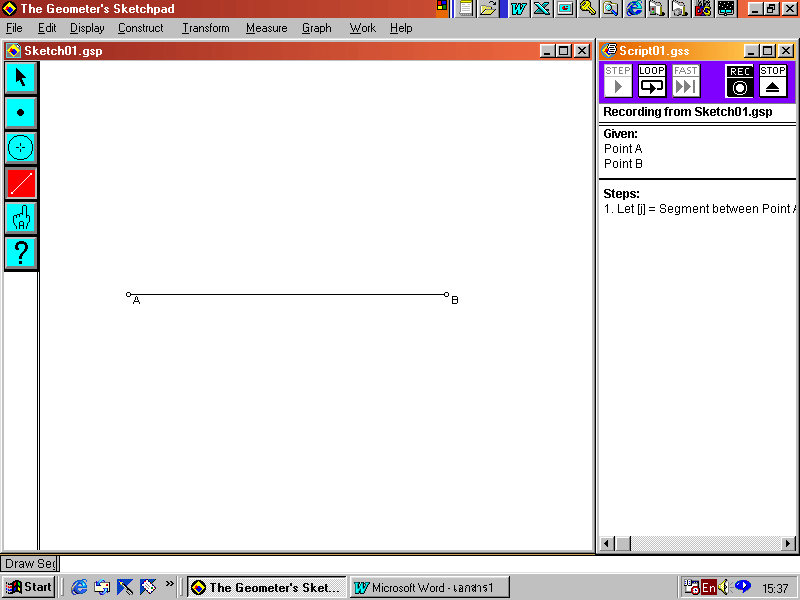
2. คลิก Rec ที่หน้าต่าง Script
3. ที่หน้าต่าง Sketch คลิกที่ Straightedge tools ลาก Pointer ไปที่ Sketch Plane แล้วคลิกค้างเพื่อสร้างส่วนของเส้นตรง AB
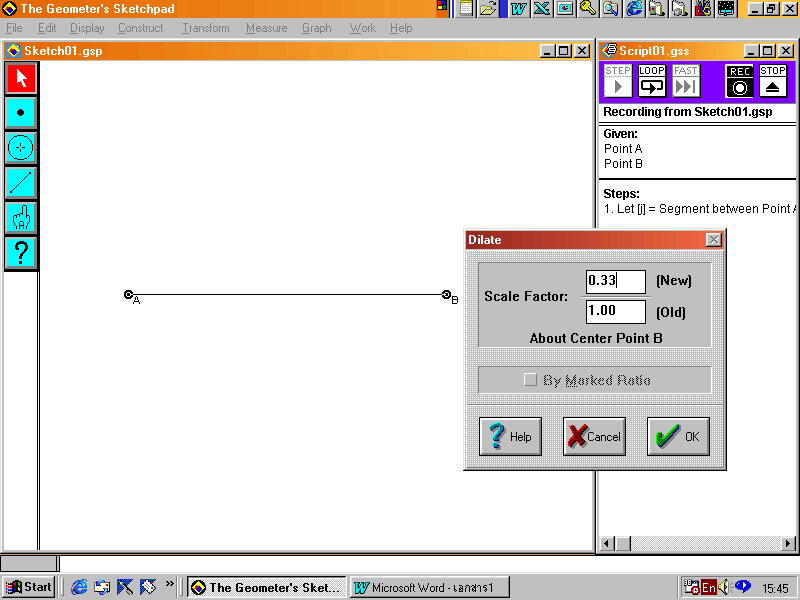
4. คลิกที่ Selection Arrow tools แล้วเลือกจุดปลายทั้งสองของส่วนของเส้นตรง AB โดยกด Shift ค้างไว้พร้อมกับคลิกที่จุดทั้งสอง ดับเบิลคลิกที่จุด B
5.คลิกขวา เลือก Transform แล้วเข้าไปที่ Dilate กำหนดค่า Scale Factor (New) เป็น 1 (Old) เป็น 3 คลิก OK
6. ทำซ้ำข้อ 4 และ 5 แต่กำหนดค่า Scale Factor (New)เป็น 2
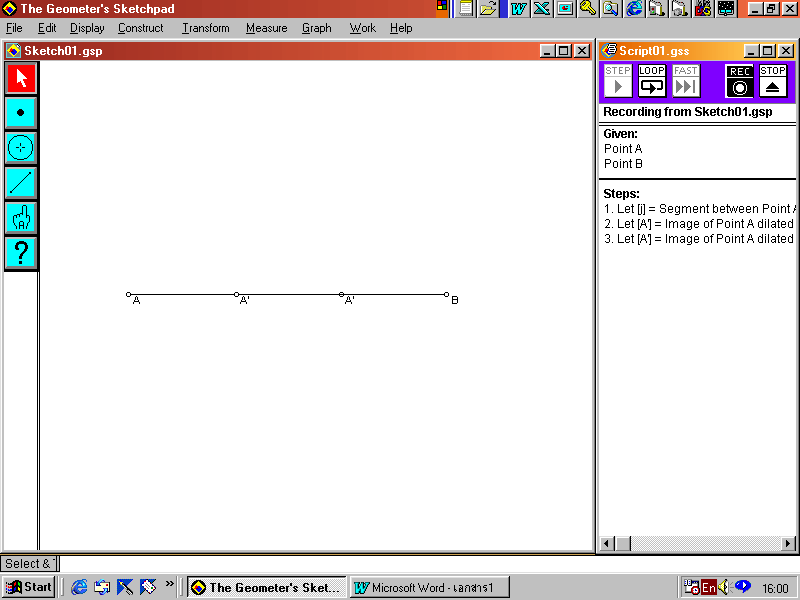
7. จะได้จุด 4 จุดคือ A , A , A , B บนส่วนของเส้นตรง AB ดังรูป
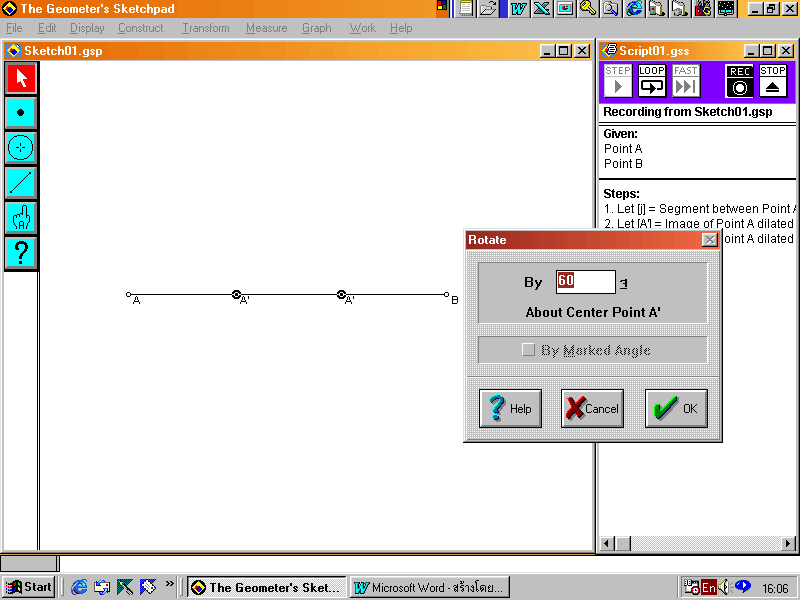
8. เลือกจุด A และจุด A โดยกด Shift ค้างไว้พร้อมกับคลิกที่จุดทั้งสอง ดับเบิลคลิกที่จุดทั้งสอง (ลำดับในการคลิกมีความสำคัญ)
9. คลิกขวา เลือก Transform แล้วเข้าไปที่ Rotate กำหนดค่ามุมเป็น 60 คลิก OK จะได้จุด A
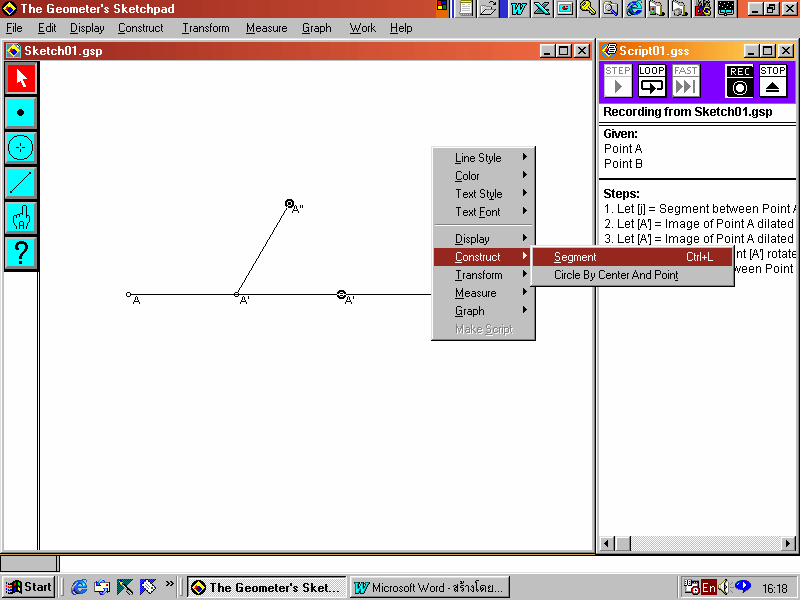
10. ที่จุด A และ จุด A สร้างส่วนของเส้นตรง โดยคลิกขวา แล้วเข้าไปที่ Construct เลือกคำสั่ง Segment จะได้เป็นรูปสามเหลี่ยมด้านเท่า ดังรูป
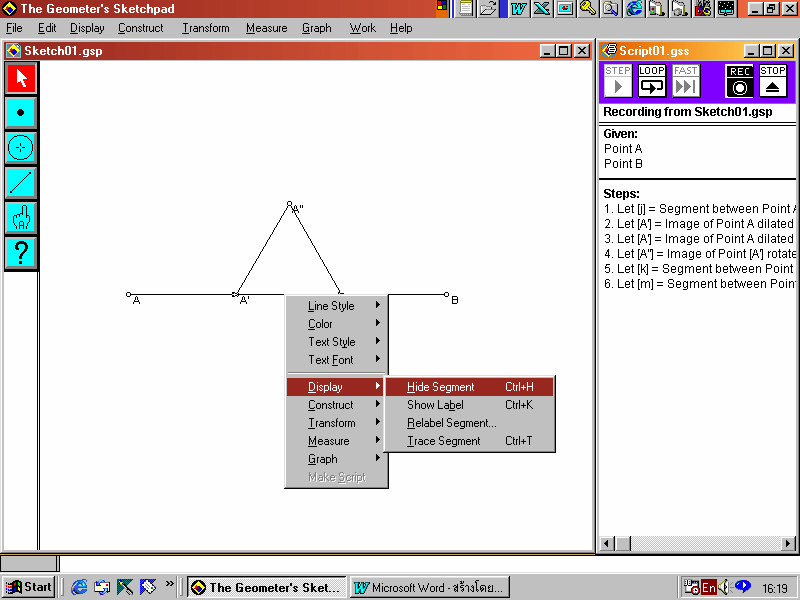
11. คลิกที่ส่วนของเส้นตรง AB คลิกขวา เข้าไปที่ Display แล้วเลือก Hide Segment เพื่อซ่อนส่วนของเส้นตรง AB
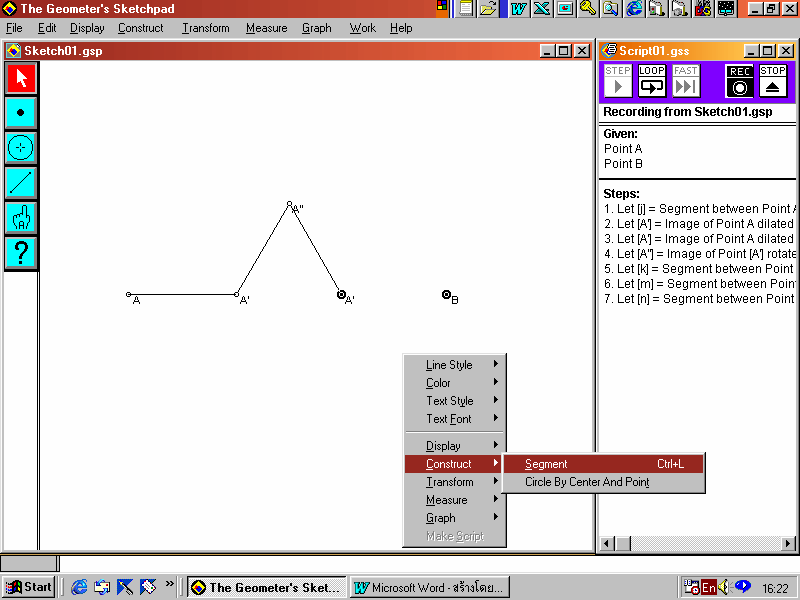
12. สร้างส่วนของเส้นตรงเชื่อมระหว่างจุด A กับจุด A และ จุด B กับจุด Aโดยกด Shift ค้างไว้พร้อมกับคลิกที่จุดทั้งสอง คลิกขวา แล้วเข้าไปที่ Construct แล้วเลือก Segment
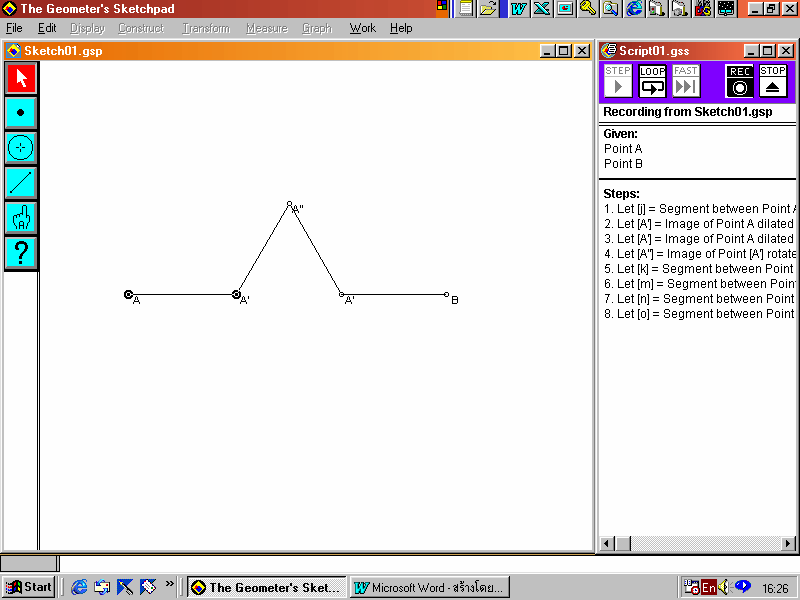
13. เลือกจุด A และจุด A โดยกด Shift ค้างไว้พร้อมกับคลิกที่จุดทั้งสอง ที่หน้าต่าง Script คลิกที่ Loop ทำเช่นเดียวกันกับจุด A และ A , จุด A และ A ,จุด A และ B
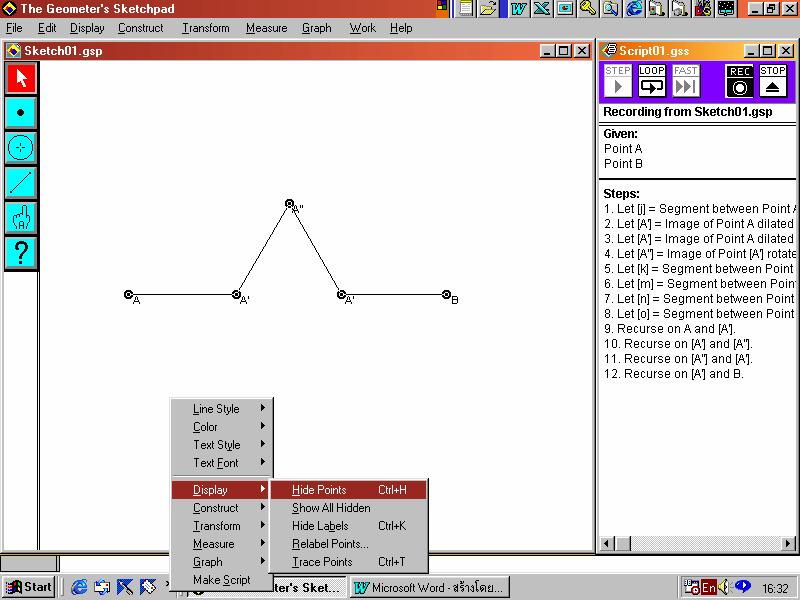
14. เลือกจุดทั้ง 5 โดยกด Shift ค้างไว้พร้อมกับคลิกที่จุดทั้ง 5 คลิกขวาเข้าไปที่ Display แล้วเลือก Hind Points
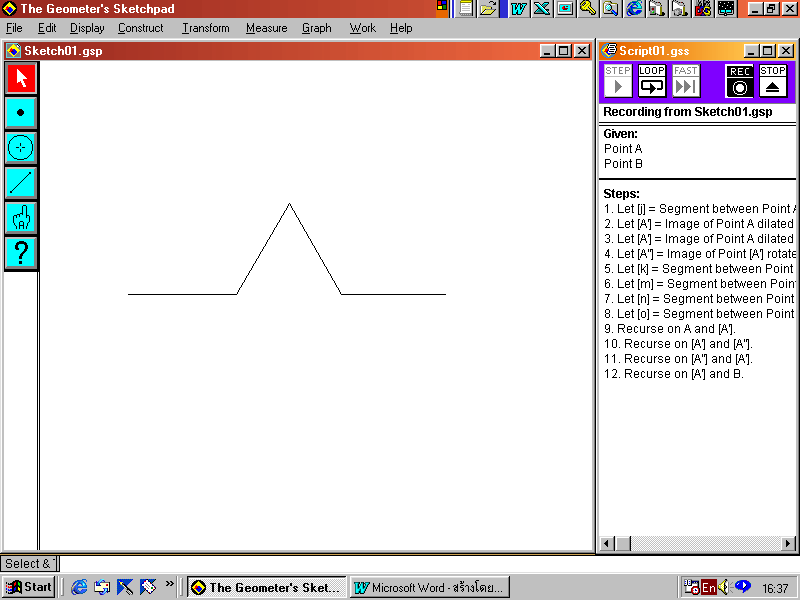
15. คลิก Stop ที่ หน้าต่าง Script
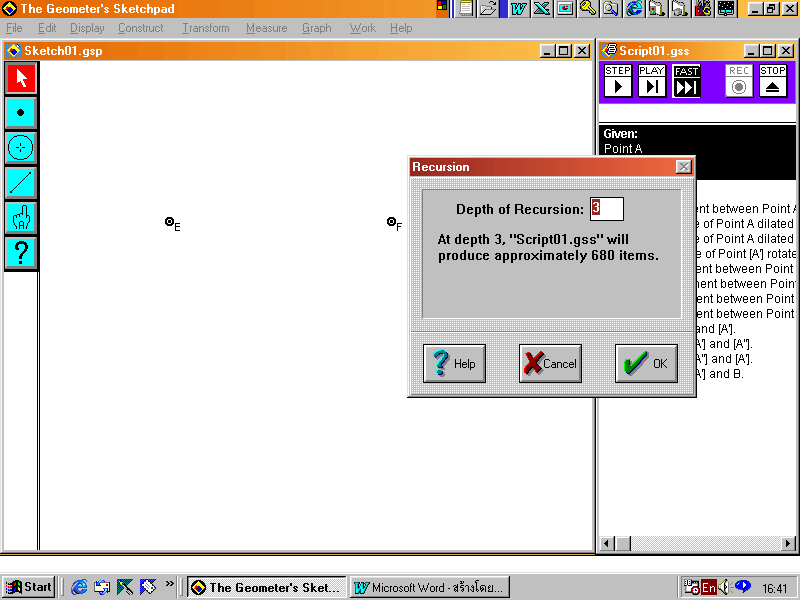
16. คลิกที่ Point tool แล้วสร้างจุดสองจุดที่ Sketch Plane ซึ่งจุดทั้งสองคือ จุด E และจุด F
17. คลิก Fast ที่หน้าต่าง Script กำหนดค่า เป็น 3 คลิก OK
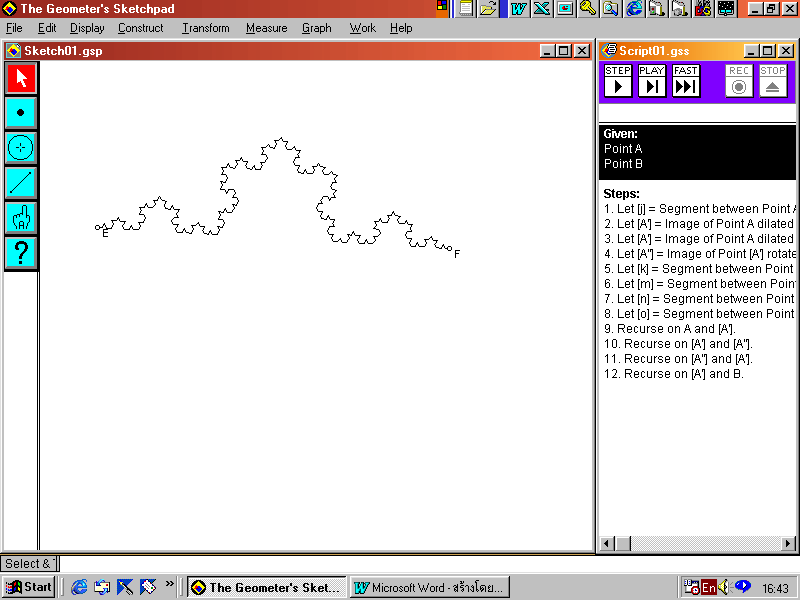
18. จะได้รูป Koch Curve 1 ด้าน แต่เราต้องการสร้างรูป Koch Snowflake ดังนั้นเราต้องนำ Koch Curve 3 ด้านมาประกอบกัน
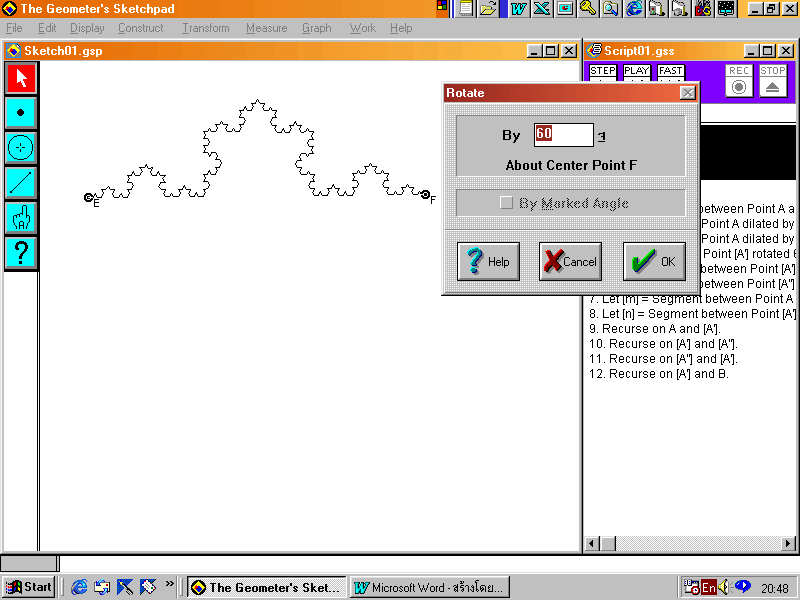
19. เลือกจุด E และจุด F โดยกด Shift ค้างไว้พร้อมกับคลิกที่จุดทั้งสอง ดับเบิลคลิกที่จุดทั้งสอง (ลำดับในการคลิกมีความสำคัญ)
20. คลิกขวา เลือก Transform แล้วเข้าไปที่ Rotate กำหนดค่ามุมเป็น 60 คลิก OK จะได้จุด E
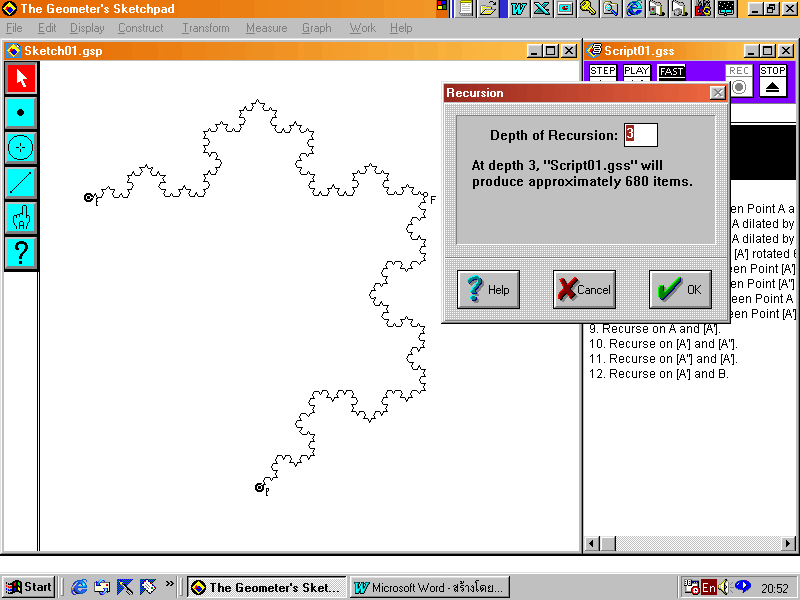
21. สร้างรูป Koch Curve กับทั้ง 3 ด้านของรูปสามเหลี่ยมด้านเท่า ด้วยวิธีเดียวกับข้อ 17.
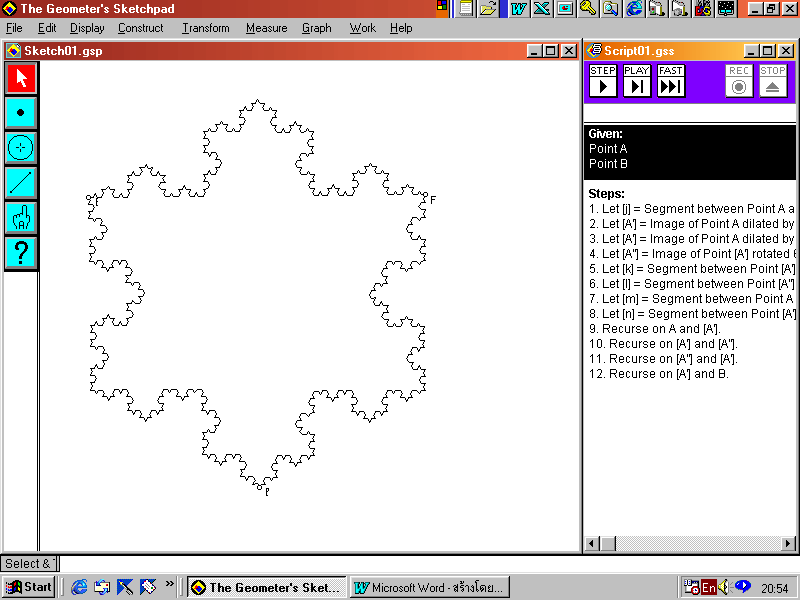
22. Koch Snowflake ที่แต่ละด้านถูกแบ่งด้วยอัตราส่วน 0.33 : 0.33 : 0.33
ในการสร้างรูป Koch Snowflake ให้มีรูปทรงที่เปลี่ยนไปนั้น ทำได้โดย กำหนดค่า Scale Factor ให้แตกต่างกันออกไป ตัวอย่างเช่น
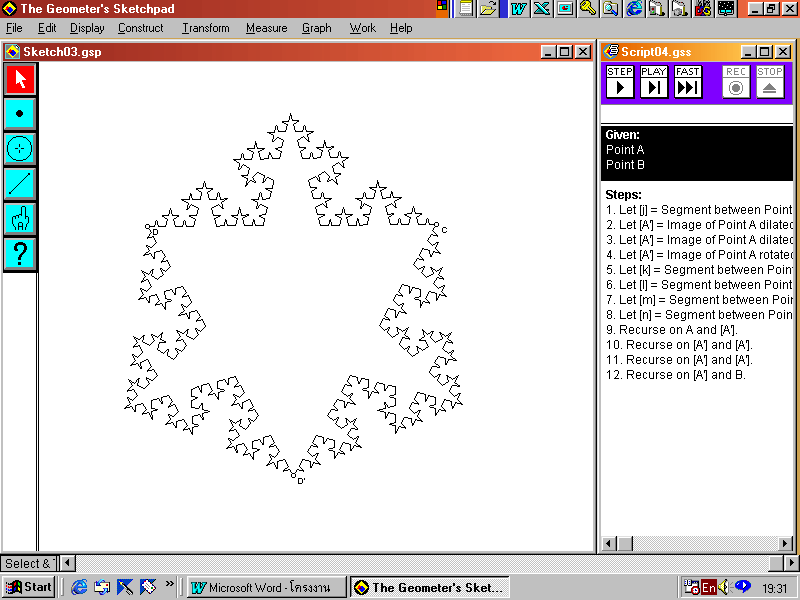
รูปที่ 20 Koch Snowflake ที่กำหนด Scale Factor (New) เป็น 2 และ 6
เมื่อกำหนด Scale Factor (Old) เป็น 10
รูปที่ 21 Koch Snowflake ที่กำหนด Scale Factor (New) เป็น 2.6 และ 7.4 เมื่อกำหนด Scale Factor (Old) เป็น 10
4.4 การหาพื้นที่ของรูป Koch Snowflake ด้วยซอฟต์แวร์ GSP
ในการหาพื้นที่ของรูป Koch Snowflake ด้วย GSP นั้นไม่มีสูตรสำเร็จในการหา เราต้องหาพื้นที่ของรูปสามเหลี่ยมแต่ละขนาดก่อน แล้วนำมาคูณกับจำนวนรูปสามเหลี่ยมที่มีขนาดนั้น จากนั้นจึงนำค่าของพื้นที่ที่ได้ทั้งหมดมาหาผลรวมอีกครั้งหนึ่ง
จำนวนของรูปสามเหลี่ยมที่เราต้องนำไปคูณ จากขนาดใหญ่ไปเล็กตามลำดับ จะมีความสัมพันธ์ ดังนี้
1 , 3 , 12 , 48 , 192 , 768 , 3072 ,
ซึ่งเมื่อจัดให้อยู่ในรูปทั่วไปของลำดับเรขาคณิต จะได้ 1 , 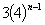
เพราะฉะนั้น จำนวนรูปสามเหลี่ยมทั้งหมดที่เกิดจากการสร้าง Koch Snowflake คือ
 1 ,
1 , 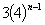
การหาพื้นที่ของรูป Koch Snowflake ด้วย GSP
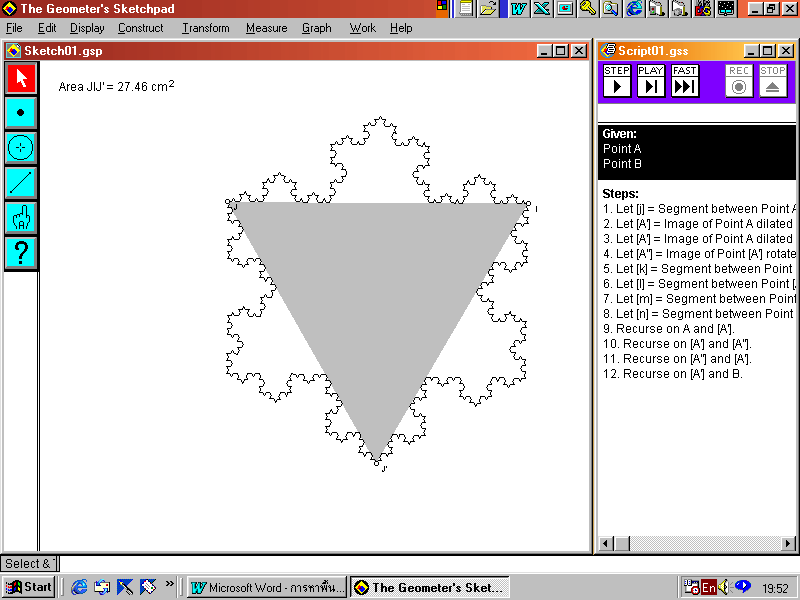
1. หาพื้นที่ของรูปสามเหลี่ยมรูปใหญ่ก่อน โดยกำหนดขอบเขตพื้นที่ที่เราต้องการหา กด Shift ค้างไว้พร้อมกับคลิกที่จุดยอดของรูปสามเหลี่ยม คลิกขวาเข้าไปที่ Construct เลือก Polygon Interior ส่วนที่แรเงา คือส่วนที่เราจะหาพื้นที่
2. คลิกขวาแล้วเข้าไปที่ Measure เลือก Area พื้นที่ของรูปสามเหลี่ยมที่เราต้องการหาจะปรากฏอยู่ด้านบน ซ้ายมือของจอภาพ
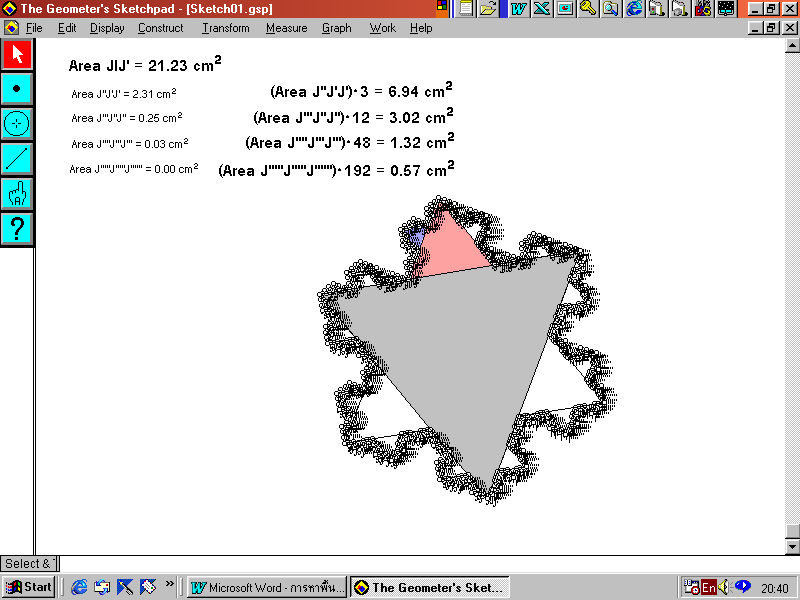
3. ทำเช่นเดียวกับข้อ 1 และ 2 กับรูปสามเหลี่ยมรูปที่มีขนาดเล็กลงตามลำดับ แต่เมื่อได้พื้นที่ของรูปสามเหลี่ยมรูปเล็กแล้ว ต้องนำมาคูณกับจำนวนของรูปสามเหลี่ยมด้วย
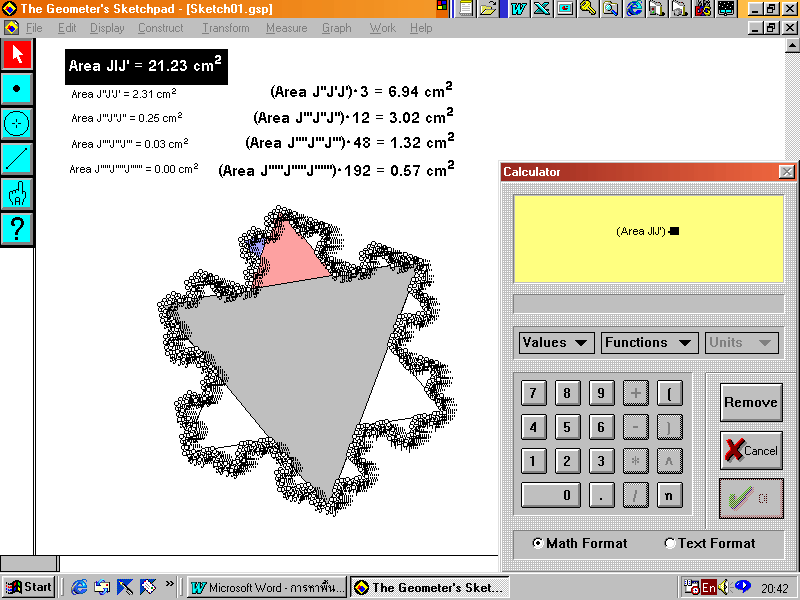
4. เมื่อเราหาพื้นที่ของรูปสามเหลี่ยมทั้งหมดได้แล้วจะแสดงดังภาพ
5. เมื่อเราต้องการหาพื้นที่รวมของรูป Koch Snowflake ทำดังนี้ คลิกขวา แล้วเข้าไปที่ Measure เลือก Calculator จากนั้นดับเบิลคลิกที่ตัวเลขแสดงพื้นที่ที่เราต้องการ หาผลรวมทีละค่า (ในการดับเบิลคลิกค่าต่อไปนั้น เราต้องคลิกที่แป้นเครื่องหมายบวกก่อน) จนครบ คลิก OK
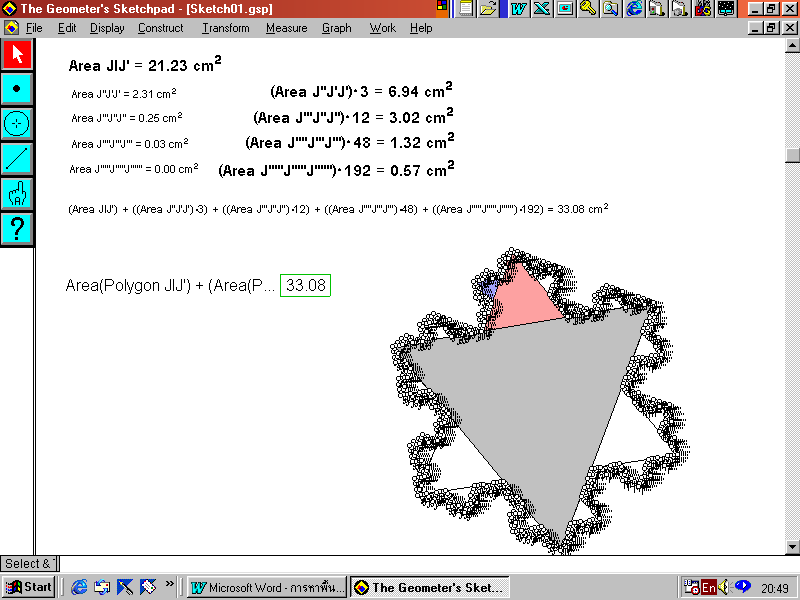
6. ซอฟต์แวร์จะคำนวณพื้นที่ของรูป Koch Snowflake ออกมา และเมื่อเราย่อ หรือขยายรูป ค่าผลรวมที่ได้ก็จะเปลี่ยนไป ซึ่งจะเป็นค่าพื้นที่ของรูปนั้น ๆ ด้วย
4.5 ผลการคำนวณหาพื้นที่ Koch Snowflake โดยใช้สูตรและโดยใช้ GSP
จากการข้างต้นเราสามารถหาพื้นที่ Koch Snowflake ได้ 2 วิธีคือ
- จากสูตร โดย
 เมื่ออัตราส่วน p = q
เมื่ออัตราส่วน p = q
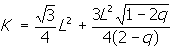 เมื่ออัตราส่วน p ¹ q
เมื่ออัตราส่วน p ¹ q
- การใช้ GSP
ซึ่งผลการคำนวณโดยใช้สูตรและโดยใช้ GSP ได้ผลดังนี้
4.5.1 เมื่ออัตราส่วน p = q
ตารางที่ 1 แสดงค่าของพื้นที่ Koch Snowflake โดยเมื่ออัตราส่วน p = q ที่คำนวณได้จากสูตร และ จาก GSP
|
วิธีการคำนวณ
ความยาว L |
ใช้สูตร
|
ใช้ GSP |
|
3
3.5
4
4.5
5
5.5
6
6.5
7
7.5
8
8.5
9
9.5
10
15
20 |
6.23
8.48
11.08
11.02
17.32
20.95
24.94
29.27
33.94
38.97
44.34
50.65
56.11
62.52
69.28
155.88
277.12 |
6.10
8.33
10.90
13.81
17.07
20.71
24.63
28.92
33.57
38.29
43.60
49.25
55.25
61.60
68.30
153.70
273.37 |
กราฟที่ 1 แสดงความสัมพันธ์ของค่าของพื้นที่ Koch Snowflake โดยเมื่ออัตราส่วน p = q ที่คำนวณได้จากสูตร และจาก GSP
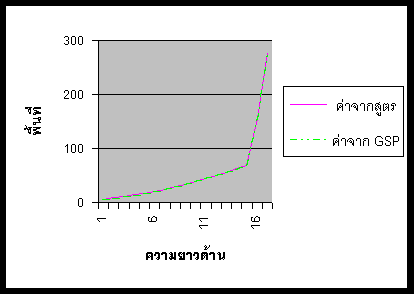
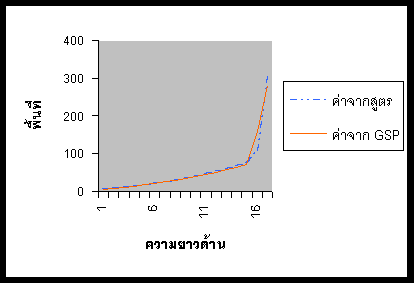
4.5.2 เมื่ออัตราส่วน p ¹q
ตารางที่ 2 แสดงค่าของพื้นที่ Koch Snowflake โดยเมื่ออัตราส่วน p ¹q ที่คำนวณได้จากสูตร และจาก GSP
|
วิธีการคำนวณ
ความยาว L |
ใช้สูตร
|
ใช้ GSP |
|
3
3.5
4
4.5
5
5.5
6
6.5
7
7.5
8
8.5
9
9.5
10
15
20 |
6.80
9.25
12.09
15.30
18.89
22.85
27.20
31.93
37.03
42.51
48.36
54.60
61.21
68.20
75.57
107.04
302.30 |
6.33
8.62
11.23
14.22
17.55
21.25
25.31
29.72
34.23
39.34
44.87
50.66
56.82
63.33
70.18
157.97
280.74 |
กราฟที่ 2 แสดงความสัมพันธ์ของค่าของพื้นที่ Koch Snowflake โดยเมื่ออัตราส่วน p ¹q ที่คำนวณได้จากสูตร และจาก GSP