|
Atardecer
desde el espacio. Nasa. JPL |
Guía
Astronómica Gonzalo
Duque-Escobar, P. As.
Universidad
Nacional de Colombia Manizales, 1992 |
GUIA
Nº 2
La
esfera celeste es una esfera de
radio infinito, o unitario si se quiere, en cuyo centro se encuentra el observador.
Allí la Tierra se reduce a un punto.
Si
prolongamos infinitamente el eje de rotación de la Tierra, con sus extremos interceptamos
la esfera celeste en los polos P y P'. Si prolongamos infinitamente nuestro horizonte
generaremos un círculo máximo denotado con los cuatro puntos cardinales en los extremos
de dos diámetros suyos.
El
horizonte divide la esfera celeste en dos hemisferios: el hemisferio visible, que contiene
el cenit y el invisible que queda por debajo del observador. Los astros aparecen sobre el
horizonte por el costado E y se ocultan por el costado W. Dependiendo de la latitud,
algunos astros nunca se ocultan y otros nunca aparecen sobre el horizonte.
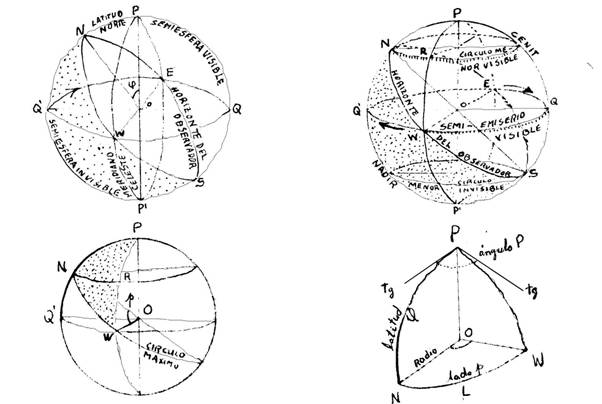
Figura
2. El triángulo esférico y el horizonte del observador.
Considere
el astro R. El observador está en el centro
de la esfera celeste, que se considera de radio infinito. El astro tiene por trayectoria
un círculo menor de declinación, perpendicular al eje polar PP'.
Los
triángulos esféricos como NPW y PEQ
deben estar limitados por tres arcos de círculos máximos. NPR no será triángulo
esférico, a cuenta del arco NR que no pertenece a ningún círculo máximo.
Los
astros giran de E a Q y de Q a W, siendo visibles sobre el horizonte. Sus trayectorias son
círculos menores perpendiculares a PP'. (Z es el cenit).
1.
ELEMENTOS DE POSICION
Las
coordenadas son un valor, por ejemplo la distancia o el ángulo en una dirección dada
(hacia arriba, hacia abajo, a la izquierda, a la derecha), que se utiliza con uno u otros
más para describir la posición de un objeto.
Círculo
máximo es cualquier
círculo de la esfera celeste que tiene a la Tierra por centro como el ecuador celeste, la
eclíptica y todas las líneas de ascensión recta. Los círculos menores son los que no
tienen a la Tierra por centro. Las líneas de declinación (círculos perpendiculares al
eje polar) distintas del ecuador celeste son círculos menores.
El cenit
es el punto de la esfera celeste que se encuentra directamente por encima de la cabeza de
un observador.
El nadir
es el punto de la esfera celeste que se encuentra directamente
por debajo de un observador. El nadir está situado a 180° del cennit, pues uno
y otro son puntos antípodas.
Los polos
celestes están situados sobre la esfera celeste, directamente encima de los polos de
la Tierra. Están contenidos por el eje polar de la esfera celeste, que es la
prolongación infinita del eje de los polos geográficos del planeta.
El
ecuador celeste es el ccírculo
máximo identificado con Q. Dicho círculo contiene el este y el oeste (E y W). También
el ecuador celeste es la intersección que resulta sobre la esfera cuando el plano del
Ecuador de la Tierra se prolonga al infinito.
Eclíptica
es el recorrido que parece seguir el Sol alrededor de la esfera celeste cada año. Ya que
la Tierra describe una órbita alrededor del Sol, éste parece moverse a lo largo de la
eclíptica. Esta última es un círculo máximo inclinado 23½ grados con respecto al
ecuador celeste. Su nombre se debe a que sobre tal círculo se producen los eclipses
de Sol.
Horizonte
es un plano infinito perpendicular al radio de la Tierra, que se extiende adelante y
atrás del observador, y a derecha e izquierda suya. Todos sus puntos ubicados sobre la
esfera celeste están a 90° del cenit y el nadir.
El horizonte contiene los puntos cardinales así: de pie el observador y con la mano
derecha por donde nace el Sol, tendrá enfrente el norte y a su espalda el sur, a la
derecha el oriente y por la izquierda el occidente.
El acimut
A, es la dirección de un objeto, medida en grados alrededor del horizonte del
observador, en el sentido de las agujas del reloj desde el sur. Es, entonces, el acimut un
ángulo horizontal que varía de 0° a 360°. Aquí se ha definido
un acimut sur directo, pero en topografía el acimut suele ser norte, y eventualmente se
puede considerar acimut retrógrado.
La ascensión
recta es una medida angular sobre el ecuador celeste; por asociación, es lo mismo que
la longitud sobre la Tierra; por equivalencia, se mide en horas, minutos y segundos (de
tiempo), hacia el Este, a lo largo del ecuador celeste y partiendo de cero en el
equinoccio de primavera (t). Su símbolo es a.
La declinación
se mide sobre un círculo de la esfera celeste, que contenga el eje de los polos; dicho
círculo es el meridiano celeste del astro, igual que la latitud sobre la Tierra y
se mide en grados norte (+) o sur (-) a partir del ecuador celeste; su símbolo es d.
2.
COORDENADAS ASTRONOMICAS
2.1
Coordenadas Ecuatoriales: los círculos
fundamentales son el ecuador celeste y el primer meridiano celeste. El ecuador celeste se
denomina QQ' y el primer meridiano, que le es perpendicular, pasa por Q. Para la
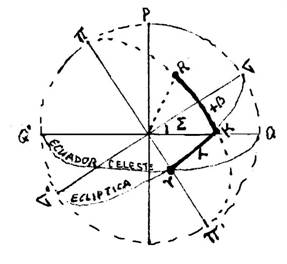
ascensión recta el origen es la intersección del ecuador celeste con la eclíptica (no dibujada), en el punto Aries
o punto t, que se denomina también punto vernal o equinoccio de primavera. La
distancia S entre Q y t (llamada tiempo sidéreo del punto vernal), es una de las
relaciones fundamentales para el cálculo. Se mide en sentido retrógrado desde el
meridiano de Greenwich, que contiene el punto Q.
|
tK = a ascensión
recta en horas y en sentido retrógrado, medida desde el punto t. QK = t ángulo
horario en horas y en sentido directo, medido desde el meridiano superior. KR = ± d declinación
en grados, siendo positiva en dirección a P y negativa hacia P'. P y P'=
polos celestes sobre el eje del mundo. t es el
punto vernal o punto Aries a + t = S tiempo sidéreo del punto vernal |
Figura
3. Astro R, determinado por la ascensión recta y la declinación.
2.2
Coordenadas Horizontales: aquí los círculos
fundamentales son el horizonte del observador y el primer vertical. Perpendicular al
círculo del horizonte, se tiene la línea cenit-nadir. El horizonte es el círculo NS,
que contiene los cuatro puntos cardinales. El primer vertical contiene el sur, porque los
acimutes son sur-directos. La distancia PN es la latitud del observador, f. Un
círculo vertical es cualquier círculo máximo que contenga el cenit y el nadir.
|
SK = Az
acimut sur retrógrado en grados, medido
sobre el horizonte astronómico del
observador. KR = ±
h altura sobre el horizonte, ZR = ?
distancia cenital, medida en grados. Este
ángulo es complemento de h. Z y Z'
= cenit y nadir del observador sobre la vertical. PN =
f latitud del observador |
Figura
4. Astro R, determinado por el acimut sur directo y la distancia cenital.
2.3
Coordenadas Eclípticas: los círculos
fundamentales son el plano de la eclíptica y el círculo máximo perpendicular a la
eclíptica, que contiene el punto Aries o punto vernal t. El ángulo S que hacen el
ecuador celeste QQ' y la eclíptica ss', se debe a la inclinación del eje de la Tierra,
que no resulta perpendicular a la órbita. Esta es la causa de las estaciones.
Sobre
la eclíptica hay cuatro puntos fundamentales: los equinoccios de primavera (t) y otoño
(O) y los solsticios de invierno (dic. 21) y verano (jun. 21). Hay dos meridianos celestes
llamados coluros: el de los solsticios que pasa por los polos eclípticos, y el de los
equinoccios.
|
tK = ? longitud astronómica medida en grados y en
sentido retrógrado. KR = ±
ß latitud astronómica medida en grados t es el
punto vernal, intersección del ecuador celeste QQ' y la eclíptica ss' igual a
la inclinación del eje terrestre, y por lo tanto igual al arco Pp |
Figura
5. Astro R, determinado por la latitud y la longitud eclípticas.
2.4
Coordenadas galácticas: la latitud
galáctica b es la distancia angular de una estrella a partir de un círculo máximo
definido como una línea media de la Vía Láctea o ecuador galáctico; los valores
positivos indican posiciones al norte del ecuador galáctico, los negativos posiciones al
sur del mismo. Lógicamente hay dos polos galácticos, uno norte y otro sur.
Se
tomó como punto cero de la longitud galáctica un punto de la constelación de Sagitario,
el que se supone con gran seguridad coincide con la dirección del centro de nuestra
Galaxia.
3.
TRIANGULO POLO CENIT ASTRO
Si
queremos permutar los dos primeros sistemas de coordenadas, ecuatoriales y horizontales
debemos resolver el triángulo Polo Cenit Astro. Siendo R el astro, tenemos:
Para
transformar coordenadas, la expresión:
R(a, d)
= R (t, d) ®¬ R(Az, h) = R (Az,?)
alude a
los dos sistemas de coordenadas intercambiables, pues generalmente las coordenadas, que
vienen en las efemérides y catálogos de estrellas, aparecen en el sistema ecuatorial,
dado que son valores universales. Cada observador en particular, desde su propio lugar en
el planeta, pretenderá conocer el acimut y altura sobre el horizonte de un astro
cualquiera del catálogo, o en su defecto, querrá él identificar un astro que tiene en el cielo, buscándolo
posteriormente en el catálogo de estrellas.
3.1
Las tres relaciones básicas, para el cálculo
f = ? +
d => llatitud del
observador; que alude a la distancia angular PN, entre el polo celeste y el norte
geográfico.
S = t +
a => ttiempo
sidéreo del punto vernal, como se señaló en el sistema de coordenadas ecuatoriales.
S = 23° 27'
=> ángulo entre QQ' y ss', debido a la inclinación del eje de la Tierra. Es también
el ángulo entre PP' y pp', que son los ejes del mundo y de los polos eclípticos
respectivamente.
NOTA:
La ascensión recta se mide en sentido retrógrado con respecto al P. El ángulo horario
en sentido directo. El acimut astronómico se mide en sentido directo con relación al
cenit.
A
continuación mostraremos el triángulo polo-cenit-astro, considerando tanto un astro del
occidente, como uno del oriente. De ésta manera las fórmulas trigonométricas no
presentarán problemas de signo en algunas de las funciones.
ASTRO DEL W
ASTRO DEL E
|
3.2.
Las tres leyes para el cálculo de los triángulos esféricos
De la
trigonometría esférica se pueden obtener tres relaciones fundamentales. Recordamos que
un triángulo esférico se conforma por tres arcos de círculos máximo, razón por la
cual sus lados pueden medirse en unidades de arco. Llamamos los lados con minúsculas a,
b, y c y sus ángulos con las mayúsculas A, B y C correspondientes, según la notación
clásica.
|
Figura
7. Notación convencional para un triángulo esférico ABC, y su equivalencia en el
triángulo Polo-Cenit-Astro: PZR.
Partiendo
de las relaciones:
1. cos
a = cos b cos c + sen b sen c cos A
2. sen a
cos B = cos b sen c - sen b cos c cos A
3. sen a
sen B = sen b sen A
Aplicación
en el triángulo Polo Cenit Astro (PZR): (sólo esta figura).
Para el
efecto, como a modo de diccionario, sustituimos en las fórmulas anteriores los valores
que se dan de los lados y ángulos, entendiendo que los valores homólogos, al comparar el
triángulo ABC con el triángulo PZR, son en su orden:
Lados |
Angulos |
Unidad de tiempo Vs Unidad de Arco
|
a
= ? |
A = t |
1
hora «
15°
sex |
b
= 90°
- d |
B
= 180°
- Az |
1
min «
15' sex |
c
= 90°
- f |
C
= R |
1
seg «
15" sex |
|
Figura
8. Los seis elementos del triángulo PZR, para permutar coordenadas ecuatoriales y
horizontales entre sí.
Las
seis relaciones de lados y ángulos nos permiten hacer una sustitución directa, para
transformar las anteriores expresiones en las que se muestran a continuación, que ya
incluyen algunas simplificaciones trigonométricas al hacer las co- funciones de los
ángulos complementarios y suplementarios.
cos ? =
sen d sen f + cos d cos f cos t
(1)
sen ? cos Az = -sen d cos f + cos d sen f cos t (2)
sen ? sen Az = cos d sen t
(3)
El
ángulo en R no interesa en la solución. Supongamos que deseamos las coordenadas
horizontales de un astro cuyas coordenadas ecuatoriales se obtuvieron a partir de un
catálogo o una efemérides o resolver el caso contrario, para conocer un astro observado
pero que aún no ha sido identificado.
Con d y
t calculo ?
en
(1)
(para el efecto, f depende del observador)
Con ?
calculo Az en
(2)
( ? se ha obtenido y d y t son conocidos)