|
Panorámica de la Nebulosa de Orión.
Sel.noaa.gov |
Guía Astronómica Gonzalo Duque-Escobar, P. As.
Universidad Nacional de Colombia Manizales, 1992 |
GUIA Nº 11
EL UNIVERSO
1.
INSTRUMENTOS PARA OBSERVAR ASTROS
Supuesta
la inmensa distancia que nos separa de los cuerpos celeste, el ojo humano
es un instrumento insuficiente para proporcionarnos una visión detallada del Universo.
Por ello resulta prodigioso que el hombre, antes de la invención del
telescopio, llegara a medir con gran exactitud los movimientos de los astros,
calcular los eclipses, intuir la estructura del sistema solar y a determinar
las leyes que rigen sus órbitas.
1.1
Telescopios
Pero
fue a partir de la invención del telescopio, a comienzos del siglo XVII, cuando
el observador del cielo encontró el instrumento capaz de acercarle los astros,
y cuando la ciencia del cielo progresó con rapidez.
|
|
Figura
50. Principales telescopios: arriba, Telescopio de Galileo o refractor
(objetivo de lente); centro, Telescopio
de Newton o reflector (espejo parabólico); abajo, cámara de de
Schmidt, espejo de gran campo de visión, gracias a la placa de corrección
y a la lente de curvatura esférica.
Un
telescopio astronómico puede ser, fundamentalmente, de dos tipos: de lente (refractor)
o de espejo (reflector). El primero está formado por una gran lente
(objetivo), que recibe la luz de cualquier objeto luminoso y concentra su
imagen en un punto (el foco), situado a determinada distancia F -la existente
entre el centro óptico de la lente y el punto en el cual se forma la imagen de
un objeto muy alejado-; una segunda lente, mucho menor, amplía los detalles de
la imagen formada por el objetivo. En el reflector, el objetivo no es
una lente, sino un espejo cóncavo, que concentra la imagen también en un punto focal; el ocular es siempre
una lente que amplía esta imagen. Cabe destacar que cuanto mayor es el objetivo
(lente o espejo), más luminosa y mejor definida es la imagen; cuanto más larga
es la distancia focal F, mayor es el aumento, pero menor la luminosidad. Lo
mismo ocurre con los oculares: un ocular amplio, da una imagen muy luminosa
pero poco aumentada; un ocular de foco corto proporciona grandes aumentos, pero
la imagen es más oscura y menos nítida.
Si
la distancia focal del objetivo es F y la del ocular f, y si el diámetro del
objetivo es φ, de dos parámetros depende la capacidad de un
telescopio: de los aumentos y de la razón focal.
Los
aumentos son A = F/f
La
razón focal es R = F/φ
Si
un telescopio de lente presenta valores de F=900 mm y φ = 60 mm, y
posee dos oculares, uno de f=22,5mm y otro de 45 mm,
Con
el primero se observarán imágenes más grandes y con el segundo imágenes más
luminosas. Además el máximo aumento para observación terrestre, es el resultado
de multiplicar por 13 el número de centímetros del diámetro del objetivo, o por
26 si es para observar imágenes luminosas y bien contrastadas. Para el caso
anterior, el máximo valor de los aumentos es A =13x6= 78X ( que se lee 78
veces) o el doble de aumentos, si es para imágenes bien contrastadas.
Montajes
de telescopios: la funnción del montaje del telescopio es
doble. Primero, debe mantener firmemente fijo el telescopio en todas las
condiciones, para que la imagen grandemente ampliada pueda contemplarse y
fotografiarse. En segundo lugar, tiene que haber un medio sencillo de mover el
telescopio, de modo que éste pueda seguir a la estrella en su movimiento
aparente a través del firmamento, debido a la rotación de la Tierra.
Montaje
altacimut: es el más simple, para medir la altura de los cuerpos
celestes. El telescopio va montado sobre dos ejes, uno vertical y otro
horizontal. Alrededor del segundo, el telescopio da vueltas de campana. La
rotación del telescopio alrededor de su eje vertical, se realizará
barriendo el acimut en el horizonte, para permitir levantar y bajar el
telescopio de altura, entre el cenit y el nadir. Sistema similar al del
teodolito.
Montaje
ecuatorial: si movemos el eje
vertical hasta que sea paralelo al eje de la Tierra y lo fijamos en ese
ángulo, bastará la rotación del telescopio alrededor de este eje (el eje
polar), para permitir al observador seguir esa estrella. Hecho este
basculamiento, el que antes era el círculo horizontal, se transformará en un
círculo paralelo al ecuador de la Tierra. Generalmente, el montaje lleva
acoplado un motor para hacer girar el telescopio alrededor del eje polar
a la velocidad exacta de la rotación de la Tierra, para eliminar el movimiento
aparente de las estrellas. Se puede disponer también de relojes solares y
lunares, a fin de sostener ambos astros en la visual.
Radiotelescopios:
antenas que actúan como espejos parabólicos, cuya curvatura es de la forma Y =
x2/F. La superficie reflectante reúne las ondas de radio en el foco,
igual que un espejo óptico. Un dipolo o una antena de bocina, recoge allí la
radiación y la envía al amplificador del telescopio. Estos aparatos,
destinados a captar radiaciones de grandes longitudes de onda a menudo se
construyen de malla de alambre.
Radiointerferómetro:
instrumento que mejora el poder de resolución de las radioantenas. Consiste en
dos (o más) radiotelescopios, situados a la mayor distancia posible entre sí.
Ambos instrumentos van conectados a un receptor. Al pasar una radiofuente por
el meridiano, las ondas reflejadas por ambos espejos crean, por interferencia,
una serie de reforzamientos y extinciones en el receptor, que permiten
localizar una radiofuente, con una exactitud que supera la de un sólo espejo.
|
|
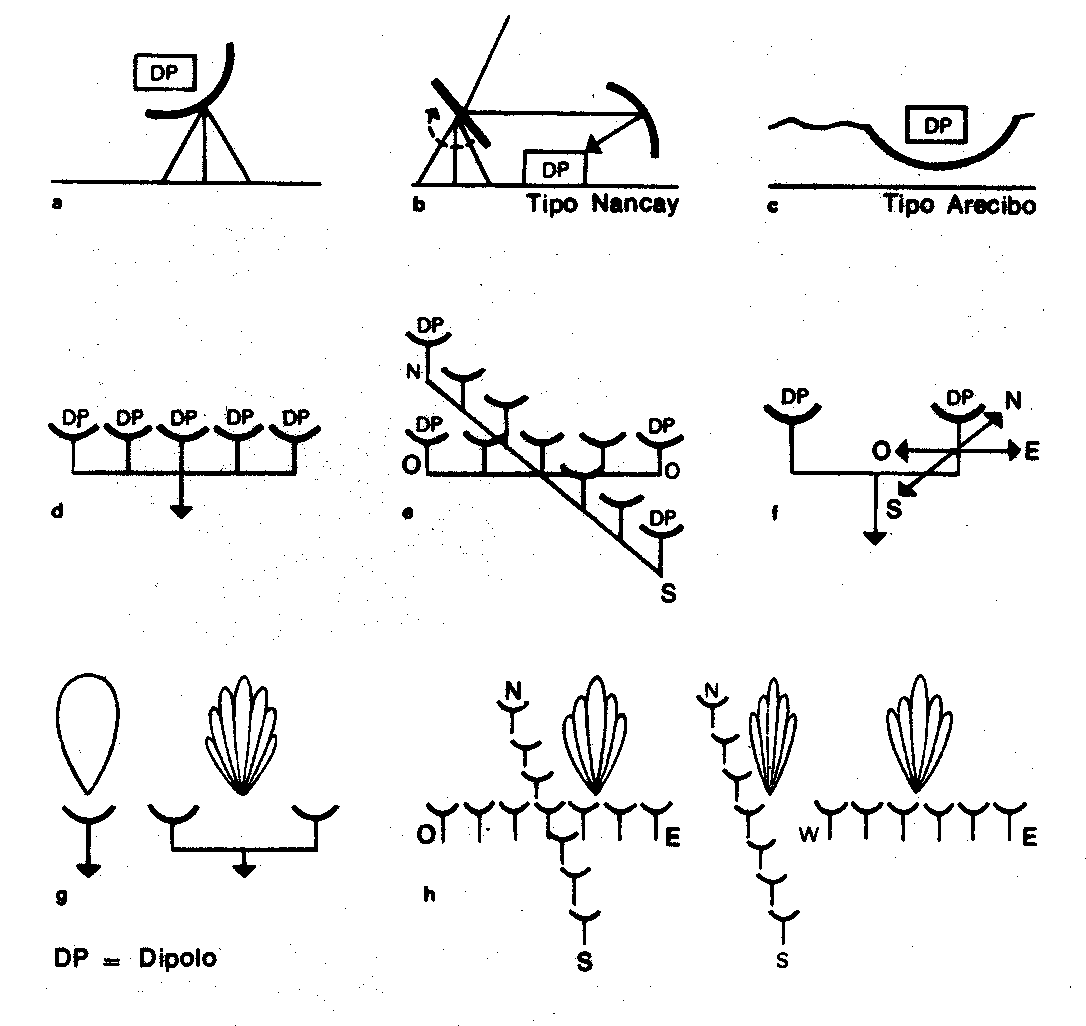
a, de espejo parabólico, diámetro hasta 100m, buena sensibilidad
pero demanda buena superficie para separar. b y
c,instrumentos de paso con 1 o 2 antenas reflectantes, diámetro en Arecibo
305m. Una bandeja esférica o dos antenas reflectantes d,
redes de difracción lineales, la base puede extenderse entre continentes.
Gran poder de separación. e,
Rejilla de alambres en cruz. c/u 1600m. Gran poder de separación y poca
sensibilidad. f, Apertura
Synthesis, dos pequeñas antenas conectadas que se desplazan sobre un riel.
gran poder de separación y tiempo largo de observación. g y
h, interferómetros con antena individual (baja separación) y con doble antena
(alta separación). |
Figura
51. Radiotelescopios de pantalla parabólica con antena(dipolo) en el foco, o
como sistemas de antenas, que puede conformar un interferómetro para aumentar
su poder de separación. Fuente: Diccionario Rioduero. Física del Espacio.
1.2
Espectros
El
espectro electromagnético: la energía radiante se
propaga por ondas electromagnéticas a la velocidad de la luz (c = 300.000
kilómetros por segundo).
|
|
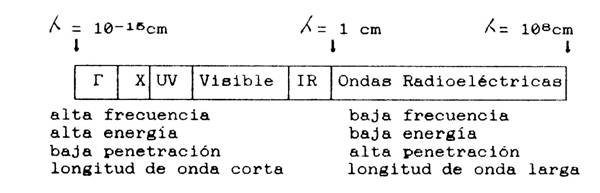
Figura
52. Espectro electromagnético, desde la radiación gamma hasta las ondas de
radar. Incluye rayos gamma, rayos X, radiación ultravioleta, toda la luz entre
el azul y el rojo, el infrarrojo, y las ondas cortas y largas.
El
espectro visible: cuandoo la luz atraviesa un medio de
densidad variable o pasa de un medio a otro de diferente densidad (por ejemplo,
del aire caliente al frío, o del aire al agua, o del agua a un cristal), se
altera la velocidad del rayo de luz y el rayo se dobla o se refracta. Bajo
ciertas condiciones esto resulta en un desdoblamiento del rayo de luz
blanca en bandas de colores -rojo, naranja, amarillo, verde, azul, morado y
violeta-.
|
|
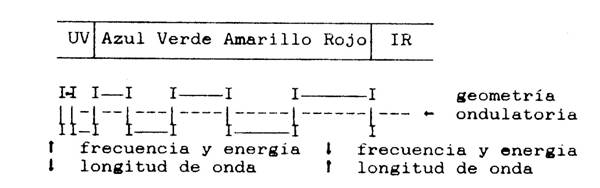
Figura
53. La luz blanca se descompone en un conjunto de colores llamados primarios
(azul, amarillo y rojo); cada uno de ellos con una frecuencia específica. El
verde es la combinación de los dos primeros y el naranja de los dos últimos.
El
arco iris es el resultado de unos de estos acontecimientos:
un observador, de pie y de espaldas al Sol, que contemple una lluvia, ve el
arco formado por la luz que atraviesa las gotas individuales de lluvia, donde
se refracta, se disocia y se refleja hacia su ojo. El arco común o primario,
rojo en la cara externa y violeta en la interna, se forma en las gotas de
lluvia situadas en ángulo de aproximadamente 24°
respecto a una línea imaginaria, que va del Sol a un punto del suelo delante
del observador y que atraviesa el ojo de éste -un punto que es también el
centro del arco-. Si el Sol está muy cerca del horizonte, el arco formará un
semicírculo y cuanto más alto está el Sol en el cielo, tanto más plano será el
arco, de tal manera que superando el Sol los 42°
sobre el horizonte, no se verá arco iris alguno.
1.3
Líneas espectrales
Con
el análisis del espectro de la energía radiante se puede conocer la
temperatura, composición y velocidad radial de los objetos celestes. El calor
informa de la temperatura. Los rayos espectrales oscuros o brillantes de los
elementos y el desplazamiento del espectro, hacia el IR o el UV, de la
velocidad según el efecto Doppler.
Espectro
continuo: producido por cuerpos incandescentes sólidos o
líquidos, así como por los gases a muy alta presión y gran temperatura, dan un
espectro continuo sin rayas.
Espectro
de emisión: los gases luminiscentes, a presiones o
temperaturas más bajas, muestran rayas de emisión claras e individualizadas.
Cada elemento químico emite su propia serie de rayas. El espectro luminoso de
cualquier gas, revela su composición química.
Espectro
de absorción: si la luz de cualquier cuerpo -que de suyo
daría un espectro continuo- atraviesa un gas a menor temperatura, aparece sobre
el continuo una serie de rayas oscuras (rayas de absorción o de Fraunhofer),
precisamente en aquellas longitudes de onda para las que el gas, radiante él
sólo, habría generado rayas de emisión. Esto vale para la mayoría de las
estrellas y para el Sol, donde los rayos luminosos que provienen de zonas más
profundas atraviesan capas externas frías y generan allí las rayas de
Fraunhofer.
|
|
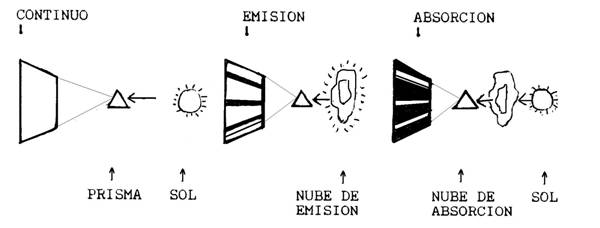
Figura
54. Tres tipos de espectros, según la fuente luminosa.
En
el interior de las estrellas, donde reinan presiones y temperaturas muy altas,
abundan los electrones libres. Como las órbitas a las que saltan los electrones
son muy diversas, el espectro es en principio continuo. Aparte del hidrógeno
están también otros elementos más pesados y complejos, pero el principio es el
mismo. En las capas más externas y frías de la estrella los átomos de
hidrógeno, por ejemplo, toman aquellas cantidades de energía que necesitan para
excitar sus electrones (para elevarlos por ejemplo, de la órbita 2 a la 3). De
esta manera se forma una raya de absorción.
Según
la Ley de Planck los objetos fríos emiten más el IR (infrarrojo) y los objetos
calientes emiten más el UV (ultravioleta). Tan importante es la ecuación E =
hf, donde h es la constante de Planck y f la frecuencia, como la ecuación
de Einstein que alude a la misma magnitud: E = mc2.
Se
entiende por radiación de un cuerpo negro la radiación electromagnética emitida
por un cuerpo negro ideal. Es la cantidad máxima teórica de energía radiante de
todas las longitudes de onda, emitida por un cuerpo negro a una
temperatura determinada.
2.
EFECTO DOPPLER
Supongamos
un satélite enviando una señal luminosa. El efecto para un receptor inmóvil es
similar al que se estudia en la acústica, que escucha el sonido, con una alta
frecuencia cuando la fuente se acerca y
con una baja frecuencia cuando ella se aleja.
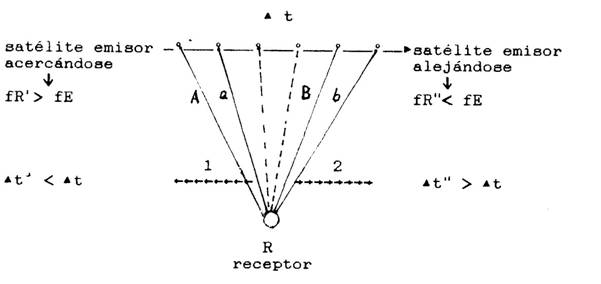
Volviendo
a la fuente luminosa en movimiento, si la frecuencia de emisión fE es constante
(Ù
t no varía), la frecuencia de recepción si varía: en 1 es más alta y en 2 es
más baja. Las frecuencias recibidas fR se modifican así: las distancias recorridas por el haz
luminoso, A y a son crecientes cuando la fuente se acerca por la
izquierda al observador, con lo cual fR' mayor que fE (en aproximación).
Después de pasar el satélite, sobre el observador, empezará a irse, de tal
manera, que las distancias a la fuente como B y b se harán cada vez más largas;
con ello la fR" será menor que la fE (en alejamiento). Sobra subrayar que
la velocidad de la señal es constante al recorrer cualquier distancia entre la
fuente y el receptor; en el caso c.
|
|
Figura
55. Satélite en movimiento que envía una señal a un receptor fijo R. Con Ù
t se señala el intervalo de tiempo entre señales consecutivas. El inverso de Ù
t es la frecuencia.
2.1
Cálculo de la velocidad de una estrella
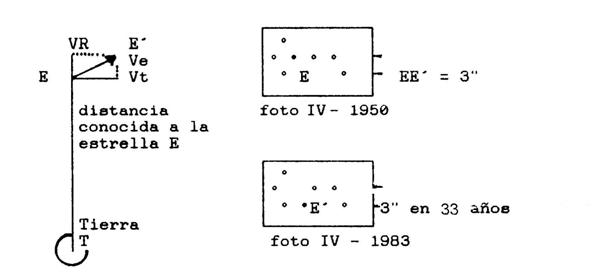
Velocidad
espacial de una estrella E vista desde la Tierra T: el vector de velocidad
espacial, Ve, tiene dos componentes con relación a la visual del observador.
Una en su dirección, VR, y otra normal a ella, Vt. Se puede conocer la magnitud
de la velocidad espacial o total Ve, si medimos las velocidades tangencial Vt y
radial VR. Aplicando Pitágoras:
Ve
= ( Vt 2 + VR 2 )1/2
VR
se puede conocer por el desplazamiento del espectro al infrarrojo (rojo) o al
violeta (azul), según el efecto Doppler.
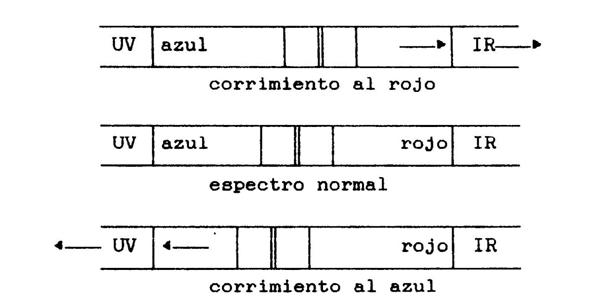
Si
un astro se aleja el espectro se corre al rojo, la magnitud del corrimiento
depende de la magnitud de la velocidad radial VR. Si un astro se acerca el
espectro se corre al azul, a mayor velocidad radial VR, mayor corrimiento de
las líneas espectrales.
|
|
Figura
56. Las líneas espectrales ponen en evidencia la velocidad radial de un astro.
El espectro del centro no muestra corrimiento.
|
|
Figura
57. Cambio en la posición de una estrella cercana, con relación a las estrellas
de fondo, al cabo de 33 años
La
velocidad tangencial, Vt se conoce comparando fotografías de
épocas diferentes que muestran el corrimiento angular de la estrella E,
respecto a las estrellas lejanas. Para este cálculo se debe conocerse la
distancia de la Tierra a la estrella TE, que se obtiene por el método de la
paralaje.
3.
ESTRUCTURA DEL UNIVERSO OBSERVABLE
Halley
(1656-1742), concebía un Universo eterno e infinito; como prueba de ello
se tenía, que al observar los astros "firmes" en el cielo, no era
posible señalar punto alguno sobre el cual estuviese colapsando la materia. Tal
colapso sería factible, si el Universo (inicialmente estático y extendido)
tuviera límite o si la materia no estuviese distribuida homogéneamente en toda
la extensión del espacio infinito.
Veamos:
Si
el Universo tiene una densidad de masa q, una masa total M y un radio R
infinito, la fuerza gravitacional (para un modelo esférico), estará dada por:
F
= -G x 4/3πqR
Siendo
q > 0 , R ® ¥ ,
y G la constante gravitacional, tenemos:
F
= ¥
El
valor infinito de F supone un tirón suficiente para colapsar el Universo,
siempre y cuando no muestre una jerarquía en la distribución de masa, como se
verá, cuando
q
= a/R.
Si:
q
= a/R y M = 4π
Tenemos
integramos:
M = 4/3π a/R
(R3) = 4/3π a R2
Luego:
para R infinito, como M = 0
y q = 0 , se evita el
colapso.
3.1
La Paradoja de Olbers (1823)
Existe
una contradicción denominada Paradoja de Olbers: si el Universo es
infinito y la densidad de estrellas es uniforme "no debe existir noche,
pero la noche existe".
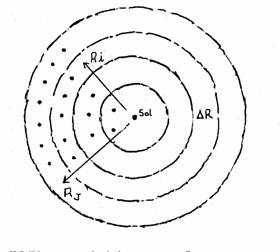
|
Figura
58. Separación de un Universo infinito, en capas esféricas concéntricas con la
Tierra, de radio variable en Ù R.
Se
pueden tomar infinitas capas de Radio R separadas por un espesor ÙR
despreciable. El número de estrellas en cada capa esférica aumenta con el
cuadrado del radio, R2, y la luminosidad de cada capa, vista desde
la Tierra, disminuye en intensidad con el cuadrado del radio, 1/R2.
Luego, si a una distancia R medida desde la Tierra, el número de estrellas para
una capa se compensa con la intensidad de la luz emitida por ellas, el efecto
luminoso de cualquiera de las capas, es el mismo sobre la Tierra. Supone ello
que las infinitas capas se pueden reemplazar por el efecto de infinitas
estrellas equivalentes en la capa primera, con lo cual la Tierra se debe
incinerar.
La
solución a la paradoja se da porque el Universo no es infinito y porque las
capas lejanas hacen menor efecto luminoso que las capas cercanas sobre la
Tierra, debido a la expansión relativa del Universo (efecto Doppler).
3.2
Termodinámica del Universo
El
Universo muestra, desde el punto de vista termodinámico, dos contradicciones:
A.
Desequilibrio termodinámico, pues siendo tan viejo no se esperaría en su fría y
oscura extensión, la presencia de objetos calientes y brillantes. En este caso,
por la segunda Ley de la Termodinámica, la ENTROPIA debe necesariamente
aumentar y ello no está ocurriendo.
B.
La energía que se emite es mayor que la energía absorbida. ¿Qué se hace el Ù
E? ¿Será el que se consume en la expansión? ¿Se convierte en nueva materia para
mantener constante la densidad de galaxias?. En tal caso, el desplazamiento al
rojo puede ser la parte de energía perdida pues, de lo contrario, no se
cumpliría la primera ley de la Termodinámica (conservación de la energía).
3.3
Forma del Universo
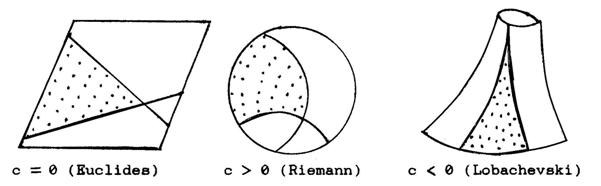
Su
curvatura podría ser cero, positiva o negativa; en cada caso sus propiedades
serían diferentes, como son diferentes los resultados en las geometrías
asociadas a dichas curvaturas:
|
|
para
Euclides: S = 180° A = πR2 P = 2πR
│
para
Riemann: S > 180° A > πR2 P > 2πR
│
para
Lobachevski: S < 180° A < πR2 P < 2πR
│
Figura
59. Universos continuos y bidimensionales. c es la curvatura, S la suma de los
ángulos interiores en un triángulo, A el área de un círculo y P el perímetro de
una circunferencia, de radio R.
Esto
en dos dimensiones, pero el Universo tiene cuatro así: tres espaciales y el
tiempo. Cualquier dimensión es ortogonal con las otras tres (todas lo son entre
sí).
Si
hoy se acepta que el Universo es finito
e ilimitado, por su curvatura positiva (Riemann), es sólo una hipótesis, podría
demandarse una geometría discontinua (no inventada) que explique mejor su forma.
4.
LEY DE HUBBLE
Este
astrónomo toma fotografías de galaxias lejanas. Las más pequeñas y opacas
muestran mayor desplazamiento al rojo que otras más grandes y brillantes con
forma similar. Por la forma el tamaño real de las galaxias debería ser en
promedio igual. Sólo la distancia a esas galaxias explicaría su tamaño y brillo
variables en las fotografías, y sus diferentes corrimientos al rojo,
velocidades radiales explicando un Universo en expansión relativista, que
arrastra las galaxias.
|
|
Figura
60. El Universo se expande arrastrando las galaxias, independientemente del
movimiento propio que tengan ellas. La función de escala del Universo, será el
cociente entre los radios del Universo en dos momentos del tiempo cósmico t.
Esta función podrá crecer o decrecer, según el Universo se expanda o contraiga.
Así
el Universo está en expansión relativista y la constante de expansión de Hubble
(H) es del orden de 65 Km/seg por Mpc (mega parsec). De por medio está la
incertidumbre con respecto a la densidad media actual del Universo. El rango
dentro del cual se encuentra el valor de la constante, será el requerido para
que cada 100.000 millones de años, se expanda entre un 5% y un 10%.
No
obstante por el fenómeno relativista, los cuerpos más lejanos parecen alejarse
a velocidades cada vez mayores, puesto que ellos acumulan los desplazamientos
de los cuerpos celestes intermedios.
El
tejido de expansión del Universo, viajaría a una velocidad cercana a la de la
luz. Más allá, todo viajaría a esa velocidad -cuyo valor es un límite físico-,
y de esa región no nos llegará ningún tipo de información. Por ésta razón, sólo
se habla del Universo observable.
En
el capítulo siguiente, se calculará la edad del Universo, dada por el inverso
de la constante H.
(delta
lamnda)/lamnda= v/C
Siendo
lamnda la frecuencia de la raya espectral original, delta lamnda el
corrimiento de la raya,
En
la estructura del Universo observable se tiene que su densidad es 10-25 g/cm3, su volumen 1078
m3, el radio 15000 millones de años luz y la masa 1052
kg, equivalentes a 1080 nucleones.
|
|
Figura
61. Curvas de velocidad de expansión del Universo. A mayor distancia mayor
velocidad. La mayor de las velocidades es la que alcance el valor de c. La
menor es va = 0, que es la del origen.
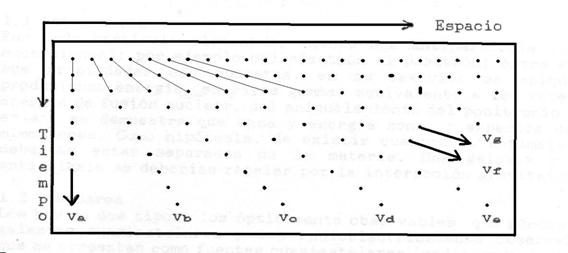
Sumergiéndonos
en el espacio-tiempo
Ahora
pensemos como se verá el Universo en el tiempo, por supuesto en el tiempo
pasado. Para tal efecto deberemos sumergirnos, paso a paso, en las
profundidades del espacio.
Los
cuásares que están a 4000 Mpc, los vemos con una antigüedad de 13000 millones
de años. Ellos se encuentran en el tejido de expansión del Universo. Son tan
antiguos como él mismo.
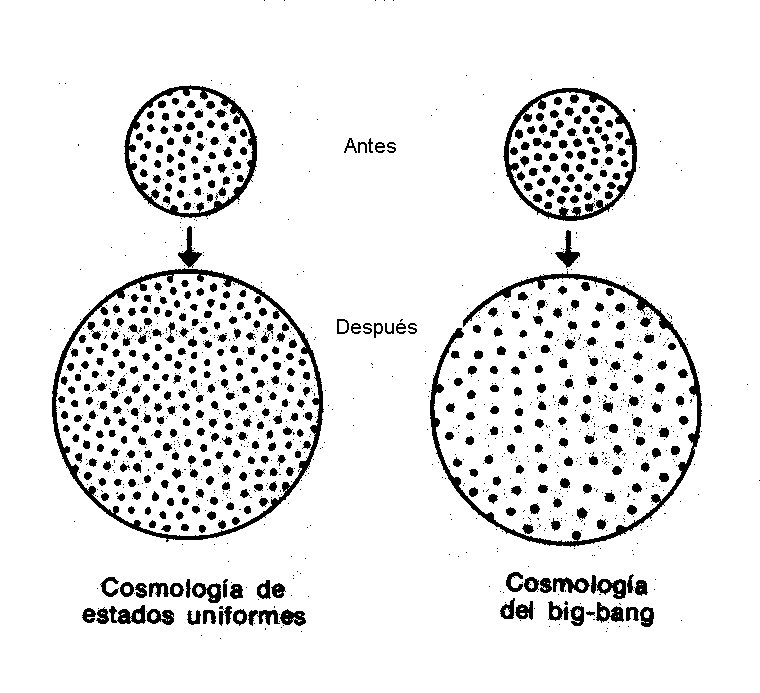
Existen
dos posibilidades: que entre las galaxias (que son próximas a nosotros) y los cuásares
se encuentren, solamente, los objetos estelares azules BSO -entes intermedios
entre cuásares y galaxias-, sin que en la vecindad de nosotros se encuentren cuásares,
ni en los dominios de los cuásares las galaxias. En este primer caso supondríamos
que el Universo evoluciona en el tiempo.
La
segunda posibilidad sería la de tener cuásares, galaxias y objetos BSO,
uniformemente distribuidos en el espacio y el tiempo. Tendríamos entonces cuásares
en medio de galaxias próximas y galaxias en medio de cuásares lejanos,
adicionalmente objetos BSO entre unos y otras. En este caso no habría evidencia
de evolución de la materia a lo largo del tiempo cósmico.