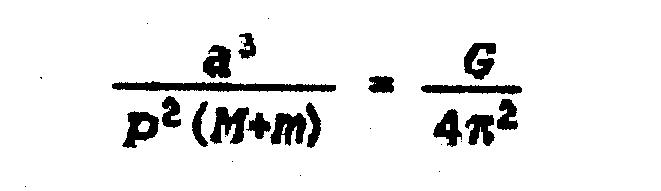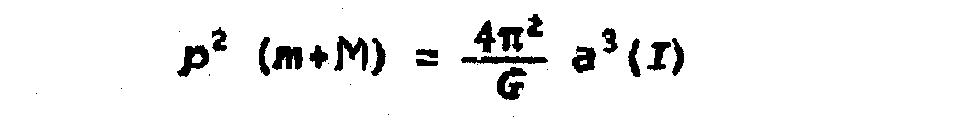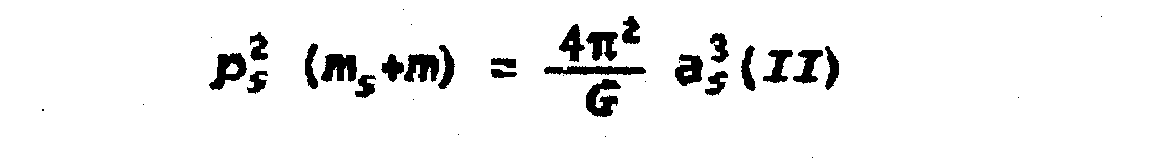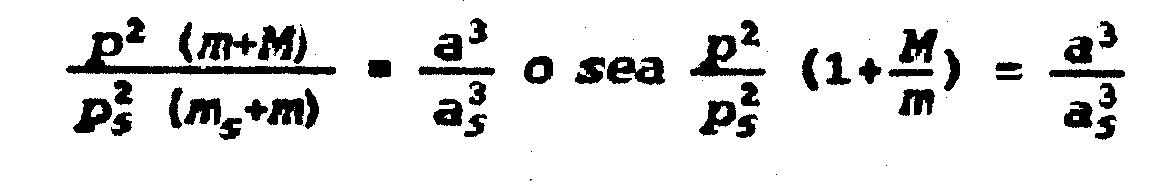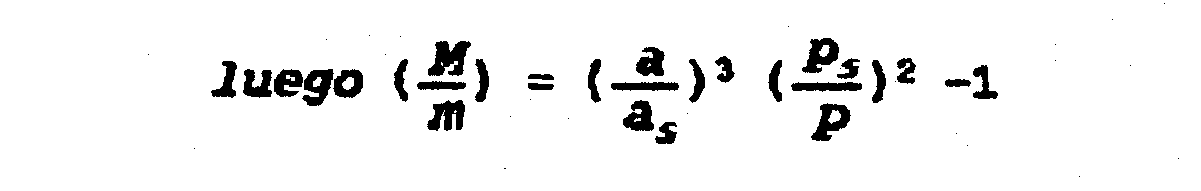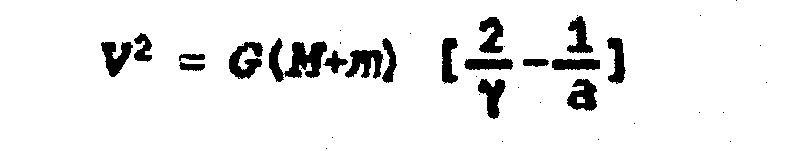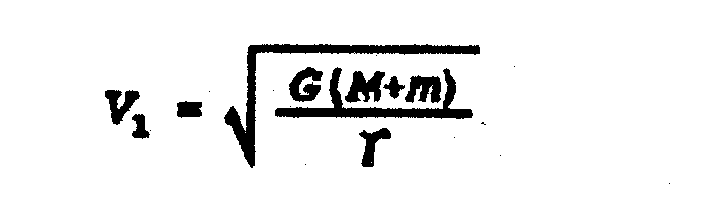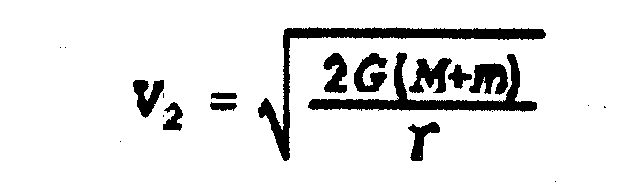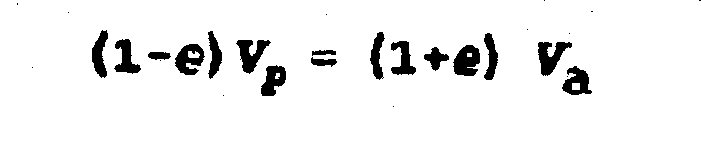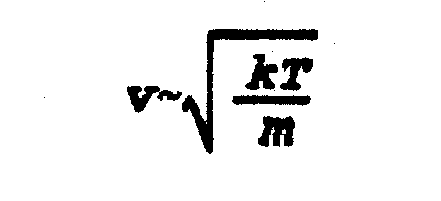Sistema Tierra Luna. Websshots.com

Guía Astronómica Gonzalo Duque-Escobar, P. As. Universidad Nacional de Colombia Manizales, 1992

GUIA Nº 3

  ELEMENTOS DE MECANICA

PLANETARIA

 

 

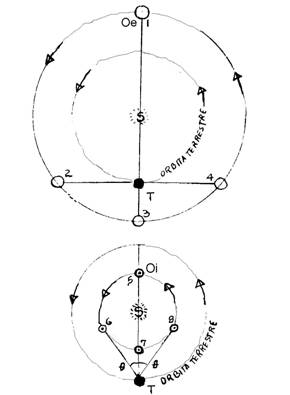
1. POSICIONES DE UN PLANETA INTERIOR Y DE UNO EXTERIOR

 

Tomando el Sol como centro se dibujan las órbitas de tres planetas; sean ellos Venus, Tierra y Marte respectivamente a partir del Sol.

 

Si la traslación de los planetas es retrógrada con relación a la estrella Polar y las velocidades orbitales resultan poco diferentes, los períodos (años) de los planetas difieren y las posiciones de ellos son las siguientes, vistas desde la Tierra y con relación al Sol.

 

Como asunto fundamental, las estrellas parecen fijas o firmes en el cielo o firmamento, mientras los planetas son errantes.

 

Oe = planeta exterior  ( o inferior) Oi = planeta interior    (o superior)  T = Tierra, S = Sol  Planeta exterior: 1 = conjunción 2 = cuadratura Este 3 = oposición 4 = cuadratura Oeste Planeta interior: 5 =conjunción superior 6 = elongación Este 7 =conjunción inferior 8 = elongación Oeste

 

Figura 9. Posiciones para un planeta exterior a la Tierra (arriba) y para un planeta interior a la Tierra (abajo).

Nos preguntamos ahora ¿Cómo diferenciar planetas de estrellas y planetas entre sí?

 

Es importante diferenciar los planetas de las estrellas. Los primeros no titilan, las estrellas sí. Ello se debe a la atmósfera.

 

Por la enorme distancia que nos separa de las estrellas, sólo nos llega de cada una de ellas un rayo de luz. Por los movimientos del aire, ese rayo se desvía intermitentemente y la estrella titila.

 

De los planetas, llegan muchos rayos de luz, simultáneamente, hasta el ojo del observador. Cuando uno de ellos se desvía a causa del aire, otro toma de inmediato su posición.

 

Pero también es importante diferenciar los planetas entre sí. Los planetas interiores no pueden ser vistos a media noche, como ocurre con planetas exteriores, que tienen oposición. Los primeros, según su elongación, serán visibles horas o minutos después del atardecer o antes de la madrugada.

 

El color rojo o anaranjado de Marte y Saturno más intenso en el primero y el color blanco de Venus y Júpiter, contribuye también a la diferenciación del planeta. Pero adicionalmente, las fases y los movimientos que muestre el astro son importantes.

 

Fases de Venus:    A = Creciente   O B = Llena C = Menguante     l D = Nueva

 

 

Figura 10. Cara iluminada de la Tierra, y de un planeta interior, de acuerdo al sistema Tierra-Planeta-Sol.

 

a) Los planetas interiores, como Mercurio y Venus, tienen las cuatro fases de la Luna: como se muestra en la figura 10.

 

 

b) Los planetas exteriores próximos (Marte, Júpiter y Saturno) son visibles y hacen bucles. La figura muestra el movimiento retrógrado de un planeta exterior, como Marte.

  

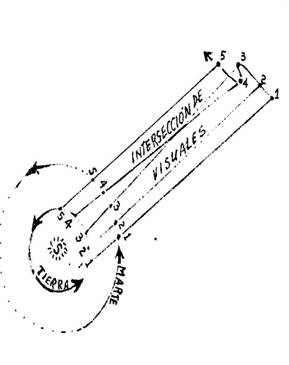
Parte superior: Esfera Celeste sobre la  cual se proyecta la imagen de Marte, si lo vemos desde la Tierra. Como Marte es más lento que la Tierra, su imagen hace bucles. Planeta Marte, año sideral de 687 días. Planeta Tierra, año sideral de 365 días.   Parte inferior: Sol y órbitas de Tierra y Marte, con 5  posiciones sucesivas. Las visuales salen de la Tierra, pasan por Marte y llegan a la Esfera Celeste.

 

Figura 11. Imagen de Marte, que proyectada sobre la esfera celeste, hace un bucle entre las posiciones 3 y 4.

 

2. VALORES l - L EN LAS CONFIGURACIONES DE LOS PLANETAS

 

τ = punto vernal    T = Tierra    S = Sol     P = Planeta observado      l'= TP, longitud  geocéntrica del planeta   l = SP, longitud heliocéntrica del planeta   L= longitud Heliocéntrica de la Tierra

   

Figura 12. Longitudes de un planeta y la Tierra, sea el planeta interior o exterior. A la derecha, de 1 a 4 posiciones de un planeta superior y de 5 a 8 posiciones de un planeta inferior.

 

Conjunción inferior    l - L = 0°

 

Conjunción superior    l - L = 180°

   

Elongación W           l - L = 90° - θ

 

Elongación E           l - L = 270° - θ

 

Conjunción   l - L = 180°

 

Oposición    l - L = 0°

 

Para Mercurio θ = 27° y para Venus θ = 48°

 

3. LEYES DE KEPLER <

 

Johannes Kepler, basado en las posiciones de Marte, que Tycho Brahe observó y midió, publica en 1609 las dos primeras leyes del movimiento planetario y en 1619 la Tercera ley.

 

Estas leyes permiten consolidar el esquema heliocéntrico, mejorar las predicciones astronómicas y dimensionar el tamaño del sistema solar.

 

1. Cada uno de los planetas se mueve siguiendo una órbita en forma de elipse, en uno de cuyos focos se encuentra el Sol.

 

2. Al moverse un planeta, su radio vector (línea planeta Sol) describe iguales áreas en iguales intervalos de tiempo.

 

3. Los cuadrados de los períodos de revolución sidéreos de los planetas, son proporcionales a los cubos de los semiejes mayores de sus órbitas (a los cubos de sus distancias medias al Sol), o sea:  

 

Tercera Ley      a31 /   a32 = p21  /   p22	v = anomalía verdadera r = radio vector del planeta

  

Figura 13. Orbita elíptica de un planeta, con el Sol en uno de sus focos. A la izquierda se ilustra la segunda ley.

 

De acuerdo a la figura anterior, la Línea de los ápsides es  la recta del afelio al perihelio, cuya longitud es 2a, siendo a el semieje mayor de la elipse. Siendo F el foco de la elipse ocupado por el Sol como centro de masa, A el afelio y P el perihelio del planeta, como O es el centro geométrico de la elipse, tenemos:

 

                       AO = OP = a

                        OF = c

                        e = c/a = excentricidad

                           

Definida la excentricidad e, como el cociente entre los valores anteriores, los tipos de órbitas podrán ser:

 

   Orbita parabólica sí    e = 1

 

   Orbita elíptica si        0 < e < 1

 

   Orbita circular si         e = 0

 

También, la distancia máxima entre el Sol y el planeta, AF, y la distancia mínima FP, están dadas por

 

                       AF = a (1 + e)

 

                       FP = a (1 - e)

 

En el segundo miembro de cada ecuación a representa el valor del semieje mayor de la elipse y e su excentricidad.

 

4. ELEMENTOS DE LAS ORBITAS PLANETARIAS

 

Los elementos de una órbita sirven para determinar la órbita de un satélite, un planeta, etc.

 

Supongamos que el plano de una órbita, se describe con relación al plano de la eclíptica. En consecuencia se debe conocer la inclinación de ambos planos, la línea de intersección entre ellos, la geometría de la órbita elíptica y la posición de esa elipse, entre otras variables.

 

A modo de ejemplo, los elementos de la órbita del cometa Halley (órbita número 33 del International Halley Watch) son:

instante de paso por el perihelio 1986 febrero 9, 45862, 

distancia al Sol en el perihelio 0,5871012 UA, 

excentricidad 0,9672750, argumento del perihelio 111°,84652, 

longitud del nodo ascendente 58°,14341,& 

inclinación 162°,23921.

 

Para ilustrar los comentarios veamos la figura siguiente:  

 

Ω = longitud de los nodos NN'  i = inclinación del plano orbital  e = c/a   e = (a-b)/a    a y b = semiejes orbitales    v = anomalía verdadera     r = radio vector de posición    T = paso por el perihelio     t = momento de coordenadas v y r    W = argumento del perihelio

 

Figura 14. Intersección entre un plano orbital y la eclíptica, para describir los elementos de una órbita planetaria.

 

5. ECLIPSES DE SOL Y DE LUNA

Los eclipses de Sol tienen lugar en novilunio; los eclipses de Luna, en plenilunio y cuando la Luna está situada en el plano de la órbita terrestre o en la vecindad inmediata del nodo ascendente o descendente. En el primer caso, la Luna oculta en mayor o menor medida al Sol; en el segundo, la Luna desaparece total o parcialmente en la sombra de la Tierra.

 

Las condiciones anteriores hacen que los eclipses se produzcan separados por medio año aproximadamente. En efecto, si los nodos de la órbita lunar están en las proximidades del equinoccio de primavera y otoño sobre la eclíptica, es de prever que haya eclipses de Sol en la Luna Nueva apareciendo en torno al 21 de marzo y al 23 de septiembre, respectivamente, y eclipse de Luna en la fase de plenilunio que se dé en ese mismo intervalo. Por término medio hay anualmente 2 a 3 eclipses de Sol y de 1 a 5 eclipses de Luna. Ahora bien, como la línea de nodos es retrógrada, se van adelantando los eclipses de año en año, repitiéndose exactamente igual al cabo de unos 18 años.

 

La duración exacta de este período de Saros se puede calcular, si se tienen en cuenta que 223 meses sinódicos equivalen casi exactamente a 242 meses dracónicos: 18 a 10,3216 d frente a 18 a 10,3592 d. La pequeña diferencia de 0,0376 d hace, sin embargo, que los ciclos de Saros de eclipses iguales se desfasen de nuevo al cabo de algunos milenios.

 

5.1. Eclipses de Sol <

En los eclipses de Sol hay que distinguir las siguientes formas:

 

1. Eclipses parciales: en loss cuales la Luna nueva sólo oculta una parte del disco solar. El observador está situado entonces en la penumbra de la Luna.

 

2. Eclipses totales: en loss cuales queda oculto el disco solar entero. El observador se halla en la umbra de la sombra que proyecta la Luna. Dado que esta sombra sobre la superficie terrestre sólo tiene un diámetro máximo de 200 km, los eclipses totales sólo son visibles desde una región muy limitada. Debido al efecto conjunto del movimiento de la Luna alrededor de la Tierra y de la rotación de ésta, la sombra de la Luna se desplaza con una velocidad de unos 28 km /min por encima de la superficie terrestre (en el ecuador) y barre una banda de totalidad (casi siempre de W a E) sobre la cual se va observando sucesivamente un eclipse total de Sol. La totalidad dura un máximo de 8 minutos; en ese intervalo el cielo se oscurece hasta el punto de hacerse visibles muchas estrellas y planetas. Alrededor del disco solar oculto aparece el anillo luminoso de la corona.

 

3. Eclipse anular: en el cual se hace visible un anillo del disco solar. Si la Luna está cerca de su apogeo (a la mayor distancia de la Tierra), entonces el diámetro angular de su disco es tan pequeño que no se produce un eclipse total sino anular.  

 

 

 

Figura 15. Eclipse de Sol. En la zona de umbra el eclipse es total, en la de penumbra es un eclipse parcial.

 

5.2. Eclipses de Luna <

Los eclipses de Luna, a diferencia de los de Sol, son visibles desde una zona geográfica mucho mayor; concretamente desde todo el lado nocturno de la Tierra que tiene la Luna llena sobre el horizonte. La zona de visibilidad es incluso mayor al 50% de la superficie terrestre, debido a que los eclipses de Luna llegan a durar hasta un máximo de 3½ horas.

 

La sombra que proyecta la Tierra aparece algo aclarada y suele mostrar una coloración rojiza. Incluso en un eclipse total de Luna, es raro que la Luna desaparezca del todo. El fenómeno se debe a la atmósfera terrestre: los rayos de Sol que inciden tangencialmente en ella se refractan y penetran en el cono de sombra proyectado por la Tierra, y es la luz rojiza de longitud de onda larga la que pasa con más facilidad. El tipo de coloración y el grado de obscurecimiento en un eclipse de Luna dependen de las condiciones atmosféricas de la Tierra, pero a veces también, del contenido de polvo de la atmósfera, habiéndose observado eclipses oscuros después de erupciones volcánicas.

 

6. LEY DE LA GRAVITACIÓN

 

La ley de la gravitación enunciada por Isaac Newton, dice que todas las masas del Universo se atraen mutuamente con una fuerza F que es proporcional al producto de las dos masas m₁ y m₂ e inversamente proporcional al cuadrado de la distancia r, así:  

F = G m₁ m₂ / r_t²

 

donde G es la constante gravitatoria universal.

 

Para calcular la gravedad en la superficie de la Luna y compararla con la de la Tierra, imaginemos la Tierra o la Luna de forma esférica y despreciemos los efectos de su rotación.

 

La fuerza de la gravedad en la superficie de la Tierra, es g_t, cuyo valor está dado por:

 

g_t = G m_t/r_t²

 

Hemos denominado m_t y r_t a la masa y radio de la Tierra. Además G es la constante de gravitación.

 

El valor de la aceleración g_l en la superficie de la Luna, si su masa y radio son m_l y r_l, esta dado por una expresión análoga:

 

g_l = G m_l/r_l²

 

Dividiendo entre sí ambas ecuaciones se obtiene la relación de las fuerzas de gravedad, al reemplazar numéricamente masas y radios, que para el efecto es seis veces mayor en la Tierra.

 

De la ley gravitatoria se pueden deducir las leyes de Kepler. La tercera, para un planeta de masa m dice:

 

 

 

 Donde M es la masa del Sol y a la distancia Sol-Planeta

Un planeta se haya en una órbita estable cuando no se precipita hacia el Sol, como consecuencia de la fuerza de gravedad, ni sale despedido de la órbita como consecuencia de la fuerza centrífuga.

La fuerza de gravedad del Sol y la fuerza centrífuga tienen que equilibrarse mutuamente.

 

La fuerza centrífuga C  depende de la masa m del planeta, de su velocidad orbital v y del radio de curvatura r de la órbita, es decir, de la distancia planeta- Sol.

C= mv²/r

 

Cálculo de la masa de un planeta con satélite

Tomemos el Sol de masa M, el planeta de masa m y el satélite de masa Ms. Sean los períodos p del planeta y Ps del satélite, y G la constante de gravitación de Newton. Las fórmulas más exactas en la tercera ley, nos permiten decir que:

 

Planeta vrs. Sol:  

 

Satélite vrs. Planeta:

 

 

Dividiendo las ecuaciones I y II tenemos:

 

 

 Hemos dividido por  m y considerado m_s /m despreciable

 

 

:. Con lo cual, como M/m se conoce, sale m.

 

7. ROTACIÓN DE DOS CUERPOS ALREDEDOR DE UN CENTRO DE MASA a

El esquema muestra un sistema doble, conformado por dos soles que se orbitan entre sí. Las dos órbitas están en el mismo plano y los focos de las órbitas deben alinearse y disponerse de tal manera que ambas tengan un foco común en el centro de masa. Los sistemas de tres y más cuerpos presentan varias soluciones, razón por la cual dichos sistemas múltiples resultan indeterminados.

 

Al tratarse de elipses, siendo A₁ y A₂ los semiejes mayores, la distancia entre los dos cuerpos d₁ + d₂ , será el producto entre uno de los semiejes y la razón de las masas X/Y o Y/X según se trate de  A₁ o A_2.

 

En este arreglo geométrico el período de los planetas es el mismo (condición de alineamiento con el centro de masa a), al igual que la excentricidad de las elipses ( por la relación anterior).  

 

masa X . d1 = masa Y . d2       (Ley de Distancias)    d1+d2 = A1.masa X/masa Y   d1+d2 = A2.masa Y/masa X     Areas BCa+bca=constante           (Ley de Areas)

                                       

Figura 16. Dos estrellas girando alrededor de un centro de masa, para ilustrar el problema de dos cuerpos.

 

Si la masa de un cuerpo X resulta insignificante, comparada con la de su compañero Y, como el caso del sistema Luna-Tierra o del sistema Tierra-Sol, el centro de masa coincide prácticamente con la masa Y, y la distancia total (d₁ + d₂) se hace semejante a d₁.

En este caso el segundo cuerpo de gran masa puede considerarse en reposo, como primera aproximación, para que el primero describa una órbita elíptica, cuyo semieje será la suma de los semiejes A₁ + A₂ con el segundo en uno de sus focos, de la manera que se ha ilustrado en las leyes de Kepler.

 

Para el caso de dos cuerpos con masas similares, la órbita es también una elipse cuyo semieje mayor es igual a la suma de los semiejes A₁ + A₂.

 

Ilustraremos el caso del sistema Tierra-Luna, haciendo uso de los siguientes valores para conocer que tan cerca de la Tierra, y lejos de la Luna, se encuentra el centro de masa a:

 

Relación de masas entre la Tierra y la Luna                 mT/mL = 81        (1)

 

Distancia media entre la Tierra y la Luna                    (d_T + d_L)=384400 km (2)

 

Por lo visto en la relación de la Figura anterior           1/81 = d_T/d_L

 

De las dos últimas ecuaciones (1) y (2)                       d_T = 384400 - 81 . d_T

 

Se obtiene de la anterior ecuación una distancia d_T de 4700 km, valor que, comparado del radio de la Tierra de 6378 km, nos dice que el centro de masa a, alrededor del cual orbitan la Luna y la Tierra, queda en el manto de la Tierra y a una profundidad del orden de 1678 km, medidos desde su superficie.

   

8. VELOCIDAD ORBITAL <

 

¿A qué velocidad debe girar la Tierra para mantenerse en órbita?

Si gira muy rápido escapa, si gira muy lento cae al Sol.

 

 

   

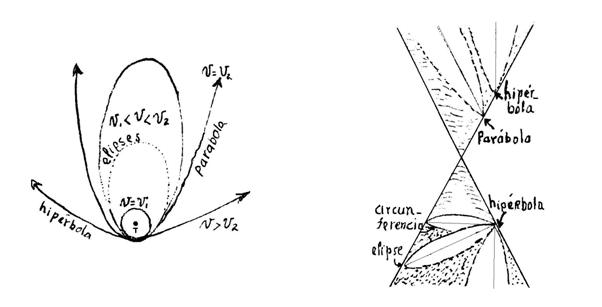
Figura 17. Superficie cónica, que intersecada por un plano, genera las cónicas.

 

Calcularemos V₁ y V₂ que son las velocidades límites para el giro del planeta.

 

Fórmula General

 

Si  r = a  : la trayectoria es circular y se obtiene la primera velocidad de escape, que es

 

 

Si a es infinito : la trayectoria es parabólica y se obtiene la segunda velocidad de escape que es

 

 

Igualmente, en caso de órbita elíptica, la velocidad es variable, pero su valor máximo, en el perihelio, no supera V₂ y su valor mínimo, en el afelio, no resulta inferior a V₁.

 

Llamando a ambas velocidades V_p y V_a respectivamente, en una órbita de excentricidad e, se debe cumplir que:  

 

De la segunda velocidad de escape depende que un cuerpo celeste tenga atmósfera, pues dicho valor se compara con la velocidad térmica de las moléculas de gas dada por la siguiente expresión que involucra la temperatura ambiental T y la masa molecular m:  

 

Mientras la segunda velocidad de escape en la Tierra, es de 11,2 km/s, las velocidades térmicas moleculares de los gases ligeros a la temperatura de 300⁰ K, son: para el hidrógeno, 1,1 km/s y para el helio, 0,8 km/s. Para el oxígeno y el nitrógeno, los valores son del orden de los 0,3km/s.