3. STRUKTURA A VLASTNOSTI PLYNŮ
Molekuly plynu, který je v rovnovážném stavu nemají v určitém okamžiku stejnou rychlost. Známe-li rozdělení molekul podle rychlosti, můžeme vypočítat střední kvadratickou rychlost molekul ze vztahu
Střední kvadratická rychlost vk závisí na termodynamické teplotě T podle vztahu
vk =  (3kT.m0 -1) (3kT.m0 -1)
kde k  1,38.10x-23x J.K -1 je Boltzmannova konstanta a m0 hmotnost molekuly. 1,38.10x-23x J.K -1 je Boltzmannova konstanta a m0 hmotnost molekuly.
Pro střední kinetickou energii E0, kterou má molekula v důsledku neuspořádaného posuvného pohybu, platí
E0 = 0,5m0vk2 = 3/2kT.
Základní rovnice pro tlak ideálního plynu je
p = 1/3NVm00v02.
kde NV je hustota molekul, m0 hmotnost molekuly a vk střední kvadratická rychlost molekul.
Stavovou rovnici ideálního plynu můžeme psát ve tvarech
pV = NkT,
pV = m.Mm -1.RmT,
pV = nRmT,
kde Rm  8,31 J.K -1.mol -1 je molární plynová konstanta. 8,31 J.K -1.mol -1 je molární plynová konstanta.
Při stavové změně ideálního plynu stálé hmotnosti platí
pV.T -1 = konst.
Izotermický děj s ideálním plynem:
T = konst. pV = konst. zákon Boylův - Mariottův
Izochorický děj s ideálním plynem:
V = konst. p.V -1 = konst. zákon Charlesův
Izobarický děj s ideálním plynem:
p = konst. V.T -1 = konst. zákon Gay - Lussacův
Měrná tepelná kapacita plynu při stálém objemu a tlaku cV a cp je definována vztahy
cV = QV.(m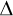 T) -1; cp = Qp(m T) -1; cp = Qp(m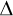 T) -1 T) -1.
Pro adiabatický děj s ideálním plynem (Q = 0) platí Poissonův zákon
pVx = konst.,
kde KAX = cp.cV -1 je Poissonova konstanta.
Z Poissonova zákona a ze stasvové rovnice lze pro adiabatický děj s ideálním plynem odvodit vztah
T1V1 x-1 = T2V2 x-1.
|



