東京工業大学大学院社会理工学研究科
人間行動システム専攻人間開発科学講座 松田研究室 参照 江本 理恵(人間行動システム専攻博士3年)
情報通信ネットワークを活用した情報の収集・発信
模擬授業用テキスト
1.情報とその表現方法
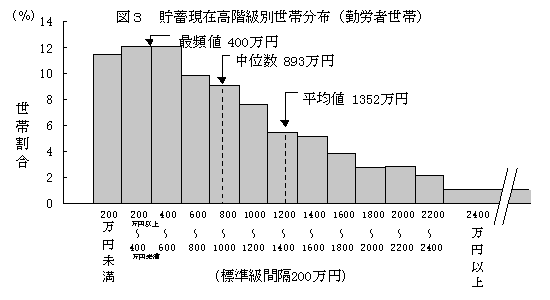
「日本国民の平均貯蓄高は1,352万円!」
B新聞:「日本の国民の平均的貯蓄高は400万円!」
C新聞:「日本の国民の平均的貯蓄高は893万円!」
(1)平均値私たちにとって、一番身近なのがこの平均値でしょう。平均といった場合、たいていは算術平均のことをさし、すべての値を足して、その値の数で割ること(1/n*(x1+x2+・・・+xn)で導出します。ヒストグラムから平均値をもとめる場合、元の値をその測定が属する階級の中心値でおきかえて、平均値を出します。今回の場合、調査した世帯すべての貯蓄高を足して、世帯数で割ったものが平均値になります。 (2)最頻値最大の度数を持つ測定値のことをさします。一番高い度数を持つ柱の階級の中心値をとります。今回の場合、度数が最大になるのは、200万以上〜400万未満、400万以上〜600万未満の2つの階級なので、その2つの柱の中心値をとって、400万が最頻値となります。 (3)中央値測定値を大きさの順にならべたとき、ちょうど中央にくる測定値を、中央値として定義します。中央値をとると、この値よりも大きな値と小さな値がちょうど同数あることになります。今回の場合、中央値の貯蓄高よりも貯蓄の多い世帯と少ない世帯が同じ世帯数になります。 |
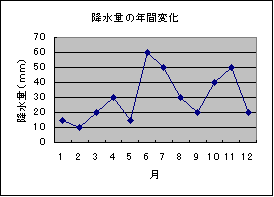
コラムある地域の1年間の降雨量のグラフを、縦軸の取り方をかえてみました。同じデータですが、やはり違った印象を与えます。このように、情報を発信する側で、ある程度の意図をもって情報を表現することが可能なのです。 | |
|

|
|
よって、情報を受け取る側の私たちも、発信されたものをそのまま受け入れるのではなく、どのような意図をもって、どのような情報が発信されているのかを意識する必要があるのです。 | |
実習1インターネットを利用して、複数の新聞を検索し、同じニュースをどのように報じているかを比べてみましょう。
実習2実習1で検索した記事の中に、同じ出来事を、違うものと思える表現をしているものがないかを調べてみましょう。 |
*脚注*
1)ヒストグラム
2)度数分布
3)調和平均
4)幾何平均