|
Gleichgewichtstemperatur im Strahlungsfeld der Sonne |
|
Gleichgewichtstemperatur im Strahlungsfeld der Sonne |
von P. Krahmer
|
Stefan- Boltzmann Gesetz |
sigma = 5.6703 * 10^-8 W / ( m^2 *K^4) Stefan-
Boltzmann- Konstante
A = abstrahlende Fläche, emitting Area
T = Strahlertemperatur
in K (Grad Kelvin)
eps(e) = Emissionsfaktor ( 100% für Schwarzen Körper (blackbody) - 0% für totale
Isolation )
eps(r) = Remissionsfaktor ( 100% für Schwarzen Körper (blackbody) - 0%
totale Reflektion)
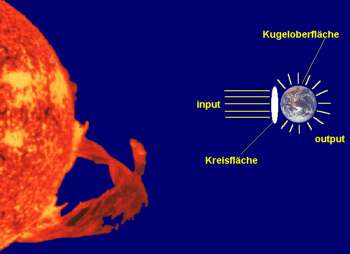 |
Für rotierende kugelförmige Objekte gilt : Solarleistungseinfall = Solarintensität mal Wirkungsquerschnitt oder P(in) = S*A1= S*pi*R^2 mit S=S0/r^2 falls r in AU Abgestrahlte Leistung oder P(out) = A*SE = 4*pi*R^2 * sigma * T^4 über Kugeloberfläche Oberflächenstruktur moduliert diese Leistungen: Im thermischen Gleichgewicht gilt: dann eps(r)*P(in) = eps(e)*P(out) eps(r) * S*pi*R^2 = eps(e)*4*pi*R^2*sigma*T^4 oder T =( eps(r)/eps(e)*S/4/sigma)^0.25 |
Da Stefan-Boltzmann streng nur für schwarze Körper gilt, aber über alle
Wellenlängen summiert, sollte
eps(e)=eps(r)=100% gelten. Es ist ja geradezu widersinnig einem Schwarzen Körper
Weisskörpereigenschaft (Albedo) zuzuschreiben. Dies wird aber dennoch häufig
praktiziert ( (1-A)*S usw.). Um die Richtung von Temperaturänderungen zu klären
kann mit eps=70% für die Erde und eps=93% für den Mond gerechnet werden.
be carefully with Albedo (white Body) as a property of Black Body (T^4 over all
wavelength) !!!
Climatology is no Quantum Mechanics with strange laws.
Strahlungsgesetz- Sonnenstrahlung, Erdtemperatur berechnen
relevante Seiten:
A Simple Greenhouse Climate Model JAVA interaktiv by Steve
Ackerman and Tom Whittaker
Schwarzkörperstrahlung
Nasa Seite
Pre-lab: Stellar Spectra
The Inverse Square Law
Sternspektren
Applications of the Planck Radiation Formula
|
|
|
|
|
|
|
|
|